3.2. Скорости точек твердого тела при плоском движении

3.2.1. Метод полюса

Н а рис.3.4 представлено положение плоской фигуры S и ее отрезка PM в неподвижной системе координат OXYZ, Для произвольного момента времени справедливо векторное равенство:

(3.3)

При движении плоской фигуры векторы и изменяются и по модулю, и по Рис.3.4 направлению, вектор же изменяется только по направлению, так как его модуль равен для твердого тела расстоянию между точками P и M. Продифференцировав по времени равенство (3.3), полуим:

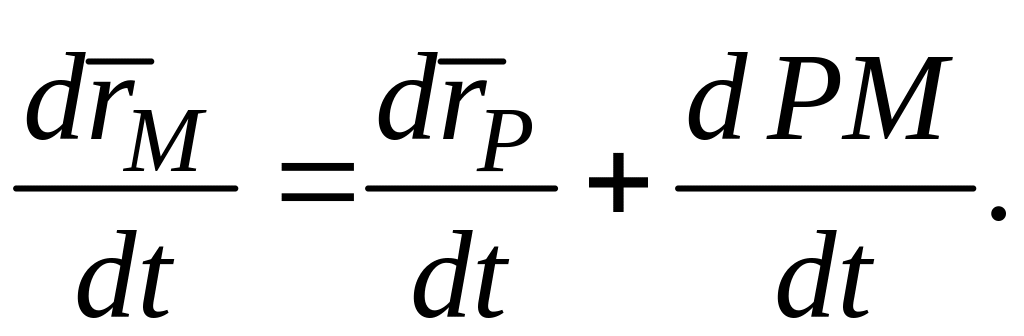
Обозначив 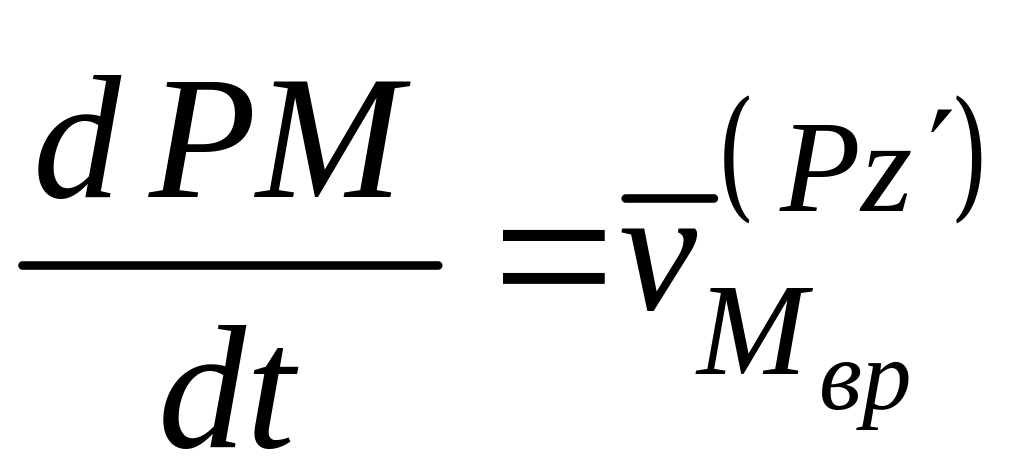и назвав скоростью точки M тела вращении его вокруг оси Pz’, проходящей через полюс P перпендикулярно плоскости плоской фигуры, получим

(3.4)

Рассмотрим вектор . Поскольку вектор  вектор постоянного модуля, то = , где  единичный вектор, лежащий в плоскости фигуры, перпендикулярный и направленный против хода часовой стрелки. Тогда вектор лежит в плоскости фигуры, перпендикулярен отрезку PM, соединяющему точку M с полюсом P, и направлен в сторону вращения плоской фигуры вокруг оси Pz’ (см.рис.3.4).

Модуль вектора определяется как:

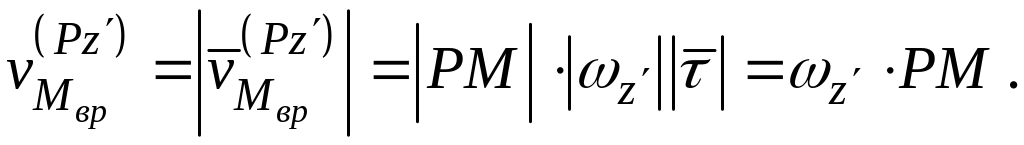(3.5)

Применив векторную формулу Эйлера (2.14), определяющую вектор скорости точки тела, вращающегося вокруг оси, равный векторному произведению вектора угловой скорости тела на радиус-вектор точки относительно какой-либо точки, лежащей на оси вращения тела:

можно представить выражение (3.5) в векторной форме:

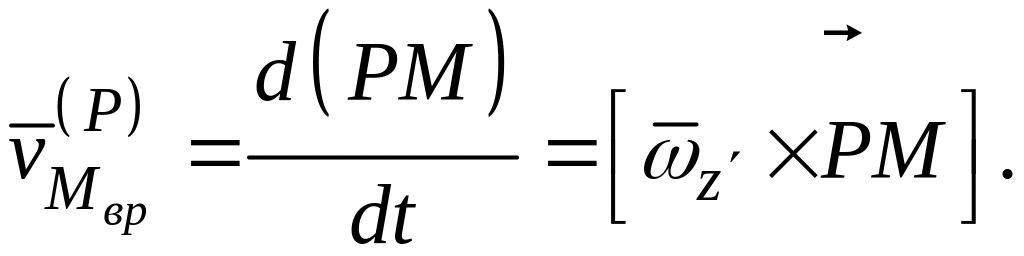
Окончательно имеем выражение для определения скоростей точек плоской фигуры методом полюса:

(3.6)

Таким образом, скорость любой точки плоской фигуры при ее плоском движении по методу полюса равна векторной сумме скорости полюса, построенной при рассматриваемой точке M, и скорости данной точки при вращении фигуры вокруг оси Pz^’, проходящей через полюс перпендикулярно плоскости плоской фигуры.

3.2.2. Метод мгновенного центра скоростей и определение

с его помощью скоростей точек плоской фигуры

Мгновенным центром скоростей называется точка Рис.3.5плоской фигуры, скорость которой в данный момент времени равна нулю. Найдем эту тоску, обозначив ее . Пусть в данный момент времени скорость точки P, принятой за полюс, равна и фигура S вращается с угловой cкоростью Проведем прямую РNH, перпендикулярную вектору , в направлении вращения (см. рис.3.5), отложим на этой прямой отрезок P = и определим скорость полученной точки , выбрав за полюс точку P:

Отсюда следует, что векторы и должны быть равны по модулю и противоположны по направлению. Так как вектор перпендикулярен отрезку P , то прямая, на которой должна находиться точка , перпендикулярна вектору . Чтобы выполнялось условие

=  , точка должна находится на прямой PNH. Поскольку 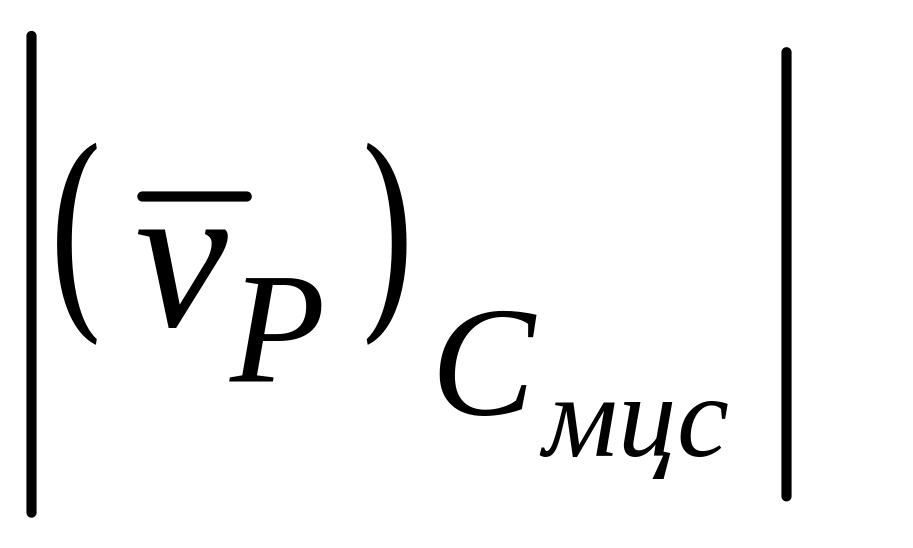= 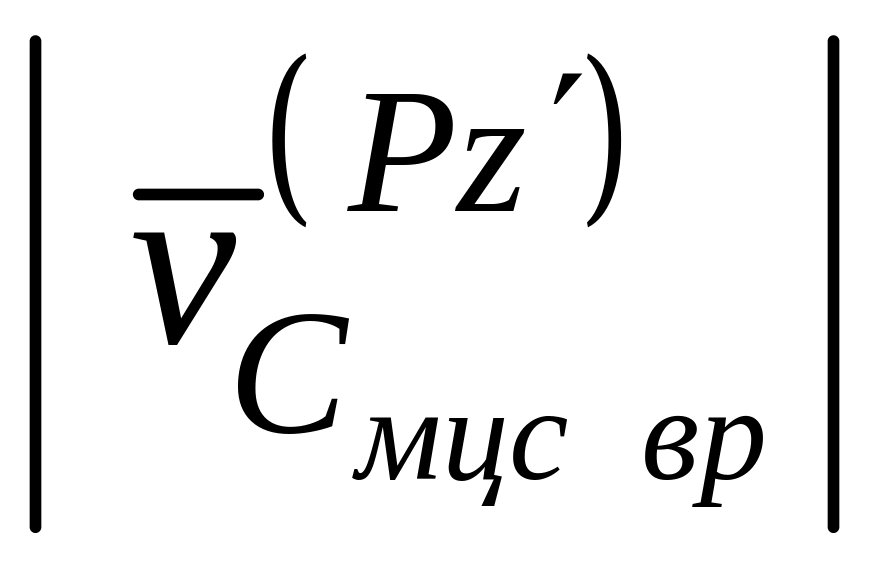, а , мгновенный радиус (расстояние от точки до мгновенного центра скоростей ) будет равен: P = .

Таким образом, приняв за полюс плоской фигуры S точку , можно определить скорость любой точки (пусть точки M) по Рис.3.5 формуле:

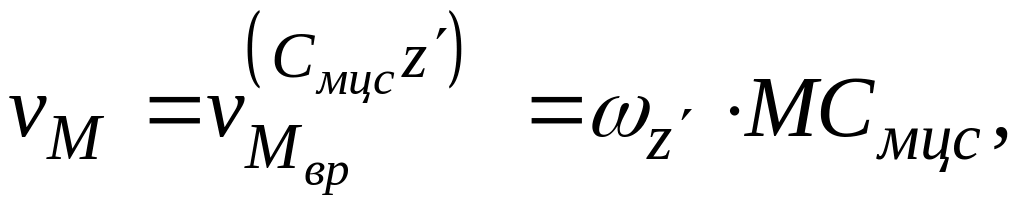(3.7)

где  расстояние от точки M до мгновенного центра скоростей . Вектор перпендикулярен отрезку и направлен в сторону вращения фигуры вокруг оси , проходящей через z’, а его модуль пропорционален мгновенному радиусу = .

Таким образом, скорости точек плоской фигуры в данный момент времени вычисляются так же, как если бы фигура вращалась вокруг оси, проходящей через z’ перпендикулярно плоскости плоской фигуры и плоскости движения, с той же угловой скоростью .

Метод МЦС значительно упрощает определение скоростей точек твердого тела при плоском движении. Поэтому важно уметь определять положение МЦС, т.е. точки .