1. Графопостроитель ху Graph

Назначение:

Строит график одного сигнала в функции другого (график вида Y(X)).

Параметры:

x-min – Минимальное значение сигнала по оси X.

x-max – Максимальное значение сигнала по оси X

y-min – Минимальное значение сигнала по оси Y.

y-max – Максимальное значение сигнала по оси Y

Sample time – шаг модельного времени.

Блок имеет два входа. Верхний вход предназначен для подачи сигнала, который является аргументом (X), нижний – для подачи значений функции (Y).

На рис. 5.2, в качестве примера использования графопостроителя, показано построение фазовой траектории колебательного звена.

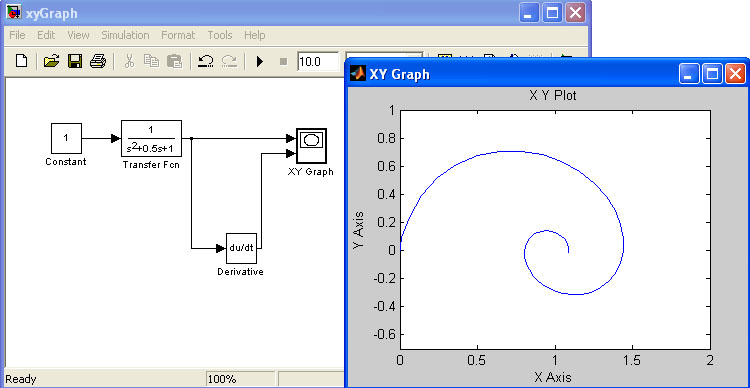
Рис. 5.2

Constant – из Commonly Used Blocks

Чтобы установить необходимые параметры блока необходимо дважды щелкнуть на блоке, в параметрах задать значение константы =1.

Transfer Fcn – Continuous. Представляет собой отношение степенных полиномов. В параметрах для нашего случая необходимо задать числитель: Numerator – [1], и знаменатель: Denominator – [1 0.5 1].

Derivative - Continuous. Блок вычисляет значение производной.

XY Graph – Sinks. Вывод результата на график в виде зависимости X от Y.

2. Блок алгебраического контура Algebraic Constraint

Назначение:

Выполняет поиск корней алгебраических уравнений.

Параметры:

Initial guess – Начальное значение выходного сигнала.

Блок находит такое значение выходного сигнала, при котором значение входного сигнала становится равным нулю. При этом входной сигнал должен быть прямо или опосредованно связан с входным сигналом.

На рис. 5.3 показан пример решения системы нелинейных уравнений вида:

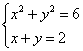
Поскольку данная система уравнений имеет два решения, то начальные значения блоков Algebraic Constraint заданы в виде векторов. Для первого (верхнего) блока начальное значение задано вектором [1 -1], а для второго (нижнего) блока – вектором [-1 1].

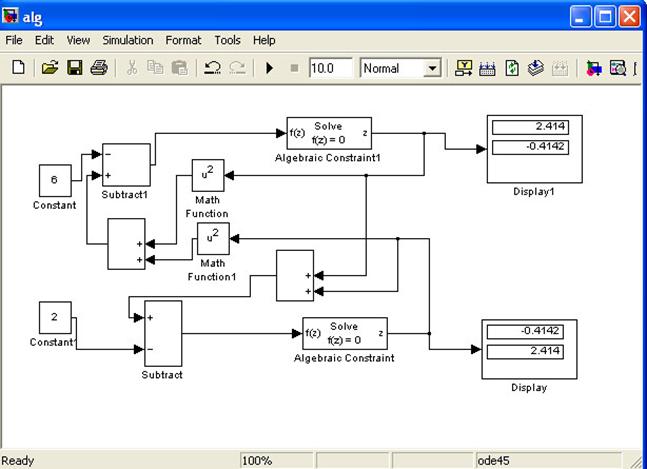
Рис. 5.3

Рассмотрим блоки, которые не использовались в предыдущем примере.

Subtract – Math Operations. В параметрах в окошке List of Signs надо поставить те операции, которые необходимы( - +).

Math Function - Math Operations. В параметрах в окошке Function надо выбрать square( чтобы был квадрат значения).

Algebraic Constant - Math Operations. В параметрах в окошке Initial guess задать начальное значение вектором [1 -1] или [-1 1].

Display – Sinks. Выводит результат.

3. Разработка структурной модели и ее исследование.

1. Задание:

Спроектировать систему регулирования температуры электрической печи сопротивления со следующими параметрами:

постоянная времени печи с;

температура печи ;

точность регулирования .

3.1.1. Составить функциональную схему системы регулирования температуры.

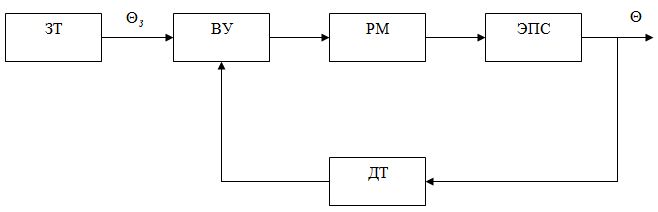
ЗТ – задатчик температуры;

ВУ – вычислительное устройство;

РМ – регулятор мощности;

ЭПС – электрическая печь сопротивления (ОУ – объект управления);

ДТ – датчик температуры (ДОС – датчик обратной связи)

3.1.2. Определить передаточную функцию печи сопротивления и требуемую мощность регулятора мощности, приняв коэффициент передачи печи .

Рассмотрим воздействия, действующие на идентифицируемый объект (ЭПС):

- входная величина (мощность, поступающая в печь), Вт

- выходная величина (температура печи),

- возмущающее воздействие (изменение теплоотдачи),

Можно записать

, где (*)

- мощность, идущая на нагрев;

- мощность тепловых потерь;

- мощность, поступающая в печь и покрывающая две первые составляющие

Совершим преобразование Лапласа над левой и правой частями дифференциального уравнения (*):

В пренебрежении температурными зависимостями и получим:

- постоянная времени печи;

- коэффициент передачи печи

Тогда

Передаточная функция печи сопротивления

Требуемую мощность регулятора мощности определим из установившегося режима, когда . Поскольку коэффициент передачи печи , поэтому требуемая мощность регулятора мощности, в нашем случае, численно равна температуре печи:

Вт.

3.1.3. Выбрать элементы системы регулирования температуры и определить их передаточные функции.

а. Регулятор мощности

В качестве регулятора мощности будем использовать тиристорный регулятор напряжения (мощности). Поскольку в нашем случае речь идет об использовании тиристорного регулятора напряжения для инерционного объекта (ЭПС), то можно пренебречь инерционностью регулятора и считать его безынерционным звеном.

Максимальную мощность регулятора мощности определим из условия её двукратного превышения над требуемой, т.е. из условия , где - коэффициент передачи регулятора мощности.

Тогда передаточная функция регулятора мощности

А сам регулятор мощности представляем в виде:

Максимальная мощность регулятора мощности Вт.

б. Датчик температуры.

В качестве датчика температуры будем использовать хромель-алюмелевую термопару типа ТХА-VIII со следующими техническими характеристиками:

Пределы измерения: 0 1000

Термо-эдс: 0 41.32 мВ

Тепловая постоянная времени с

Примем коэффициент передачи датчика температуры , тогда передаточная функция датчика температуры (термопары):

3.1.4. Составить структурную схему системы регулирования температуры с П-регулятором.

3.1.5. По заданному значению точности определить требуемый коэффициент усиления системы регулирования.

Ошибка по управляющему воздействию

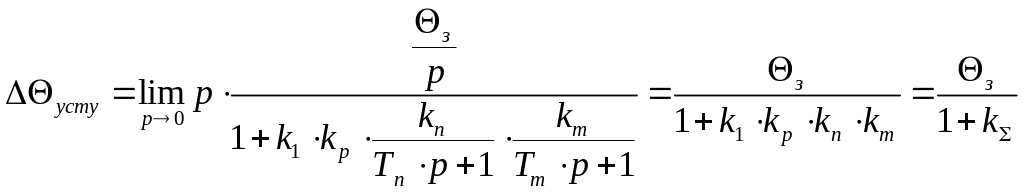, где

- суммарный коэффициент усиления системы регулирования

По условию температура печи

По заданному значению точности определим величину статической ошибки регулирования по управляющему воздействию:

Тогда требуемое значение суммарного коэффициента усиления системы регулирования

Отсюда коэффициент передачи П-регулятора

Проверим это с использованием средств SIMULINK:

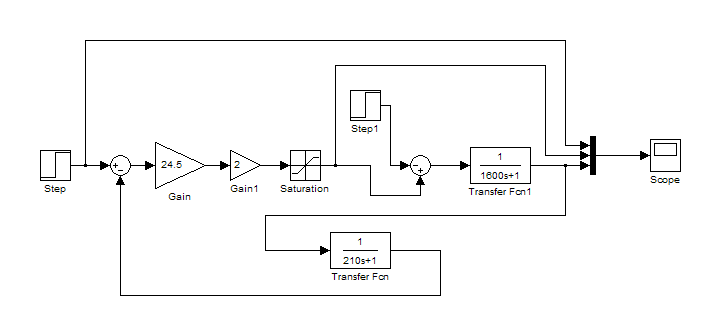
При и получить в Simulink изменение температуры на выходе печи во времени .

Убедиться, что статическая ошибка регулирования по управляющему воздействию .

Ошибка по возмущающему воздействию

Пусть величина статической ошибки регулирования по возмущающему воздействию .

Пусть величина возмущающего воздействия Вт.

Тогда требуемое значение суммарного коэффициента усиления системы регулирования

Отсюда коэффициент передачи П-регулятора

Проверить это с использованием средств SIMULINK.

При и Вт получить изменение температуры на выходе печи во времени .

Убедиться, что статическая ошибка регулирования по возмущающему воздействию .

При одновременном действии управляющего и возмущающего воздействий ( , Вт) величина статической ошибки регулирования

Проверить это с использованием средств SIMULINK.

При и Вт получить изменение температуры на выходе печи во времени .

Убедиться, что статическая ошибка регулирования .

3.1.6. Рассчитать и построить зависимость статической ошибки регулирования от возмущающего воздействия, изменяющегося в диапазоне от 0 до 1 (в относительных величинах).

Зависимость статической ошибки регулирования от возмущающего воздействия

, где , Вт

Полученную зависимость постройте в любом из известных пакетов: Excel, MathCAD или MATLAB.

3.1.7. Проверить систему на устойчивость.

Передаточная функция разомкнутой системы

Передаточная функция замкнутой системы по каналу задания

Передаточная функция замкнутой системы по каналу возмущения

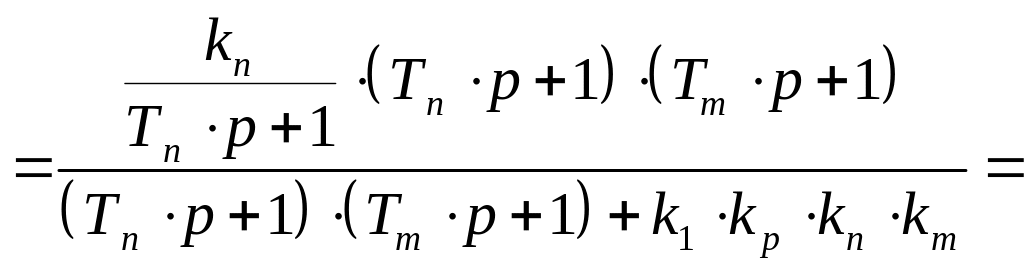
Оценим устойчивость замкнутой системы регулирования, используя алгебраический критерий Гурвица:

Характеристический полином замкнутой системы

Коэффициенты характеристического полинома замкнутой системы:

Условием устойчивости системы второго порядка является положительность коэффициентов её характеристического полинома, следовательно, исследуемая замкнутая система является устойчивой.

Теперь оцените устойчивость исследуемой системы, используя частотный критерий устойчивости Найквиста:

Постройте амплитудно-фазовую характеристику (АФХ) разомкнутой системы (годограф Найквиста) в MathCAD или в MATLAB/Simulink:

Согласно критерию Найквиста, если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал точку комплексной плоскости с координатами (-1; j0).

В нашем случае разомкнутая система устойчива, поскольку корни её характеристического полинома отрицательны, а годограф разомкнутой системы не охватывает точку с координатами (-1; j0), поэтому замкнутая система является устойчивой. Убедитесь в этом, построив годограф.

3.1.8. Рассчитать и построить переходную функцию системы регулирования с П-регулятором для задающего и возмущающего воздействий. Воздействия принимать в диапазоне от 0.5 до 1 (в относительных величинах).

Переходная функция системы регулирования с П-регулятором для задающего воздействия

С использованием средств MathCAD получить выражение для переходной функции системы регулирования с П-регулятором для задающего воздействия и построить ее:

Проверить это с использованием средств SIMULINK.

Статическая ошибка регулирования в обоих случаях одинакова и составляет ( ), однако вид переходных характеристик несколько различается, что объясняется наличием в реальной системе ограничения по мощности регулятора напряжения, используемого в системе регулирования температуры печи сопротивления.

Переходная функция системы регулирования с П-регулятором для возмущающего воздействия

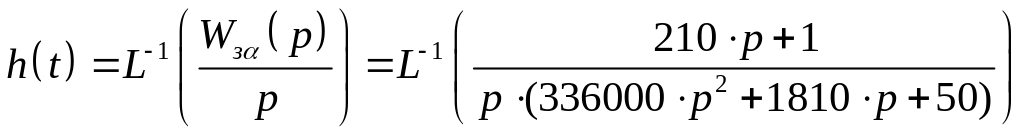
С использованием средств MathCAD получить выражение для переходной функции системы регулирования с П-регулятором для возмущающего воздействия и построить ее:

Проверить это с использованием средств SIMULINK.

Построить в SIMULINK переходную функцию системы регулирования с П-регулятором для задающего воздействия .

Построить в SIMULINK переходную функцию системы регулирования с П-регулятором для возмущающего воздействия Вт.

3.1.9. Провести синтез системы регулирования температуры электрической печи сопротивления, выбрав вид и параметры последовательного корректирующего звена, обеспечивающего перерегулирование не более 0.01 от установившегося значения.

Синтез системы регулирования температуры электрической печи сопротивления будем проводить исходя из того, что перерегулирование .

В качестве последовательного корректирующего звена возьмем ПИД-звено со следующими параметрами: , , .

Пусть .

Проверим в SIMULINK, обеспечивает ли такое звено перерегулирование не более 0.01 от установившегося значения ( ):

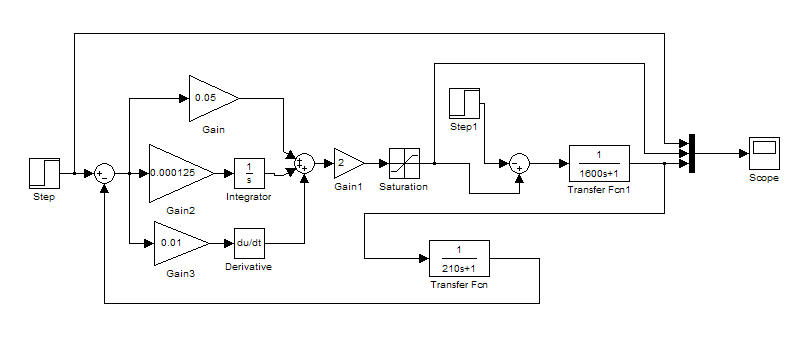
Получим следующие временные зависимости:

В данном случае перерегулирование .

3.1.10. Для рассчитанных параметров корректирующего звена построить переходные функции при изменении задающего и возмущающего воздействий отдельно для каждой составляющей закона регулирования и при использовании всех выбранных составляющих закона регулирования.

3.1.11. Выводы.

Исходная система регулирования температуры электрической печи сопротивления является статической системой (системой автоматического управления с астатизмом 0-го порядка), поэтому отработка системой постоянных входных сигналов осуществляется с конечной статической ошибкой. При этом величина суммарной статической ошибки системы складывается из ошибки по управляющему воздействию и ошибки по возмущающему воздействию. Каждая из этих составляющих, в свою очередь, прямопропорциональна величине самого воздействия и обратнопропорциональна величине суммарного коэффициента усиления системы регулирования. Таким образом, вводя в систему регулирования П-регулятор и увеличивая его коэффициент передачи ( ), мы добиваемся уменьшения величины статической ошибки системы.

Увеличение коэффициента передачи П-регулятора не ведет к потере данной системой устойчивости, поскольку годограф разомкнутой системы (годограф Найквиста) не пересекает мнимую ось в её отрицательной части, а лишь стремится с увеличением частоты к началу координат под углом . Уменьшение статической ошибки с увеличением коэффициента ограничивается лишь максимальной мощностью регулятора напряжения, используемого в данной системе регулирования в качестве исполнительного элемента.

Эффективным способом уменьшения величины перерегулирования и времени переходного процесса является последовательная коррекция, заключающаяся во включении в прямую цепь перед регулятором мощности ПИД-звена с определенными параметрами. При этом система регулирования становится астатической с астатизмом 1-го порядка, поэтому статические ошибки системы, как по управляющему воздействию, так и по возмущающему, будут равны 0. Подбором же самих коэффициентов в законе регулирования можно добиться требуемого характера протекания процесса, а также обеспечить то или иное быстродействие системы регулирования.