Литература

1. Информатика: базовый курс. / Под ред. С.В. Симоновича. – М.: Питер, 2002. – 640 с.

Лабораторная работа № 3. Средства автоматизации научно-исследовательских работ. Среда mathcad. Часть II.

Задание 1. Анализ результата эксперимента

Задача. К пружине последовательно подвешивали грузы массой 1, 2, 3, ... , 20 кг. В результате получен список величин удлинения пружины (в миллиметрах). Определить основные статистические параметры полученного набора измерений. Рассчитать жесткость пружины и массу узла крепления груза к пружине, воспользовавшись методом наименьших квадратов.

Масса, кг	1	2	3	4	5	6	7	8	9	10
Растяжение, мм	3,4	6,8	9,1	12,2	13,4	17,2	22,1	24,2	27,8	29,5

Масса, кг	11	12	13	14	15	16	17	18	19	20
Растяжение, мм	31,7	37,6	39,5	42,8	45,5	46,5	52,1	52,4	56,6	62,4

Математическая постановка. Для решения этой задачи достаточно использовать стандартные средства статистических вычислений, имеющиеся в MathCad. Теоретически растяжение пружины определяется законом Гука

,

где k – жесткость пружины;

m – масса груза;

m₀ – масса крепления;

g – ускорение свободного падения.

Экспериментальная зависимость x(m) аппроксимируется прямой линией . Коэффициенты a и b определяются статистическими методами. Сопоставляя закон Гука и аппроксимирующую зависимость, можно записать

, .

Инструкция по выполнению.

1. Запустите MathCad.

2. Введите таблицу экспериментальных данных в виде матрицы с двумя столбцами, первый из которых содержит массу грузов, второй – величину растяжения пружины. Назовите матрицу data.

3. Определите количество точек в наборах экспериментальных данных с помощью функции rows.

n:=rows(data)

4. Вычислите среднее растяжение пружины в ходе эксперимента с помощью функции mean.

data^<1> означает второй столбец матрицы data (строки и столбцы нумеруются начиная с нулевого номера). Для ввода номера столбца воспользуйтесь соответствующей кнопкой на панели инструментов Matrix (Матрица).

5. Вычислите медиану значений растяжения пружины при помощи функции median(Y).

6. Вычислите среднеквадратичное отклонение и дисперсию (квадрат среднеквадратичного отклонения) величины растяжения пружины при помощи функций stdev(Y) и stdev(Y)² соответственно.

7. Определите коэффициенты линейного уравнения, дающие наилучшее линейное приближение для наших наборов данных. Для определения коэффициентов используется метод наименьших квадратов. Функция slope позволяет вычислить угловой коэффициент прямой, а функция intersept – свободный член.

X:=data^<0>

b:=intercept(X,Y)

a:=slope(X,Y)

8. Определите жесткость пружины и массу узла крепления в соответствии с формулами, полученными при математической постановке задачи.

9. Сохраните документ для использования в следующем упражнении.

• Мы научились применять функции статистического анализа данных. MathCad содержит и другие функции аналогичного назначения, позволяющие интерполировать, экстраполировать и сглаживать данные.

Задание 2. Построение графиков

Задача. Используя результат предыдущей задачи, построить графики экспериментальной и аппроксимирующей зависимостей растяжения пружины от массы груза. Построить также график, демонстрирующий отклонение экспериментальных данных от аппроксимирующей прямой.

Математическая постановка. Для построения графика можно использовать функцию, заданную набором данных или формулой.

Инструкция по выполнению.

3. Запустите MathCad.

4. Загрузите документ, созданный в предыдущем упражнении.

5. Переместите точку ввода в нижнюю часть документа.

6. Запишите формулу функции r(X) для определения координат точек, лежащих на аппроксимирующей прямой. Коэффициенты уравнения этой прямой были получены в предыдущем упражнении.

r(X):=aX+b

Напомним, что как X задан первый столбец матрицы экспериментальных данных.

7. Вызовите панель инструментов Graph (График), нажав клавишу [ @ ], и на панели щелкните по кнопке X-Y Plot (Декартовы координаты). Вместо этого можно воспользоваться командой Insert > Graph > X-Y Plot. В документе появится область для создания графика.

8. Вместо заполнителя (черного квадратика) в нижней части области построения графика укажите в качестве независимой переменной первый столбец матрицы экспериментальных данных (X или data^<0>).

9. Вместо заполнителя слева от графика укажите, что по оси ординат должны откладываться значения второго столбца матрицы экспериментальных данных (data^<1>) и функции, определенной в п. 4 (r(X)). В качестве разделителя используется запятая. Диапазон значений для координатных осей выбирается MathCad автоматически. Щелкните за пределами области построения, чтобы построить график.

10. Чтобы изменить вид автоматически построенного графика, дважды щелкните внутри его области. Откроется диалоговое окно Formatting Currently Selected X-Y Plot (Форматирование графика в декартовых координатах) (рис. 3.1).

Рис. 3.1. Задание способа отображения линий графика

Откройте вкладку Traces (Кривые), первая запись в списке на этой вкладке соответствует первой отображенной кривой, и т.д. Для изменения записи используются поля под списком.

11. Под столбцом Legend Label (Подпись) введите название графика.

12. В раскрывающемся списке под столбцом Symbol (Маркер) выберите способ обозначения для отдельных точек.

13. Под столбцом Type (Вид линии) укажите, что необходимо обозначить отдельные точки (points), а не провести непрерывную линию.

14. Выберите в списке вторую кривую и настройте ее отображение по своему вкусу.

15. Установите флажок Hide Arguments (Скрыть параметры), чтобы не отображать названия осей.

16. Сбросьте флажок Hide Legend (Скрыть подписи), чтобы включить отображение заданных в пп. 9, 12 подписей кривых.

17. В поле Title (Заголовок) на вкладке Labels (Надписи) задайте название графика (Линейное приближение) и включите режим отображения названия: установите флажок Show Title (Показать заголовок).

18. Постройте график, на котором отображалась бы величина отклонения точек от линии приближения (b+aXY). Отформатируйте его, используя те же средства, что и в предыдущем случае.

• Заголовок и подписи, использующие буквы кириллицы, могут отображаться неправильно. Коррекция осуществляется выбором шрифта, правильно воспроизводящего кириллицу. Дайте команду Format > Equation (Формат > Выражение), в раскрывшемся списке Style Name (Имя стиля) выберите пункт Variables (Переменные) и щелкните на кнопке Modify (Изменить). Для задания шрифта используйте поле со списком Шрифт.

Задание 3. Построение трехмерных графиков

Задача. Изобразить на графике приблизительную форму электронных облаков в атоме.

Математическая постановка. При магнитном моменте электрона, равном нулю, форма электронного облака зависит только от квантового числа l (значения 0…3 соответствует s-, p-, d- и f-типам орбитали). Форма электронного облака определяется на основе многочленов Лежандра первого рода:

Параметрическое задание соответствующей поверхности имеет следующий вид:

Углы , φ изменяются в диапазоне от 0 до 2π.

Инструкция по выполнению.

1. Запустите MathCad.

2. Определите переменную L, которая укажет тип орбитали.

L:=3

3. Построение поверхности будем производить по точкам. Задайте два диапазона, которые будут определять изменение параметров , φ, задающих поверхность. Удобно определить границы диапазона в целых точках (через точку с запятой, на экране отображаются две точки), а затем произвести перемасштабирование на отрезок [0; 2π].

i:=0..100 j:=0..100

Для ввода индексов элементов (i) используйте соответствующую кнопку на панели инструментов Matrix (Матрица) (Отображение > панель инструментов > матрицы).

4. Определите двумерные матрицы, определяющие значения координат x, y, z в зависимости от значения параметров. Используйте названия переменных X0, Y0, Z0.

Для задания знака производной порядка l воспользуйтесь соответствующей кнопкой на панели инструментов Calculus (Вычисления)(Отображение > панель инструментов > мат.анализ).

5. Дайте команду Insert > Graph > Surface Plot (Вставка > График > Поверхность) или воспользуйтесь кнопкой Surface Plot (Поверхность) на панели инструментов Graph (График).

6. В появившейся области построения графика (рис. 3.2) вместо заполнителя укажите имена отображаемых матриц через запятую, заключив все их в скобки:

(X0,Y0,Z0)

7. Чтобы изменить формат построенного графика, дважды щелкните по его области. Откроется диалоговое 3-D Plot Format (Формат трехмерного графика).

8. На вкладке General (Общие) установите флажок Equal Scales (Равный масштаб), чтобы обеспечить одинаковый масштаб по осям координат.

9. На вкладке Appearance (Оформление) установите переключатель Fill Surface (Заливка поверхности), чтобы обеспечить заливку построенной поверхности.

10. На вкладке Lighting (Подсветка) включите режим освещения поверхности. Установите флажок Enable Lighting (Включить подсветку), отключите все источники света, кроме первого.

11. На панели Light Location (Размещение источника) задайте координаты источника света. Используйте кнопку Применить. По окончании настройки закройте диалоговое окно щелчком по кнопке OK.

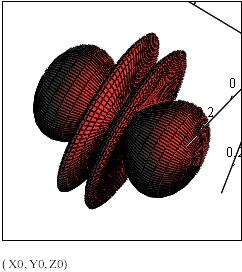
Рис. 3.2. Трехмерное изображение электронной f-орбитали (при l=3)

7. Протягиванием мыши в области графика измените направление осей координат, чтобы изображение было видно наиболее отчетливо.

8. Изменяя значение L, можно увидеть форму электронных облаков для разных орбиталей, в том числе и не встречающихся в природе.

9. Постройте трехмерные графики следующих функций, заданных в явной форме: z=x²+y²; z=xy.

• Мы научились строить трехмерные изображения объемных поверхностей, заданных параметрически и в явной форме. Фактически таким образом можно изобразить любые фигуры.

Задание 4. Решение дифференциальных уравнений

Задача. Найти функцию y(x), являющуюся решением дифференциального уравнения и имеющую значение 0 при x=0.

Математическая постановка. Это простое дифференциальное уравнение имеет точное аналитическое решение, однако в данном упражнении предполагается использование стандартной функции программы MathCad, осуществляющей численное (т.е. всегда приближенное) решение уравнения. Результат можно затем сравнить с точным решением.

Инструкция по выполнению.

1. Запустите MathCad.

2. Задайте начальное значение функции: y₀:=0. В общем случае формируется вектор начальных значений, количество элементов которого равно количеству решаемых уравнений (в данном случае уравнение одно).

3. Создайте функцию T(x,y), которая вычисляет значение производной при заданных значениях переменной и неизвестной функции:

T(x,y):=y₀+xcos(x)

4. Определите начальное (точка 0) и конечное значение отрезка интегрирования.

a:=0 b:=12π

5. Укажите число шагов интегрирования K:=20

6. Вычислите численное решение уравнения при помощи функции rkfixed.

Z:=rkfixed(y,a,b,K,T)

Результат вычисления – матрица Z с двумя столбцами, первый из которых содержит значения независимой переменной x, а второй – соответствующие значения функции y.

7. Определите аналитическое решение дифференциального уравнения:

y(x):=0.5xcos(x)+0.5xsin(x)0.5sin(x)

8. Постройте на одной координатной плоскости графики численного и точного решений так же, как в задаче 2. В нижней части области построения графика укажите в качестве независимых переменных (через запятую) Z^<0> и x. Сравните поведение численного и точного решений.

9. Измените число шагов, на которые делится отрезок интегрирования (дискретизацию расчетной области), и исследуйте, как изменится результат расчета при уменьшении и увеличении этого параметра.

• Мы научились численно решать дифференциальные уравнения первого порядка с помощью MathCad. Используемый метод полностью применим к системам, содержащим два или более дифференциальных уравнений.