5.3.Вычисление производных с помощью интерполяционных формул

Разностные формулы для производных не годятся в тех случаях, когда необходимо вычислить производную в произвольной точке, не совпадающей с узлами x_i. В этих случаях естественно воспользоваться интерполяционными формулами.

5.3.1.Равномерное распределение узлов

Пусть заданы значения функции y_i = f(x_i) в узлах x_i, равномерно распределенных на отрезке [a, b]:

x_i = a + ih, i = 0, 1, …, n; h = (b – a)/n.

Построим формулы приближенного дифференцирования с помощью первой интерполяционной формулы Ньютона (4.13), которую после некоторых упрощений можно записать в виде

(5.23)

где q = (x – x₀)/h. Мы здесь предполагаем, что узлы интерполяции распределены на отрезке [a, b] равномерно с шагом h.

Выберем в качестве x₀ узел, ближайший к точке x. Дифференцируя (5.23) по переменной x и учитывая, что

,

получим приближенные формулы для вычисления производных:

, (5.24)

. (5.25)

Чем больше слагаемых в формулах (5.24) и (5.25) используется, тем выше точность вычисления производных. Эти формулы дают хорошие приближения для точек, близких к значению x₀ (левому концу отрезка [a, b]).

Если x = x₀, то q = 0 и для вычисления производных в узлах x_i получим формулы

, (5.26)

. (5.27)

Очевидно, что вторая интерполяционная формула Ньютона позволяет вывести формулы для вычисления производных в точках, близких к правому краю x_n отрезка [a, b]:

(5.28)

(5.29)

(5.30)

При x = x_n получим

(5.31)

(5.32)

Пример 5.4. Вычислить приближенно первую и вторую производные функции cos2x в точках x = 0,55 и x = 0,96 по её значениям в точках 0,5; 0,6; 0,7; …1.

Решение. Построим таблицу разностей функции (Табл.5.7).

Табл. 5.7

i	xi	yi	Δyi	Δ2yi	Δ3yi	Δ4yi
0	0,5	0,540302	-0,17794	-0,01445	0,00767	0,00027
1	0,6	0,362358	-0,19239	-0,00678	0,00794	-4,6E-05
2	0,7	0,169967	-0,19917	0,001164	0,007894
3	0,8	-0,0292	-0,198	0,009058
4	0,9	-0,2272	-0,18894
5	1	-0,41615

Вычислим по формуле (5.24) приближенное значение производной первого порядка в точке x = 0,55:

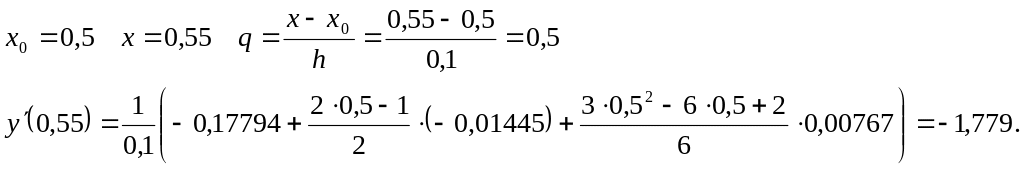
Мы здесь использовали только три слагаемых формулы (5.24). Значение производной по точной формуле равно

.

Относительная погрешность приближенного значения составляет

Найдем в точке x = 0,55 приближенное значение второй производной по формуле (5.25), ограничившись тремя слагаемыми:

Значение второй производной в точке x = 0,55 равно

Найдем относительную погрешность приближенного значения

Вычислим с помощью формулы (5.29) приближенное значение первой производной в точке x = 0,96:

Значение производной в точке x = 0,96 по точной формуле равно

.

Найдем относительную погрешность приближенного значения

Теперь найдем с помощью формулы (5.30) приближенное значение второй производной в точке x = 0,96:

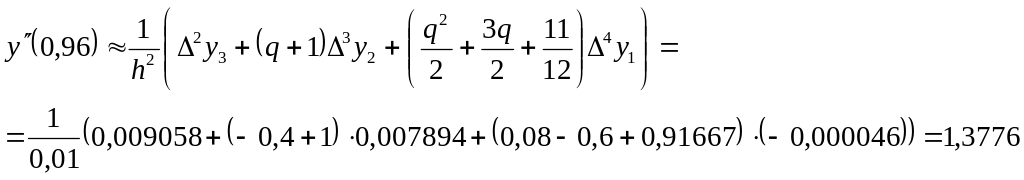
Значение второй производной в точке x = 0,96 равно

Относительная погрешность в данном случае равна

Как видим, формулы (5.24), (5.25) дают высокую точность при вычислении производной около левой границы отрезка, а формулы (5.29), (5.30) — около правой границы.

Выведем формулы для производной с помощью интерполяционного многочлена Лагранжа:

В случае равномерного распределения узлов с помощью обозначений

получим

Тогда полином Лагранжа запишется в виде

.

Найдем производную

. (5.33)

С помощью (5.33) получим формулы для вычисления производной в точках x_i при различных значениях n

1) n = 2. Используются три точки, и производная в этих точках выражается формулами

(5.34)

2) n = 3 (Четыре точки).

(5.35)

2) n = 4 (Пять точек).

(5.36)