5.Численное дифференцирование

Задача приближенного вычисления производной может возникнуть в тех случаях, когда неизвестно аналитическое выражение для исследуемой функции. Функция может быть задана таблично, или известен только график функции, полученный, например, в результате показаний датчиков параметров технологического процесса.

Иногда, при решении некоторых задач на компьютере, из-за громоздкости выкладок может оказаться более удобным вычисление производных численным методом, чем аналитическим. При этом, разумеется, необходимо обосновать применяемый численный метод, т.е. убедиться в том, что погрешность численного метода находится в приемлемых границах.

Одним из эффективных методов решения дифференциальных уравнений является разностный метод, когда вместо искомой функции рассматривается таблица её значений в определенных точках, при этом производные приближенно заменяются разностными формулами (см. ниже п.5.2 и главы 7, 8).

5.1.Графическое дифференцирование

Пусть известен график функции y = f(x) на отрезке [a, b]. Можно построить график производной функции, вспомнив ее геометрический смысл. Воспользуемся тем фактом, что производная функции в точке x равна тангенсу угла наклона к оси абсцисс касательной к её графику в этой точке.

Если x = x₀, то найдем y₀ = f(x₀) с помощью графика и затем проведем касательную AB к графику функции в точке (x₀, y₀) (рис. 5.1). Проведем прямую, параллельную касательной AB, через точку (–1, 0) и найдем точку y₁ её пересечения с осью ординат. Тогда значение y₁ равно тангенсу угла наклона касательной к оси абсцисс, т.е. производной функции f(x) в точке x₀:

,

и точка M₀(x₀, y₁) принадлежит графику производной.

Рис. 5.1.

Чтобы построить график производной необходимо разбить отрезок [a, b] на несколько частей точками x_i, затем для каждой точки графически построить значение производной и соединить полученные точки плавной кривой с помощью лекал.

На рис. 5.2 показано построение пяти точек M₁, M₂, …, M₅ и графика производной.

Алгоритм построения графика производной:

1. Строим касательную к графику функции y = f(x) в точке (x₁, f(x₁));

из точки (–1, 0) параллельно касательной в точке (x₁, f(x₁)) проведем прямую до пересечения с осью ординат; эта точка пересечения дает значение производной . Строим точку .

2. Аналогично построим остальные точки M₂, M₃, M₄ и M₅.

3. Соединяем точки M₁, M₂, M₃, M₄, M₅ плавной кривой.

Полученная кривая является графиком производной.

Рис. 5.2.

Точность графического способа определения производной невысока. Мы приводим описание этого способа только в учебных целях.

Замечание. Если в алгоритме построения графика производной вместо точки (–1, 0) взять точку (–l, 0), где l > 0, то график будет построен в другом масштабе по оси ординат.

5.2.Разностные формулы

5.2.1.Разностные формулы для обыкновенных производных

Разностные формулы для приближенного вычисления производной подсказаны самим определением производной.

Пусть значения функции в точках x_i обозначены через y_i:

y_i = f(x_i), x_i = a + ih, i = 0, 1, …, n; h = (b – a)/n.

Мы рассматриваем случай равномерного распределения точек на отрезке [a, b]. Для приближенного вычисления производных в точках x_i можно использовать следующие разностные формулы, или разностные производные.

. (5.1)

. (5.2)

. (5.3)

Так как предел отношения (5.1) при h → 0 равен правой производной в точке x_i, то это отношение иногда называют правой разностной производной в точке x_i. По аналогичной причине отношение (5.2) называют левой разностной производной в точке x_i. Отношение (5.3) называют центральной разностной производной в точке x_i.

Оценим погрешность разностных формул (5.1) — (5.3), предполагая, что функция f(x) разлагается в ряд Тейлора в окрестности точки x_i:

(5.4)

Полагая в (5.4) x = x_i + h или x = x_i – h, получим

(5.5)

(5.6)

Учитывая (5.5) и (5.6) имеем

. (5.7)

. (5.8)

. (5.9)

Из последних соотношений следует, что разностная формула (5.3) имеет погрешность на порядок меньшую, чем разностные формулы (5.1) и (5.2).

Пример 5.1. Вычислить приближенно производные с помощью разностных формул и сравнить с точными значениями производной функции y = sin x в точках отрезка [0, 1].

Решение в Excel. Составим таблицу значений функции y = sin πx на отрезке [0, 1] с шагом 0,1 (табл. 5.1).

В ячейку B2 введем формулу =SIN(A2*3,1415926) и протянем ячейку B2 маркером заполнения до ячейки B12.

В ячейки C3, D3, E3 и F3 введем соответственно формулы =(B4-B3)/(A4-A3), =(B3-B2)/(A3-A2), =(B4-B2)/(A4-A2) и =3,1415926*COS(A3*3,1415926), выделим диапазон C3:F3 и протянем маркером заполнения до строки 11.

Табл. 5.1

	A	B	C	D	E	F
1	xi	yi = sin xi	Разностная формула (5.1)	Разностная формула (5.2)	Разностная формула (5.3)	Производная cos xi
2	0	0
3	0,1	0,309017	2,787683	3,09017	2,938926	2,987832
4	0,2	0,587785	2,212317	2,787683	2,5	2,541602
5	0,3	0,809017	1,420395	2,212317	1,816356	1,846582
6	0,4	0,951057	0,489435	1,420395	0,954915	0,970806
7	0,5	1	-0,48943	0,489435	8,28E-08	8,42E-08
8	0,6	0,951057	-1,4204	-0,48943	-0,95491	-0,97081
9	0,7	0,809017	-2,21232	-1,4204	-1,81636	-1,84658
10	0,8	0,587785	-2,78768	-2,21232	-2,5	-2,5416
11	0,9	0,309017	-3,09017	-2,78768	-2,93893	-2,98783
12	1	5,36E-08

Результат представлен также графиком на рис. 5.3. Как видно на рисунке, разностная формула (5.3) дает практически те же значения, что и формула точной производной.

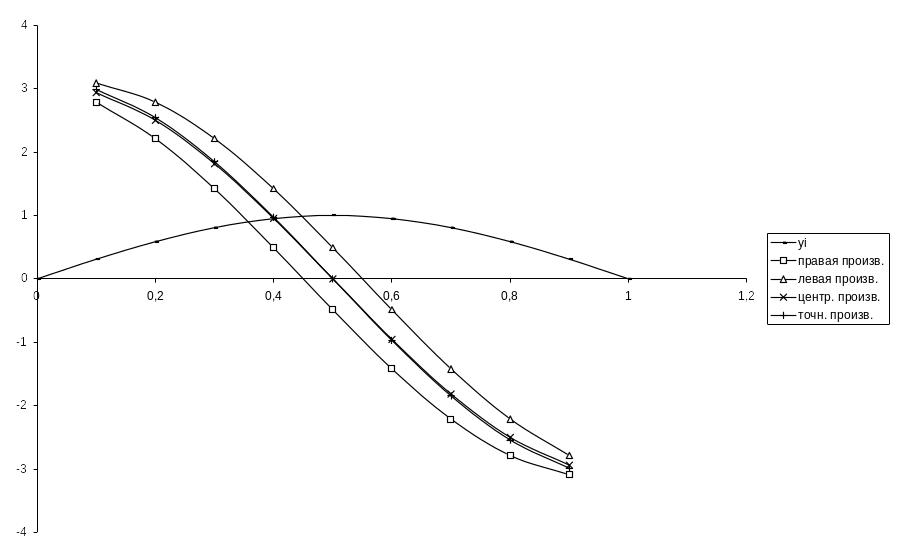
Рис. 5.3.

Производные высших порядков можно приближенно вычислять по формулам, полученным с помощью последовательного применения разностных соотношений (5.1) — (5.3).

Разностная формула для второй производной (разностная производная второго порядка) имеет вид:

. (5.10)

Непосредственной подстановкой разложений (5.5) и (5.6) в формулу (5.10) можно получить зависимость между второй производной функции и разностной формулой для производной второго порядка:

. (5.11)

Пример 5.2. Вычислить приближенно производную второго порядка и сравнить с точными значениями второй производной функции y = sin πx в точках отрезка [0, 1].

Решение в Excel. Составим таблицу значений функции y = sin πx на отрезке [0, 1] с шагом 0,2 (табл. 5.2), вычислим разностную производную второго порядка, производную второго порядка и относительную погрешность.

Вычислим те же величины с шагом 0,1 (табл.5.3).

Табл.5.2

xi	yi	Разностная формула (5.10)		Относительная погрешность
0	0
0,2	0,587785	-5,61285	-5,80121	0,032469
0,4	0,951057	-9,08178	-9,38655	0,032469
0,6	0,951057	-9,08178	-9,38655	0,032469
0,8	0,587785	-5,61285	-5,80121	0,032469
1	5,36E-08

Табл.5.3

xi	yi	Разностная формула (5.10)		Относительная погрешность
0	0
0,1	0,309017	-3,02487	-3,04988	0,008198
0,2	0,587785	-5,75365	-5,80121	0,008198
0,3	0,809017	-7,91922	-7,98468	0,008198
0,4	0,951057	-9,3096	-9,38655	0,008198
0,5	1	-9,7887	-9,8696	0,008198
0,6	0,951057	-9,3096	-9,38655	0,008198
0,7	0,809017	-7,91922	-7,98468	0,008198
0,8	0,587785	-5,75365	-5,80121	0,008198
0,9	0,309017	-3,02487	-3,04988	0,008198
1	5,36E-08

Уменьшение шага таблицы в два раза привело к уменьшению относительной ошибки в четыре раза! Это объясняется формулой погрешности (5.11).