4.5. О решении нелинейных систем методами спуска

Общий недостаток всех рассмотренных выше методов решения систем нелинейных уравнений — это сугубо локальный характер сходимости, затрудняющий их применение в случаях (довольно типичных), когда имеются проблемы с выбором хороших начальных приближений. Помощь здесь может прийти со стороны численных методов оптимизации — ветви вычислительной математики, обычно выделяемой в самостоятельную дисциплину. Для этого нужно поставить задачу нахождения решений данной нелинейной системы как оптимизационную или, иначе, экстремальную задачу. Ради геометрической интерпретации проводимых ниже рассуждений и их результатов ограничимся рассмотрением системы, состоящей из двух уравнений с двумя неизвестными (4.3.1).

Из функций f u g системы (4.3.1) образуем новую функцию

. (4.5.1)

Так как эта функция неотрицательна, то найдется точка (х*, у*) такая, что

,

т.е. (х*, у*)= argminФ(x, у). Следовательно, если тем или иным

способом удается получить точку (х*, у*), минимизирующую функцию Ф(х,у), и если при этом окажется, что min Ф(х,y) = Ф(х*, у*)=0, то (х*, у*) - искомое решение системы (4.3.1), поскольку

Последовательность точек ( ) — приближений к точке (х*; у*) минимума Ф(х, у) — обычно получают по рекуррентной формуле

, k =0,1,2,..., (4.5.2)

где — вектор, определяющий направление минимизации, а а_к - скалярная величина, характеризующая величину шага минимизации (шаговый множитель). Учитывая геометрический смысл задачи минимизации функции двух переменных Ф(х,.у) — «спуск на дно» поверхности z=Ф(x,y) (см. рис.1), итерационный метод (4.5.2) можно назвать методом спуска, если вектор при каждом k является направлением спуска (т.е. существует такое, что и если множитель а_к подбирается так, чтобы выполнялось условие релаксации , означающее переход на каждой итерации в точку с меньшим значением минимизируемой функции.

Итак, при построении численного метода вида (4.5.2) минимизации функции Ф(х, у) следует ответить на два главных вопроса: как выбирать направление спуска и как регулировать длину шага в выбранном направлении с помощью скалярного параметра — шагового множителя а_к. Приведем наиболее простые соображения по этому поводу.

При выборе направления спуска естественным является выбор такого направления, в котором минимизируемая функция убывает наиболее быстро. Как известно из математического анализа функций нескольких переменных, направление наибольшего возрастания функции в данной точке показывает ее градиент в этой точке. Поэтому примем за направление спуска вектор

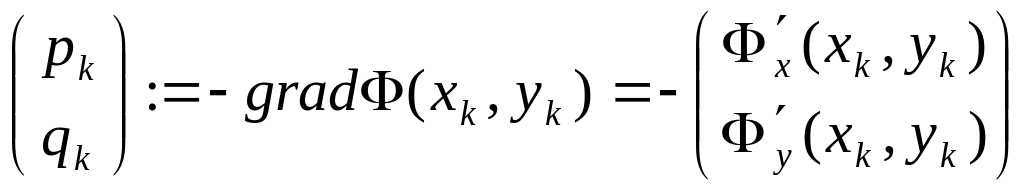
— антиградиент функции Ф(х, у). Таким образом, из семейства методов (4.5.2) выделяем градиентный метод

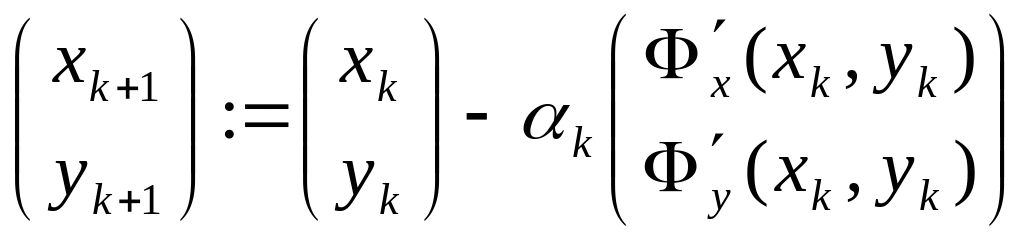. (4.5.3)

Оптимальный шаг в направлении антиградиента —- это такой шаг, при котором значение — наименьшее среди всех других значений Ф(х,у) в этом фиксированном направлении, т.е. когда точка ( ) является точкой условного минимума. Следовательно, можно рассчитывать на наиболее быструю сходимость метода (4.5.3), если полагать в нем такой выбор шагового множителя, называемый исчерпывающим спуском, вместе с формулой (4.5.3) определяет метод наискорейшего спуска.

Геометрическая интерпретация этого метода хорошо видна из рис. 1, 2. Характерны девяностоградусные изломы траектории наискорейшего спуска, что объясняется исчерпываемостью спуска и свойством градиента (а значит, и антиградиента) быть перпендикулярным к касательной к линии уровня в соответствующей точке

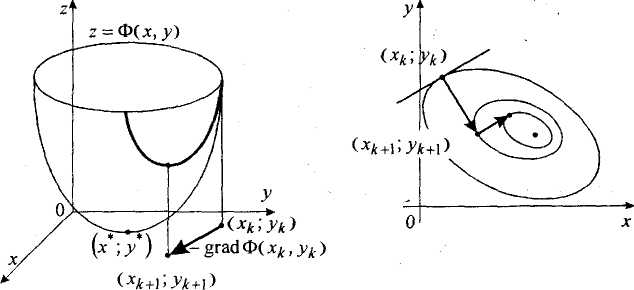
Рис. 1. Пространственная интер- Рис. 2. Траектория наискорей-претация метода наискорейшего шего спуска для функции (4.5.1) спуска для функции (4.5.1)

Наиболее типичной является ситуация, когда найти точно (аналитическими методами) оптимальное значение а_к не удается. Следовательно, приходится делать ставку на применение каких-либо численных методов одномерной минимизации и находить а_к лишь приближенно.

Несмотря на то, что задача нахождения минимума функции одной переменной намного проще, чем решаемая задача, применение тех или иных численных методов нахождения значений той или иной точностью требует вычисления нескольких значений минимизируемой функции. Так как это нужно делать на каждом итерационном шаге, то при большом числе шагов реализация метода наискорейшего спуска в чистом виде является достаточно высокозатратной. Существуют эффективные схемы приближенного вычисления квазиоптимальных а_к, в которых учитывается специфика минимизируемых функций (типа сумм квадратов функций).

Зачастую успешной является такая стратегия градиентного метода, при которой шаговый множитель а_к в (4.5.3) берется либо сразу достаточно малым постоянным, либо предусматривается его уменьшение, например, делением пополам для удовлетворения условию релаксации на очередном шаге. Хотя каждый отдельный шаг градиентного метода при этом, вообще говоря, далек от оптимального, такой процесс по количеству вычислений функции может оказаться более эффективным, чем метод наискорейшего спуска.

Главное достоинство градиентных методов решения нелинейных систем — глобальная сходимость. Нетрудно доказать, что процесс градиентного спуска приведет к какой-либо точке минимума функции из любой начальной точки. При определенных условиях найденная точка минимума будет искомым решением исходной нелинейной системы.

Главный недостаток — медленная сходимость. Доказано, что сходимость таких методов — лишь линейная, причем, если для многих методов, таких как метод Ньютона, характерно ускорение сходимости при приближении к решению, то здесь имеет место скорее обратное. Поэтому есть резон в построении гибридных алгоритмов, которые начинали бы поиск искомой точки — решения данной нелинейной системы — глобально сходящимся градиентным методом, а затем производили уточнение каким-то быстросходящимся методом, например, методом Ньютона (разумеется, если данные функции обладают нужными свойствами).

Разработан ряд методов решения экстремальных задач, которые соединяют в себе низкую требовательность к выбору начальной точки и высокую скорость сходимости. К таким методам, называемым квазиньютоновскими, можно отнести, например, метод переменной метрики (Дэвидона-Флетчера-Пауэлла), симметричный и положительно определенный методы секущих.

При наличии негладких функций в решаемой задаче следует отказаться от использования производных или их аппроксимаций и прибегнуть к так называемым методам прямого поиска (циклического покоординатного спуска, Хука иДживса, Розенброка и т.п.).

Практическая часть

1. Вычисление погрешностей

Задание

Пусть a, b, y – приближенные числа с верными в строгом смысле значащими цифрами, х – верное число. Вычислите:

Оцените погрешность результата. Результаты расчетов расположите в таблице.

Решение

Представлено на рисунке 1.1.

a	2,41	b	-0,794	x	2,019	y	1,96
∆a	0,005	∆b	0,0005	∆x	0,0005	∆y	0,005
δa	0,207469	δb	0,062972	δx	0,024765	δy	0,255102
z1	-1,91	z2	7,53	z3	-9,44	z4	0,925	z	-10,2031
∆z1	0,005175	∆z2	0,003765	∆z3	0,00141	∆z4	-0,00022	∆z	0,003914
δz1	0,270441	δz2	0,05	δz3	0,014835	δz4	-0,02342	δz	-0,00858
-1,91354	a*b
7,53079	exp(x)
-9,44	z1-z2
0,925212	sin(y)

Рисунок 1.1 – Результаты расчетов.

Численное решение алгебраических уравнений

Задание 1

Отделите графически один из корней уравнения и определите его с точностью до E=0,05*10^-4 методом простой итерации.

Решение

Исходные данные:

Определим графически один из корней. Значения переменных указаны в таблице 1.1. Графическое решение представлено на рисунке 1.2.

Таблица 1.1 – Значение переменных

X	Y
-5	-46
-4	-5
-3	6
-2	-1
-1	-14
0	-21
1	-10
2	31
3	114
4	251
5	454

Рисунок 1.2 – Графическое решение

На графике видно, что имеется 3 корня уравнения, которые находятся на отрезках [-5; -3], [-3; -1], [1; 2].

Задание 2.

Отделите один из корней уравнения и определите его с точностью до E=0,05*10^-4 методом касательных, комбинированным методом хорд и касательных.

Программная реализация методов на языке С++ представлена в листинге 1.1.

Листинг 1.1 – Методы касательных и комбинированный хорд и касательных.

#include<iostream.h>

#include<stdlib.h>

#include<math.h>

#include<conio.h>

void main()

{int n;

float x, y, x1,y1,t,E;

clrscr();

n=1; E=0.00005;

cout<<"Vvedite nachalo otrezka\n x = ";

cin>>x;

cout<<"Vvedite konetc otrezka\n y = ";

cin>>y;

do

{n++;

y1 = y - (pow(2*y,3) + pow(9*y,2) - 21)/(3*pow(2*y,2) + 2*pow(y,1) - 21);

x1=x-((y-x)/((pow(2*y,3)+pow(9*y,2)-21)-(pow(2*x,3)+pow(9*x,2)-21)))*(pow(2*x,3)+pow(9*x,2)-21);

x = x1;

y = y1;

}

while ((x-y)>=2*E);

t=(x+y)/2;

cout<<"Koren = "<<t<<endl;

cout<<"kol-vo iteratciy n = "<<n<<endl;

getch();

}

Результат работы программы: