4.3. Метод брауна

В отличие от пошаговой линеаризации векторной функции F(x), приведшей к методу Ньютона (3.1.2), Брауном (1966 г.) предложено проводить на каждом итерационном шаге поочередную линеаризацию компонент вектор-функции F(x), т.е. линеаризовать в системе (2.1) сначала функцию , затем и т.д., и последовательно решать получаемые таким образом уравнения. Чтобы не затенять эту идею громоздкими выкладками и лишними индексами, рассмотрим вывод расчетных формул метода Брауна в двумерном случае.

Пусть требуется найти решение системы

(4.3.1)

и пусть уже получены приближения .

Подменим первое уравнение системы (4.3.1) линейным, полученным по формуле Тейлора для функции двух переменных:

Отсюда выражаем х (обозначим этот результат через ):

(4.3.2)

При находим значение переменной :

которое будем считать лишь промежуточным приближением (т.е. не ), поскольку оно не учитывает второго уравнения системы (4.3.1).

Подставив в g(x, у) вместо х переменную , придем к некоторой функции G(y) := g( , у) только одной переменной у. Это позволяет линеаризовать второе уравнение системы (4.3.1) с помощью формулы Тейлора для функции одной переменной:

(4.3.3)

При нахождении производной G'(y) нужно учесть, что G(y) = g( (y), у) есть сложная функция одной переменной у, т.е. применить формулу полной производной

Дифференцируя по у равенство (4.3.2), получаем выражение

подстановка которого в предыдущее равенство при дает

При известных значениях G( ) = g( k, ) и G'( ) теперь можно разрешить линейное уравнение (4.3.3) относительно у (назовем полученное значение ):

Заменяя в (4.3.2) переменную у найденным значением , приходим к значению

Таким образом, реализация метода Брауна решения двумерных нелинейных систем вида (4.3.1) сводится к следующему.

При выбранных начальных значениях каждое последующее приближение по методу Брауна находится при k = 0,1,2,... с помощью совокупности формул

,

счет по которым должен выполнятся в той очередности, в которой они записаны.

Вычисления в методе Брауна естественно заканчивать, когда выполнится неравенство (с результатом ). В ходе вычислений следует контролировать немалость знаменателей расчетных формул. Заметим, что функции f и g в этом методе неравноправны, и перемена их ролями может изменить, ситуацию со сходимостью.

Указывая на наличие квадратичной сходимости метода Брауна, отмечают, что рассчитывать на его большую по сравнению с методом Ньютона эффективность в смысле вычислительных затрат можно лишь в случае, когда фигурирующие в нем частные производные заменяются разностными отношениями.

4.4. Метод секущих бройдена

Чтобы приблизиться к пониманию идей, лежащих в основе предлагаемого вниманию метода, вернемся сначала к изучавше­муся в двух предыдущих главах одномерному случаю.

В процессе построения методов Ньютона и секущих решения нелинейного скалярного уравнения

(4.4.1)

ф ункция f(x) в окрестности текущей точки подменяется линейной функцией (аффинной моделью)

(4.4.1а)

Приравнивание к нулю последней, т.е. решение линейного уравнения

,

порождает итерационную формулу

(4.4.2)

для вычисления приближений к корню уравнения (4.4.1).

Если потребовать, чтобы заменяющая функцию f(x) вблизи точки аффинная модель имела в этой точке одинаковую с ней производную, то, дифференцируя (4.4.1а), получаем Значение коэффициента

,

подстановка которого в (4.4.2) приводит к известному методу Ньютона (5.14). Если же исходить из того, что наряду с равенством должно иметь место совпадение функций f(x) и в предшествующей точке т.е. из равенства

,

или, в соответствии с (4.4.1а)

, (4.4.3)

то получаем коэффициент

,

превращающий (4.4.2) в известную формулу секущих.

Равенство (4.4.3), переписанное в виде

,

называют соотношением секущих в Оно легко обобщается на n -мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.

В n-мерном векторном пространстве соотношение секущих представляется равенством

, (4.4.4)

где — известные n-мерные векторы, — данное нелинейное отображение, а — некоторая матрица линейного преобразования в . С обозначениями

, (4.4.5)

соотношение секущих в обретает более короткую запись:

(4.4.4а)

Аналогично одномерному случаю, а именно, по аналогии с формулой (4.4.2), будем искать приближения к решению векторного уравнения (2.1а) по формуле

(4.4.6)

Желая, чтобы эта формула обобщала метод секущих (5.32), обратимую n x n-матрицу в ней нужно подобрать так, чтобы она удовлетворяла соотношению секущих (4.4.4). Но это соотношение не определяет однозначно матрицу : глядя на равенство (4.4.4а), легко понять, что при n>1 существует множество матриц , преобразующих заданный n-мерный вектор в другой заданный вектор (отсюда — ясность в понимании того, что могут быть различные обобщения одномерного метода секущих).

При формировании матрицы будем рассуждать следующим образом.

Переходя от имеющейся в точке аффинной модели функции F(x)

(4.4.7)

к такой же модели в точке

(4.4.8)

мы не имеем о матрице линейного преобразования никаких сведений, кроме соотношения секущих (4.4.4). Поэтому исходим из того, что при этом переходе изменения в модели должны быть минимальными. Эти изменения характеризует разность . Вычтем из равенства (4.4.8) определяющее равенство (4.4.7) и преобразуем результат, привлекая соотношение секущих (4.4.4). Имеем:

Представим вектор в виде линейной комбинации фиксированного вектора определенного в (4.4.5), и некоторого вектора t, ему ортогонального:

,

Подстановкой этого представления вектора в разность получаем другой ее вид

(4.4.9)

Анализируя выражение (4.4.9), замечаем, что первое слагаемое в нем не может быть изменено, поскольку

- фиксированный вектор при фиксированном k. Поэтому минимальному изменению аффинной модели будет отвечать случай, когда второе слагаемое в (4.4.9) будет нуль-вектором при Iвсяких векторах t, ортогональных векторам , т.е. следует находить из условия

. (4.4.10)

Непосредственной проверкой убеждаемся, что условие (4.4.10) будет выполнено, если матричную поправку взять в виде одноранговой nхn-матрицы

.

Таким образом, приходим к так называемой формуле пересчета С. Бройдена (1965 г.)

(4.4.11)

которая позволяет простыми вычислениями перейти от старой матрицы к новой такой, чтобы выполнялось соотношение секущих (4.4.4а) в новой точке и при этом изменения в аффинной модели (4.4.7) были минимальны

Совокупность формул (4.4.6), (4.4.11) вместе с обозначениями (4.4.5) называют методом секущих Бройдена или просто методом Бройдена решения систем нелинейных числовых уравнений.

Хотя в методах секущих обычным является задание двух начальных векторов ( и ), для метода Бройдена характерно другое начало итерационного процесса. Здесь нужно задать один начальный вектор , начальную матрицу и далее в цикле по k = 0,1,2,... последовательно выполнять следующие операции:

1. решить линейную систему

(4.4.12)

относительно вектора :

2. найти векторы и :

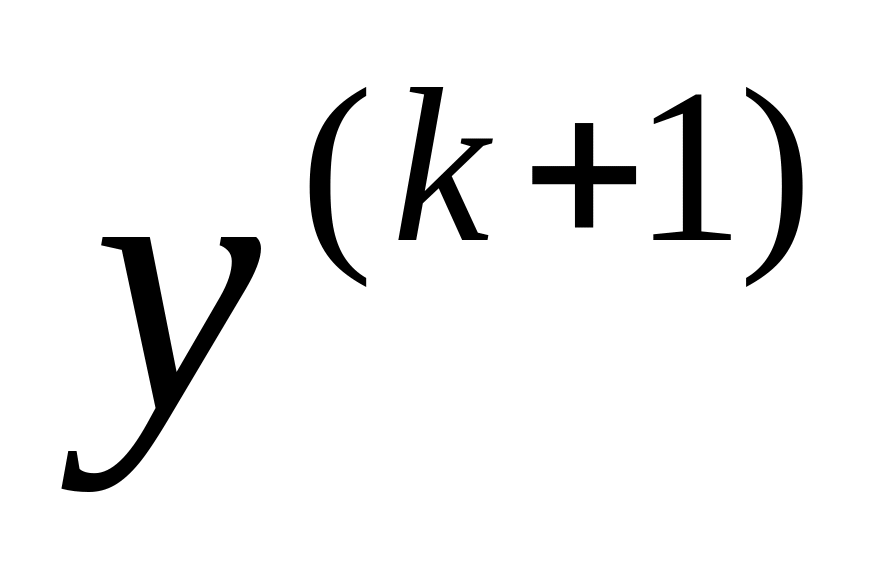, ; (4.4.13)

3. сделать проверку на останов (например, с помощью проверки на малость величин 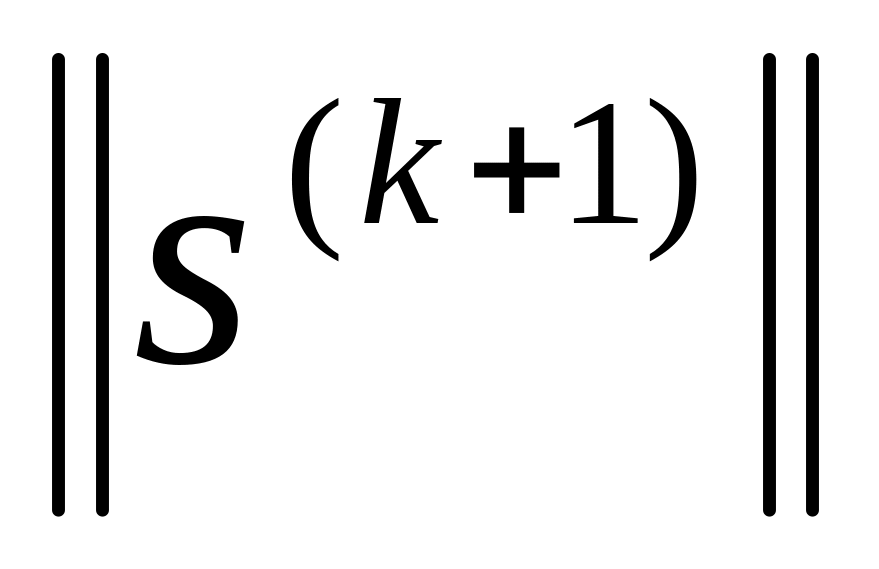и/или 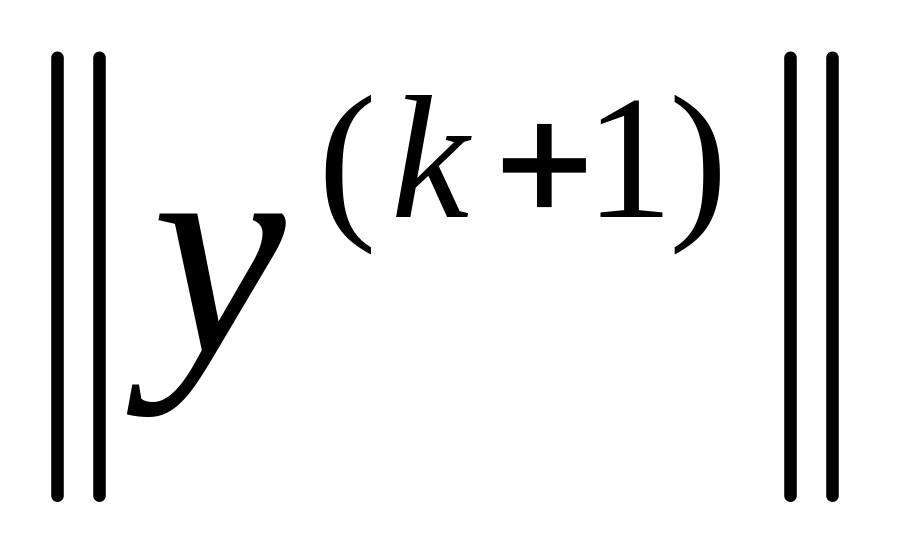и если нужная точность не достигнута, вычислить новую матрицу по формуле пересчета (см. (4.4.11))

(4.4.14)

В качестве матрицы , требуемой равенством (4.4.12) для запуска итерационного процесса Бройдена, чаще всего берут матрицу Якоби или какую-нибудь ее аппроксимацию. При этом получаемые далее пересчетом (4.4.14) матрицы , ,... не всегда можно считать близкими к соответствующим матрицам Якоби , ,... (что может иногда сыграть полезную роль при вырождении матриц ). Но, в то же время, показывается, что при определенных требованиях к матрицам Якоби матрицы обладают «свойством ограниченного ухудшения», означающим, что если и происходит увеличение с увеличением номера итерации k, то достаточно медленно. С помощью этого свойства доказываются утверждения о линейной сходимости ( ) к х*

при достаточной близости к х* и к а в тех предположениях, при которых можно доказать квадратичную сходимость метода Ньютона (3.1.2), — о сверхлинейной сходимости последовательности приближений по методу Бройдена.

Как и в случаях применения других методов решения нелинейных систем, проверка выполнимости каких-то условий сходимости итерационного процесса Бройдена весьма затруднительна.

Формуле пересчета (4.4.14) в итерационном процессе можно придать чуть более простой вид.

Так как, в силу (4.4.12) и (4.4.13),

,

а

,

то из формулы (4.4.14) получаем формально эквивалентную ей формулу пересчета

, (4.4.14а)

которую можно использовать вместо (4.4.14) в совокупности с формулой (4.4.6) или с (4.4.12), (4.4.13) (без вычисления вектора ). Такое преобразование итерационного процесса Бройдена несколько сокращает объем вычислений (на одно матрично-векторное умножение на каждой итерации). Не следует, правда, забывать, что при замене формулы (4.4.14) формулой (4.4.14а) может измениться ситуация с вычислительной устойчивостью метода; к счастью, это случается здесь крайне редко, а именно, в тех случаях, когда для получения решения с нужной точностью требуется много итераций по методу Бройдена, т.е. когда и применять его не стоит.