Глава 6. 18-ьм-модель

Алгебраический вид функции совокупного спроса выво­дится путем подстановки значения ставки процента, опре­деленного из уравнения кривой ЬМ,ъ уравнение линии 18.

Полный дифференциал функции совокупного спроса представляет собой модель взаимодействия рынков благ и денег в кейнсианской модели.

Глава 7 рынок труда

На рынке труда в результате взаимодействия спроса на труд с его предложением определяется уровень занятости, а следовательно, и объем предложения благ в коротком пе­риоде, так как при заданном объеме капитала и существую­щей технологии объем производства благ становится функ­цией одной переменной: у = у^}.

На рынке труда мы встречаемся с таким социально-эко­номическим феноменом, как безработица, под которой по­нимается превышение предложения труда над спросом на

труд.

Неоклассики и кейнсианцы неодинаково интерпрети­руют процесс функционирования рынка труда и приходят к различным выводам относительно причин, порождающих безработицу.

7.1. Равновесие на рынке труда и безработица 7.1.1. Спрос на труд

Неоклассическая функция спроса на труд. Основыва­ется на предположении, что и на рынке благ, и на рынке факторов производства господствует совершенная конку­ренция. В этом случае, как обосновывается в микроэко­номике, предприниматели получают максимум прибыли, если ценность предельного продукта труда равняется но­минальной ставке заработной платы:

ЛN

(7.1)

192

Глава 7. Рынок труда

7.1. Равновесие на рынке труда и безработица

193

Левая часть уравнения (7.1) показывает, на сколько возрастет выручка фирмы при увеличении использования труда на единицу, а правая — на сколько при этом воз­растут затраты фирмы на оплату труда. До тех пор пока Р(^у/(1N > \У, увеличение занятости сопровождается ростом прибыли. Если обе части уравнения (7.1) разделить на Р, то условие максимизации прибыли примет вид

Ау V/

_ »_ — __ — 111

АN " Р '

где и> - ставка реальной зарплаты.

При снижении ставки реальной зарплаты для получе­ния максимума прибыли потребуется использовать больше труда, и наоборот. Следовательно, спрос предпринимателей на труд представляется функцией № = №(ю).

В случаях, когда технология отображается производ­ственной функцией Кобба — Дугласа: у = №¹К¹~^а, явный вид неоклассической функции спроса на труд выводится из решения следующей задачи:

тах,

- гК₀ -

где тг - - прибыль; К₀ — фиксированный объем капитала. Прибыль достигает максимума при

N^{^} =

Отсюда следует, что

ш

_а\1(а-\)

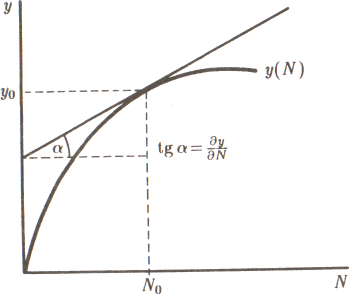
Графически определение объема спроса на труд в нео­классической концепции представлено на рис. 7.1. В верх­ней части изображен график производственной функции у = г/^). Тангенс угла наклона касательной к этому гра­фику представляет предельную производительность труда при соответствующем числе занятых.

На основе изменения величины 1;§а по мере движения вдоль кривой у(N) в нижней части рис. 7.1 строится гра­фик предельной производительности труда. (Примет ли он

вид прямой линии, выпуклой кривой или вогнутой кри­вой — зависит от скорости изменения крутизны графика производственной функции).

.

эл/¹

Чтобы определить объем спроса на труд, нужно на график пре­дельной производи­тельности труда нало­жить график ставки ре­альной заработной пла­ты (ад). Точка их пере­сечения укажет на ко­личество труда (Л^о)» обеспечивающее мак­симум прибыли. Зная количество используе­мого труда, по графику производственной фун­кции можно опреде­лить объем выпус­ка (уо).

Рис. 7.1. Графическое построение нео­классической функции спроса на труд.

/V»

/V,

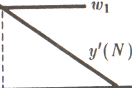
N

•И>0

В коротком пери­оде спрос на труд меня­ется только в резуль­тате изменения ставки реальной заработной платы: при ее сниже­нии занятость растет, при ее повышении за­нятость уменьшается (рис. 7.1).

В длительном периоде количество используемого труда может измениться вследствие технического прогресса или увеличения объема применяемого капитала. В том и другом случае график производственной функции сдви­нется вверх, как это показано в верхней части рис. 7.2. Соответственно вверх сдвигается и график предельной производительности труда в нижней части данного ри­сунка.

194