Глава 5. Рынок капитала

5.3. Оптимизация структуры портфеля ценных бумаг

147

vi

12

Рис. 5.9. Доходность и риск портфелей в зависи­мости от коэффициента корреляции.

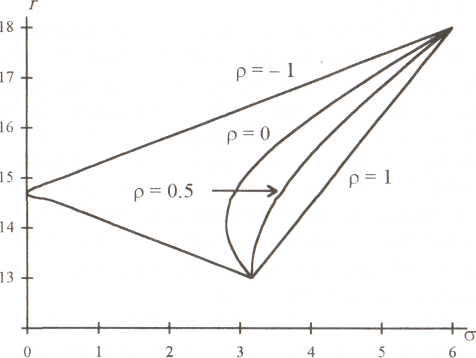
тора характеристик различных вариантов портфеля при 4 значениях р. На рис. 5.9 они представлены в графическом виде.

На какой точке кривых выбора остановится инвестор, зависит от его отношения к риску. Предпочтения инди­вида относительно дохода и риска можно представить в виде функции полезности: V = 1}(г,а). В зависимости от отношения к риску люди делятся на:

1. равнодушных к риску, считающих, что их благопо­ лучие остается неизменным, если в равной мере растут до­ ходность и степень риска портфеля;

2. предрасположенных к риску, которые согласны на отставание роста доходности от роста степени риска;

3. не расположенных к риску, для которых с повыше­ нием степени риска портфеля полезность его не меняется только в том случае, если доходность портфеля возрастет в большей мере, чем степень риска. Иначе говоря, чтобы по­ лезность портфеля не менялась, для первой категории лю­ дей производная доходности по риску должна быть посто­ янной; для второй — уменьшаться; для третьей — возра­ стать.

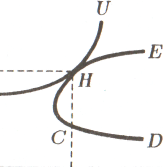
Рис. 5.10. Функция полез­ности инвестора.

Рис. 5.11. Оптимальный портфель.

Большинство людей относится к третьей группе. Они готовы платить за предотвращение или снижение риска. На этом основана деятельность страховых компаний, ус­пешно функционирующих в большинстве стран. Функ­цию полезности не расположенных к риску людей можно представить функцией, предложенной М. Рубинштейном:² V - фг_р - а-р, где ф - - коэффициент, характеризующий ин­дивидуальные предпочтения инвестора относительно доход­ности и риска. Графически такая функция изображается в виде семейства кривых безразличия инвестора (рис. 5.10), построенных по формуле г_р = (и + а*)/ф, где V - - заданная величина полезности.

Выпуклость кривых безразличия к оси абсцисс свиде­тельствует о том, что благосостояние инвестора не изме­нится лишь в том случае, если каждая дополнительная единица риска будет оплачиваться все возрастающей до­ходностью портфеля. Угол наклона касательной к кривой безразличия выражает размер требуемой инвестором платы за увеличение риска на единицу. Совместив карту безраз­личия инвестора с эффективной областью выбора (кривой 1)СЕ на рис. 5.8), получим геометрическое решение за­дачи оптимизации портфеля из двух разновидностей рис­ковых активов. Для не расположенных к риску людей от­резок СП на рис. 5.11 представляет нерациональные ком­бинации, так как каждой из них на отрезке СЕ соответ-

пзК ргетштв //

²ПиЫп81е1п М. Е. А сотрагаНуе з^ЬаИсз апа1уз1з Л. Визт. 1973. Уо1. 46. Р. 605.

148

Глава 5. Рынок капитала

5.3. Оптимизация структуры портфеля ценных бумаг

149

ствует комбинация, обеспечивающая большую доходность портфеля при той же степени риска.

Точка касания эффективной области выбора с наиболее удаленной кривой безразличия (точка Н на рис. 5.11) ука­жет на оптимальную комбинацию г*, а*, однозначно соот­ветствующую определенной доле га# (рис. 5.8), т. е. опти­мальной структуре портфеля.

Проведенный анализ оптимизации структуры порт­феля, состоящего из двух разновидностей акций, позволяет сделать следующие выводы.

1. Решение о приобретении рисковой ценной бумаги не­ льзя принимать йа основе изолированной оценки ее харак­ теристик.

2. Размер снижения риска портфеля за счет его дивер­ сификации определяется уровнем корреляции между от­ дельными ценными бумагами; чем ниже коэффициент кор­ реляции, тем больше возможности снижения риска.

3. Из двух рисковых ценных бумаг можно составить безрисковый портфель, если р - -1 или р - 1; в послед­ нем случае для этого необходимо осуществлять «пустые» продажи наиболее доходной ценной бумаги.

4. Определение оптимальной структуры портфеля пред­ полагает знание функции полезности инвестора, выражаю­ щей его отношение к различным сочетаниям доходности и риска.

5.3,2. Составление портфеля из п разновидностей ценных бумаг

Для определения области выбора инвестора при соста­влении портфеля из любого числа разновидностей риско­вых активов поступим следующим образом. Оптимальный портфель, составленный из двух пакетов акций А и В, бу­дем рассматривать в качестве одной из разновидностей цен­ных бумаг А В с ожидаемой доходностью ?_АВ и риском ст_ав. По правилам, изложенным в предыдущем разделе, соста­вим оптимальный портфель из ценной бумаги А В и тре­тьей акции С. Полученный в результате этого портфель будем рассматривать как ценную бумагу ЛВС с ожидаемой

доходностью г две и риском а авс- Присоединив к ней че­твертую акцию П, составим оптимальный портфель ЛВС О и т. д.

35

зо

25 20

з 2

Рис. 5.12 иллюст­рирует зависимость доходности составляе­мого таким образом портфеля от его риска. Линия 1 — это мно­жество всевозможных

комбинаций г_р, (т_р

о

15

20

10

Рис. 5.12. Область выбора инвестора при