3. Мощность в разветвленных цепях при наличии взаимной индуктивности

Пример 4.21. Составим баланс мощностей для электрической цепи, представленной на рисунке 4.27 и рассмотренной в примерах 4.17 и 4.19.

Из примера 4.17, следует, что комплексы напряжения на источниках питания В, В, В, а комплексы токов А; А; А; А.

1. Определяем активную и реактивную мощности, генерируемые источниками питания.

ВА,

ВА,

ВА.

Суммарная комплексная мощность, генерируемая источниками питания

ВА.

Таким образом, суммарная активная и суммарная реактивная мощности равны Вт, ВАр.

2. Определяем активную мощность, потребляемую потребителями

.

На резистивных элементах

Вт,

Вт,

Вт,

Вт.

Суммарная активная мощность

Вт.

3. Комплексная мощность, передаваемая электромагнитным путем от первой катушки ко второй и от третьей катушки к четвертой

Вт, ВАр

Вт, ВАр.

4. Определяем реактивную мощность, потребляемую потребителями

.

На резистивных элементах

ВАр,

ВАр,

ВАр,

ВАр.

Суммарная активная мощность

ВАр.

5. Баланс реактивных мощностей

ВАр.

4.5. Эквивалентная замена (развязка) индуктивной связи

Анализ и расчет цепей в ряде случаев упрощается, если часть схемы, содержащую индуктивную связь заменить эквивалентной схемой без индуктивной связи. Этот процесс называется эквивалентной заменой, устранением или развязкой индуктивной связи.

На рисунке 4.32,а приведена часть электрической цепи, подсоединенная к узлу 3 и содержащая индуктивно связанные катушки, когда элементы подключены к узлу одноименными зажимами. Используя первый и второй законы Кирхгофа, запишем уравнения, описывающие состояние приведенной части цепи.

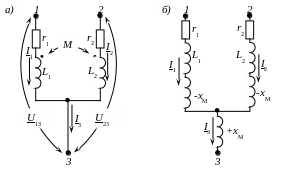
Рисунок 4.32 – Развязка индуктивной связи при подключении элементов одноименными зажимами

Применяя первый закон Кирхгофа для узла 3, имеем .

Применяя второй закон Кирхгофа, определяем напряжение между зажимами 1 и 3, имеем

.

Применяя второй закон Кирхгофа, определяем напряжение между зажимами 2 и 3, имеем

.

Так как , тогда напряжение соответственно равно

.

Так как , тогда напряжение соответственно равно

.

Полученной системе уравнений соответствует схема, приведенная на рисунке 4.32 б. Она не имеет индуктивных связей, т.к. описывается одинаковой системой уравнений. Тогда, полученная система уравнений эквивалентна приведенной выше и, следовательно, описывает состояние цепи.

Таким образом, для устранения индуктивной связи необходимо к катушкам и , подключенных к одному узлу одноименными зажимами, добавить , а перед узлом 3 включить новый элемент .

Если индуктивно связанные элементы, подсоединены к узлу разноименными зажимами (рис. 4.33,а), то для устранения индуктивной связи необходимо к катушкам и добавить , а перед узлом 3 включить новый элемент (рис. 4.33,б).

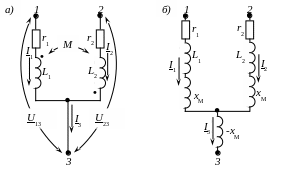
Рисунок 4.34 – Развязка индуктивной связи при подключении элементов разноименными зажимами

В этом случае, напряжения и соответственно равны

,

.

Правило знаков: Если индуктивно связанные катушки подключены к одному узлу одноименными зажимами, то в эти ветви вводится со знаком «-», а в общую ветвь – со знаком «+», и наоборот, если индуктивно связанные катушки подключены к одному узлу разноименными зажимами, то в эти ветви вводится со знаком «+», а в общую ветвь – со знаком «-».

Если индуктивно связанные ветви не имеют общего узла, то развязка индуктивной связи также возможна, однако в данном случае эквивалентная схема получается достаточно сложной и пользоваться ею обычно нецелесообразно.

Если индуктивно связанные элементы соединены трехлучевой звездой или треугольником (рис. 4. 35), то применяя последовательно рассмотренной способ замены, можно перейти к схемам без индуктивных связей.

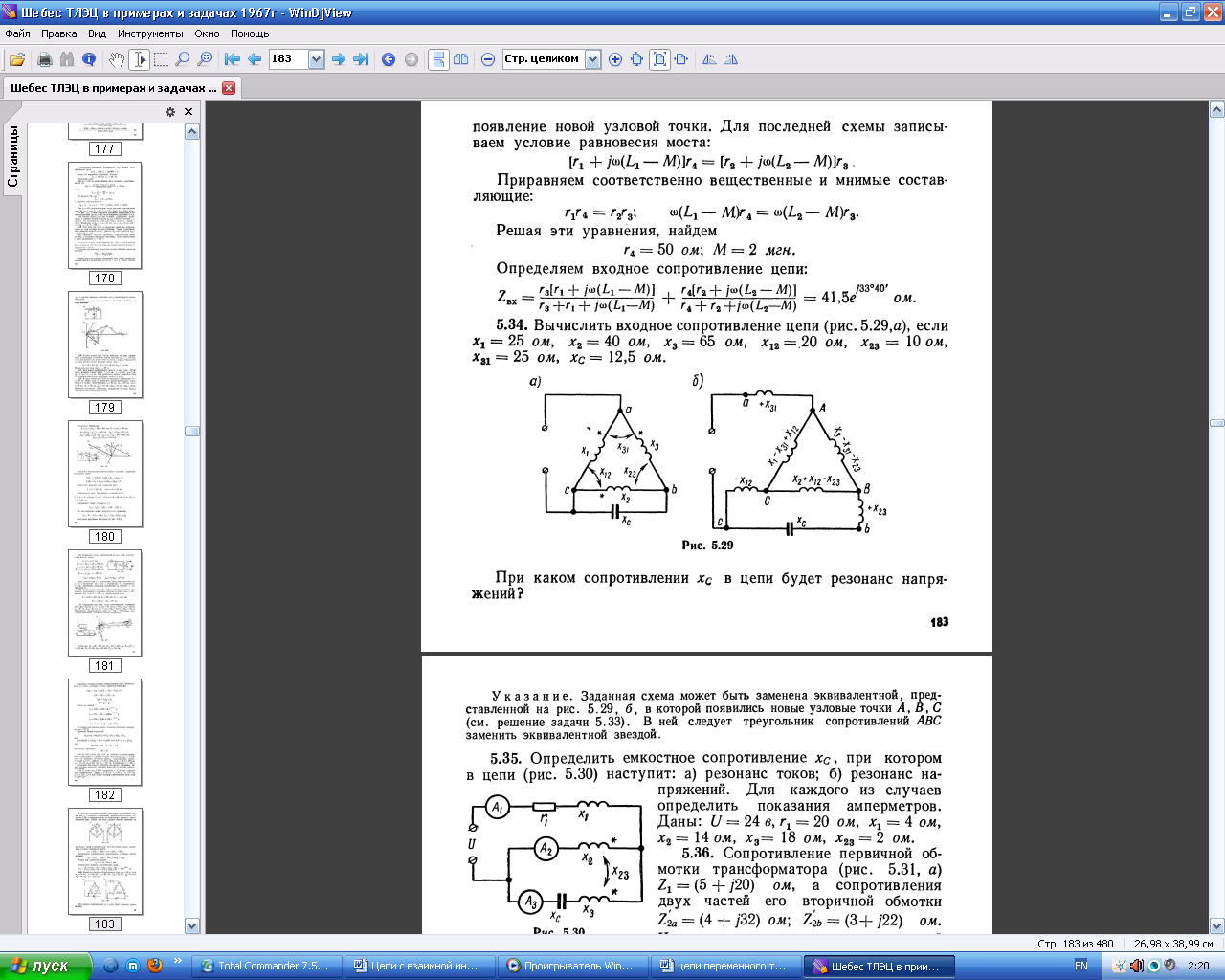
Рисунок 4.35 – Развязка треугольника

Пример 4.23. Рассчитать токи в ветвях индуктивно-связанной цепи, приведенной на рисунке 4.29 и рассмотренной в примерах 4.18 и 4.20, используя эквивалентную замену индуктивных связей.