Решение
Состояние электрической цепи определяется на основании законов Кирхгофа.
1. Составляем систему уравнений по законам Кирхгофа.
1.1. По 1-му закону Кирхгофа:
(1
узел).
1.2. По 2-му закону Кирхгофа:
(I
контур);
(II
контур).
2. Подготовим схему для расчета комплексов тока:
Формируем комплекс ЭДС источника питания:
В.
Формируем комплексные сопротивления ветвей:
Ом;
Ом;
Ом;
Ом.
3. Записываем систему уравнений по законам Кирхгофа в символической форме.
4. Подставляем числовые значения в полученную систему уравнений:
5. Решая данную систему уравнений, определяем токи в ветвях:
А;
А;
А.
Применение метода контурных токов для расчета разветвленных цепей при наличии взаимной индуктивности
При составлении уравнений с использованием метода контурных токов, необходимо учитывать включение индуктивно-связанных катушек относительно контурных токов.
Запишем уравнения для контурных токов (рис. 4.29).
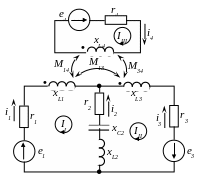
Рисунок 4.29 -
.
.
.
Таким образом, сопротивление взаимной индуктивности входит со знаком плюс или минус в зависимости от того совпадают или не совпадают по отношению к одноименным зажимам направления обхода (или контурного тока) одного элемента и тока в другом элементе.
Пример 4.19. Рассчитать состояние цепи, приведенной на рисунке 4.30 и рассмотренной в примере 4.17, методом контурных токов.
Решение
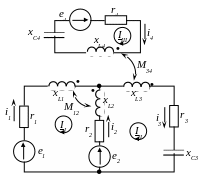
Рисунок 4.30 – Схема для расчета контурных комплексных токов
1.
Приведенная электрическая схема состоит
из четырех ветвей, причем катушки в
первой
и второй
ветвях включены
встречно, а контурные токи
и
направлены навстречу друг другу. Катушки
в третьей
и четвертой
ветвях включены
согласно, а контурные токи
и
направлены навстречу друг другу
2.1. Составляем уравнения для определения контурных токов:
(I
контур);
(II
контур);
(III
контур).
Записываем уравнения в символической форме
;
;
.
2.2. Подставляем числовые значения и решаем систему уравнений:
2.2.1. Контурные сопротивления в символической форме
Ом;
Ом;
Ом.
Сумма сопротивлений, принадлежащих нескольким контурам
Ом;
Ом.
Контурные ЭДС
В;
В;
В.
2.2.2. После подстановки цифровых данных система имеет вид
2.2.3. Решая данную систему уравнений, определяем контурные токи:
А;
А;
А.
2.2.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 4.31.
А;
А;
А;
А.
Токи в ветвях, рассчитанные в примерах 4.19 и 4.17, совпадают.
Пример 4.20. Рассчитать состояние цепи, приведенной на рисунке 4.28 и рассмотренной в примере 4.18, методом контурных токов.
Решение
1. Вычертим схему для определения комплексов тока (рис. 4.31).
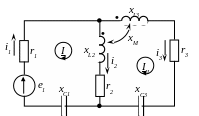
Рисунок 4.31 – Схема для расчета комплексных токов
2.1. Составляем уравнения для определения контурных токов:
(I
контур);
(II
контур).
Записываем уравнения в символической форме
;
.
2.2. Подставляем числовые значения и решаем систему уравнений:
2.2.1. Контурные сопротивления в символической форме
Ом;
Ом.
Сумма сопротивлений, принадлежащих нескольким контурам
Ом.
Контурные
ЭДС
В;
В.
2.2.2. После подстановки цифровых данных система имеет вид
2.2.3. Решая данную систему уравнений, определяем контурные токи:
А;
А.
2.2.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 4.31.
А;
А;
А.
Токи в ветвях, рассчитанные в примерах 4.20 и 4.18, совпадают.