1. Определяем активную и реактивную мощности, генерируемые

источником питания.

ВА.

Таким образом, суммарная активная и суммарная реактивная мощности равны Вт, ВАр.

2. Комплексные мощности, потребляемые каждой параллельной ветвью:

ВА,

ВА.

Таким образом, суммарная активная мощность ветвей Вт, а суммарная реактивная ВАр.

3. Определяем активную мощность, потребляемую потребителями

.

На резистивных элементах

Вт,

Вт.

Суммарная активная мощность

Вт.

4. Комплексная мощность, передаваемая электромагнитным путем от первой катушки ко второй

Вт, ВАр.

Таким образом, активная мощность передается от первой катушки ко второй.

5. Баланс активных мощностей:

Вт,

Вт.

6. Определяем реактивную мощность, потребляемую потребителями

.

На индуктивных элементах

ВАр,

ВАр.

Суммарная реактивная мощность

ВАр.

4. Баланс реактивных мощностей:

ВАр,

ВАр.

4.4. Расчеты разветвленных цепей при наличии взаимной индуктивности

Расчеты разветвленных цепей можно проводить, составляя уравнения по первому и второму законам Кирхгофа или методом контурных токов. Метод узловых потенциалов непригоден, т.к. ток в любой ветви зависит не только от ЭДС, находящегося в ней источника и от потенциалов тех узлов, к которым ветвь присоединена, но и от токов других ветвей, которые наводят ЭДС взаимной индукции. Теорему об активном двухполюснике можно применять только в том случае, когда внешняя по отношению к двухполюснику часть цепи не имеет индуктивных связей с той частью цепи, которая входит в состав двухполюсника. Нельзя пользоваться формулами преобразования, в том числе и треугольника в звезду и наоборот.

При составлении уравнений по второму закону Кирхгофа взаимная индуктивность между элементами k и s учитывается через напряжение на k–ом элементе , причем знак плюс берется в случае, когда направление обхода элемента k и тока совпадают относительно одноименных зажимов.

Для цепей, содержащих индуктивно связанные элементы, справедливо свойство взаимности, доказательство которого ничем не отличается от приведенного для цепей постоянного тока.

1. Применение законов Кирхгофа для расчета разветвленных цепей при наличии взаимной индуктивности

Рассмотрим применение законов Кирхгофа на примере электрической цепи, приведенной на рисунке 4.26.

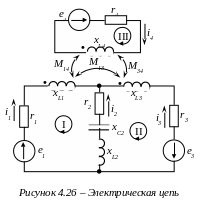
По первому закону Кирхгофа .

По второму закону Кирхгофа для первого контура

.

По второму закону Кирхгофа для второго контура

.

По второму закону Кирхгофа для третьего контура

.

Таким образом, имеем четыре уравнения и четыре неизвестных тока.

Рассмотрим особенности составлений уравнений и расчета разветвленных цепей при наличии взаимной индуктивности на конкретных примерах.

Пример 4.17. Рассчитать состояние цепи, приведенной на рисунке 4.27, методом законов Кирхгофа, если B, B, B, Ом; Ом; Ом; Ом; Ом; Ом; Ом; Ом; Ом; Ом; Ом, Ом.

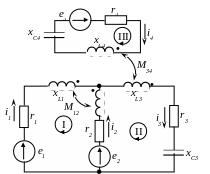
Рисунок 4.27 – Электрическая цепь

Состояние электрической цепи определяется на основании законов Кирхгофа.

1. Составляем систему уравнений по законам Кирхгофа.

1.1. По 1-му закону Кирхгофа:

(1 узел).

1.2. По 2-му закону Кирхгофа:

(I контур);

(II контур);

(III контур).

2. Подготовим схему для расчета комплексов тока:

1. Формируем комплексы ЭДС источников питания:

(В), (В), (В).

2. Формируем комплексные сопротивления ветвей:

Ом;

Ом;

Ом;

Ом;

Ом;

Ом.

3. Записываем систему уравнений по законам Кирхгофа в символической форме.

4. Подставляем числовые значения в полученную систему уравнений:

5. Решая данную систему уравнений, определяем токи в ветвях:

А;

А;

А;

А.

Пример 4.18. Рассчитать состояние цепи, приведенной на рисунке 4.28, методом законов Кирхгофа, если Ом; Ом; Ом; Ом; Ом; Ом; Ом; Ом, В.

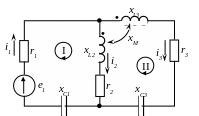
Рисунок 4.28 – Электрическая цепь