Параллельное соединение индуктивно связанных элементов цепи
Предположим, что две индуктивно связанные катушки соединены параллельно. Их параметры соответственно равны: активные сопротивления r1 и r2, индуктивности L1 и L2 и взаимной индуктивностью М. Возможны два вида их соединения – согласное и встречное.
Согласное включение
Одноименные зажимы подключены к одному узлу (рис. 4.18). При положительных направлениях токов и напряжений, указанных на рисунке 4.18, на основании законов Кирхгофа имеем:
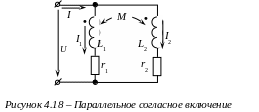
При положительных направлениях токов и напряжений, указанных на рисунке 4.18, на основании законов Кирхгофа имеем:
,
где
,
,
.
Решив эти уравнения, получаем
,
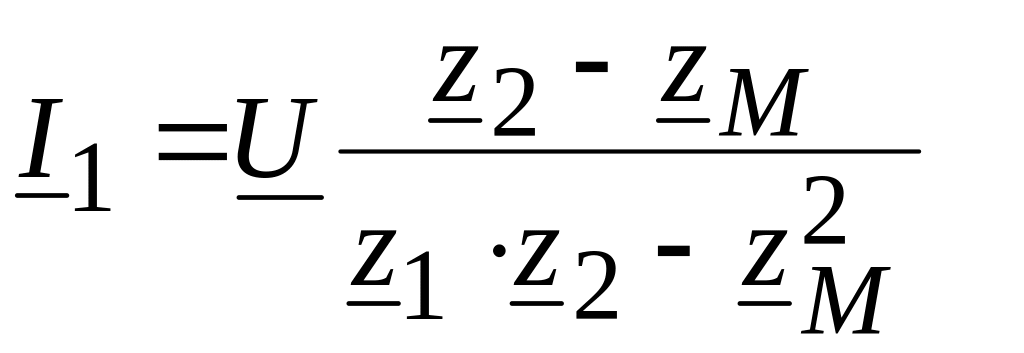
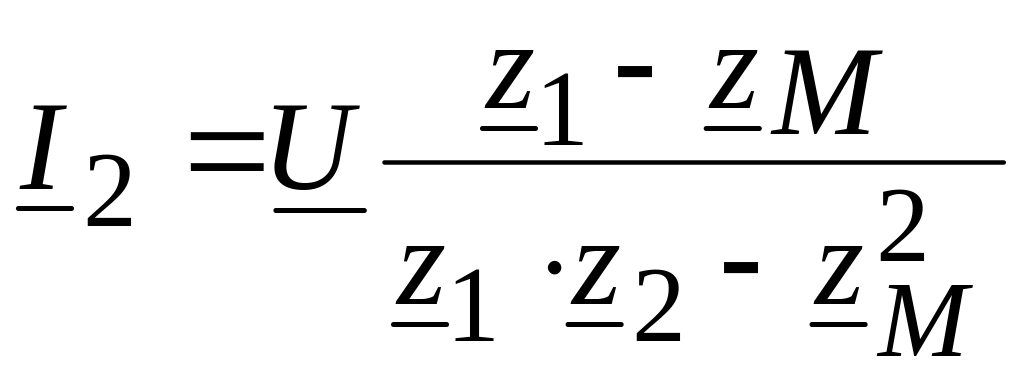
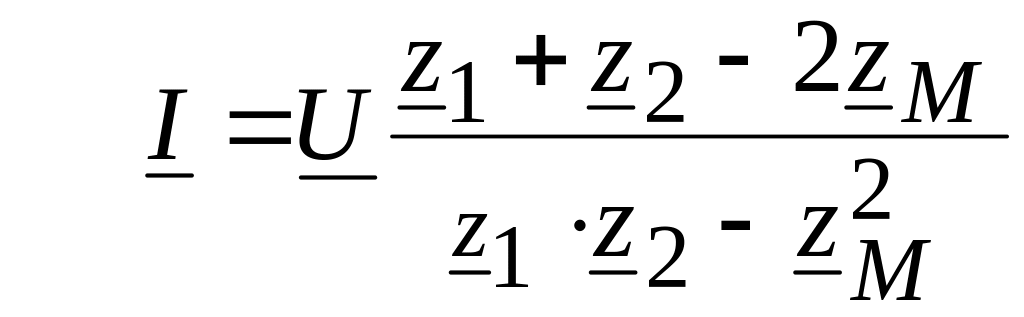откуда
следует, что входное сопротивление цепи
.
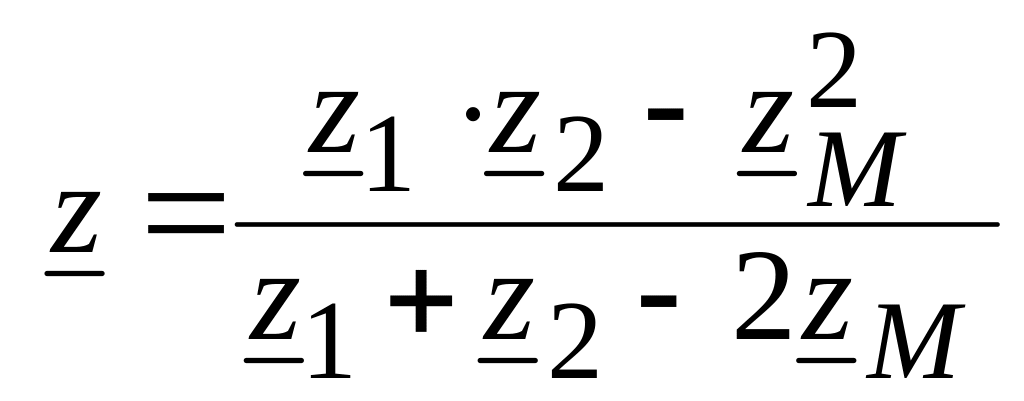При
согласном включении и равных полных
сопротивлениях
:
,
,
откуда
следует, что входное
сопротивление цепи
.
Таким образом, при согласном включении и равенстве полных сопротивлений, ток будет меньше, чем при отсутствии индуктивной связи.
При
,
т.е. при отсутствии индуктивной связи
между ветвями, входное комплексное
сопротивление имеет вид
.
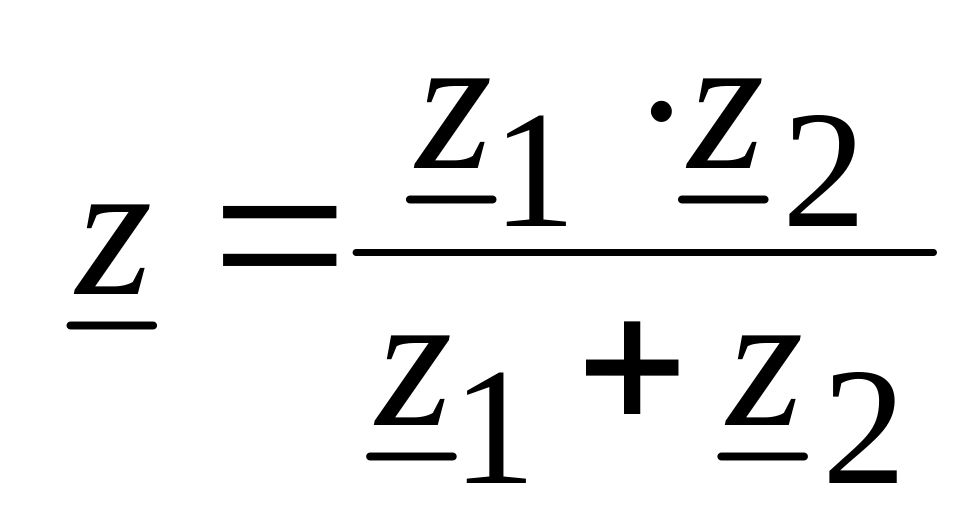Векторная диаграмма при согласном включении, приведена на рисунке 4.19.
Пример 4.9. Цепь состоит из двух одинаковых индуктивно связанных катушек, соединенных параллельно (рис. 4.18), с параметрами r1 = r2 = r = 40 Ом, x1 = x2 = x = 60 Ом, xM = 50 Ом, u = 100 В. Требуется рассчитать токи и напряжения на каждой катушке, ток в неразветвленном участке цепи, построить векторную диаграмму.
Решение.
Определяем сопротивление взаимной индукции:
Ом.
Определяем сопротивление каждой индуктивно связанной катушки:
Ом.
Определяем входное сопротивление цепи:
Ом.
Ток в цепи
A.
Токи в параллельных ветвях
А.
Определяем комплексы напряжений на каждом элементе цепи:
В,
В,
В,
В,
В.
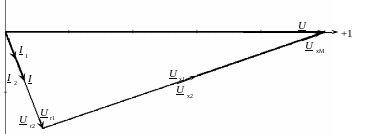
Рисунок 4.20 – Векторная диаграмма при согласном включении двух одинаковых катушек
Пример 4.10. Цепь состоит из двух индуктивно связанных катушек, соединенных параллельно (рис. 4.18), с параметрами r1 = 30 Ом, x1 = 60 Ом, r2 = 100 Ом, x2 = 40 Ом, xM = 20 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму.
Решение.
Определяем сопротивление взаимной индукции:
Ом.
Определяем сопротивление каждой индуктивно связанной катушки:
Ом,
Ом.
Определяем входное сопротивление цепи:
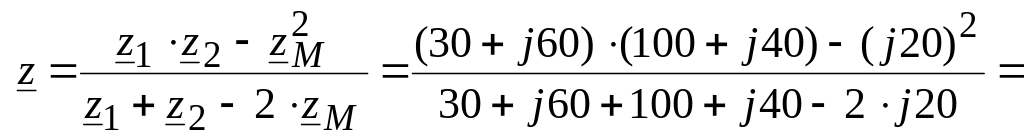
Ом.
Ток в цепи
A.
Токи в параллельных ветвях
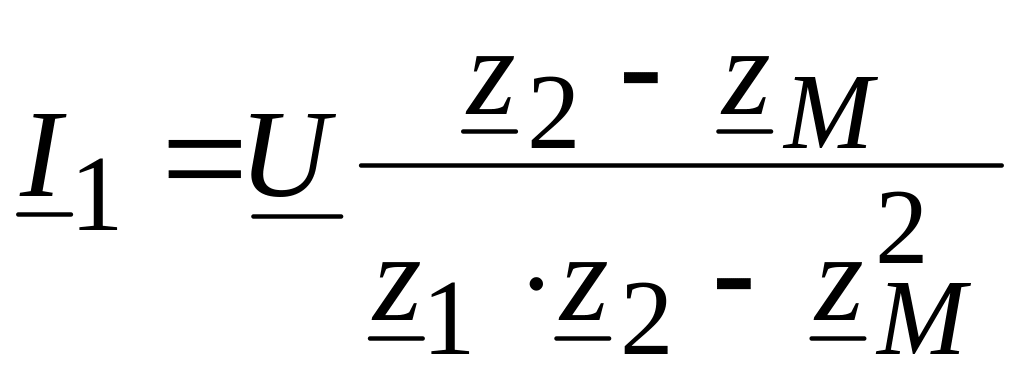
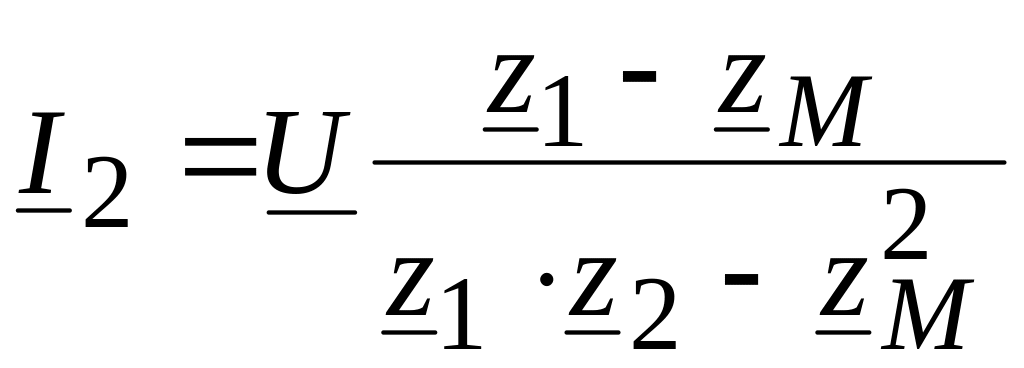
А,
А.
Определяем комплексы напряжений на каждом элементе цепи:
В,
В,
В,
В,
В.
В
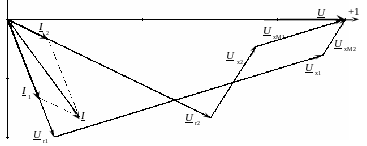
Рисунок 4.21 – Векторная диаграмма при согласном включении двух катушек
Встречное включение
Рассмотрим пример встречного включения. Одноименные зажимы присоединены к разным узлам, т.е. L1 и L2 присоединены к узлу разноименными зажимами (рис. 4.22). тогда положительные направления напряжений взаимной индукции и токов, ориентированы относительно одноименных зажимов неодинаково.
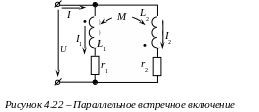
При положительных направлениях токов и напряжений, указанных на рисунке 4.22, на основании законов Кирхгофа имеем:
.
Решив эти уравнения, получаем
,
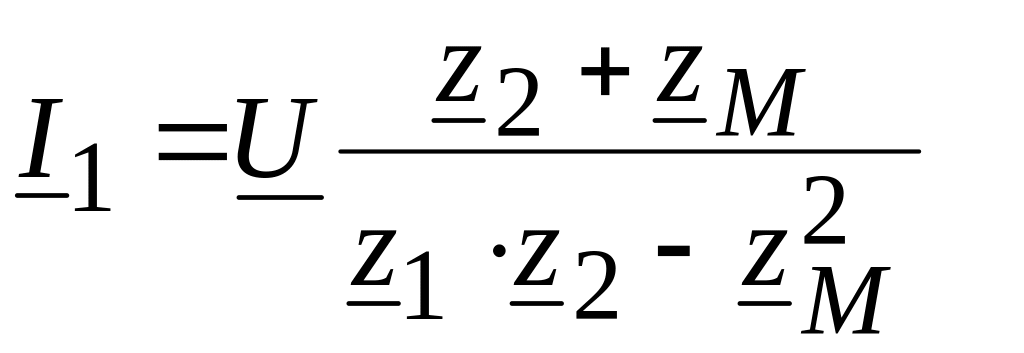
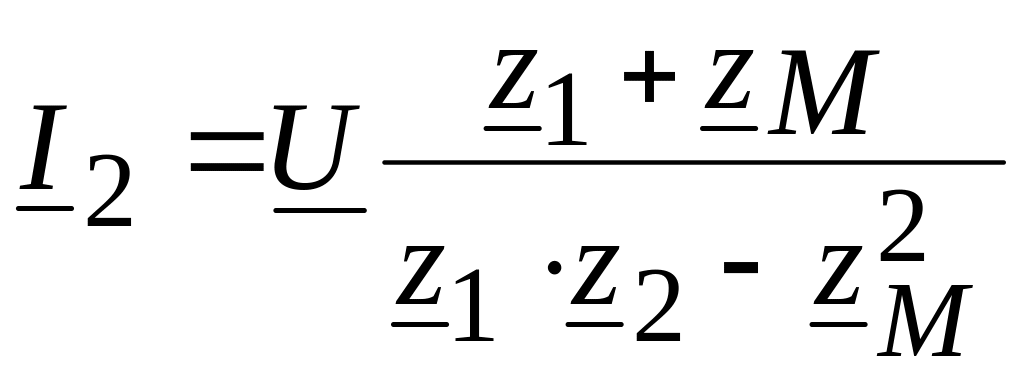
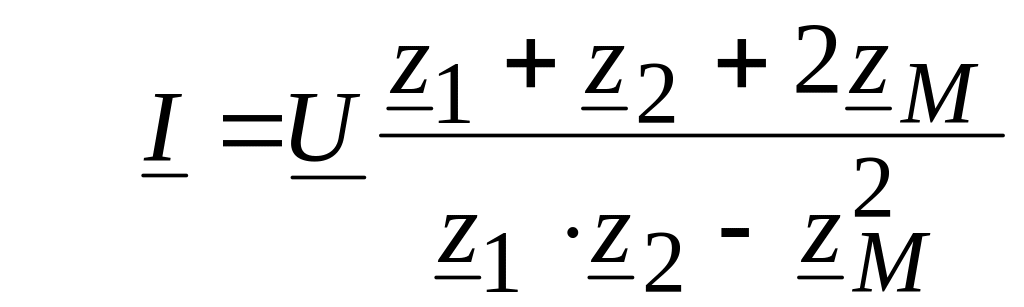откуда
следует, что входное сопротивление цепи
.
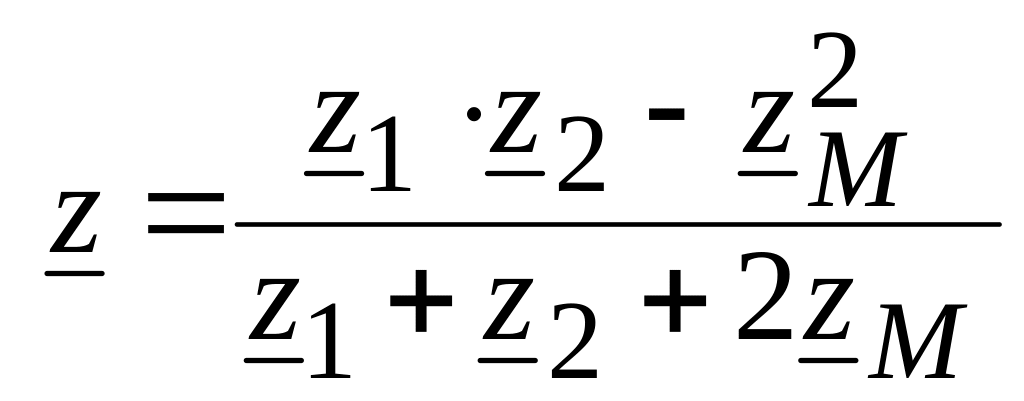При встречном включении и равных полных сопротивлениях :
,
,
откуда
следует, что входное сопротивление цепи
.
Таким образом, при согласном включении и равенстве полных сопротивлений, ток будет больше, чем при отсутствии индуктивной связи.
Векторная диаграмма при согласном включении, приведена на рисунке 4.23.
Рисунок 4.23 – Векторная диаграмма при встречном включении
Пример 4.11. Цепь состоит из двух одинаковых индуктивно связанных катушек, соединенных параллельно (рис. 4.22), с параметрами r1 = r2 = r = 40 Ом, x1 = x2 = x = 60 Ом, xM = 50 Ом, u = 100 В. Требуется рассчитать токи и напряжения на каждой катушке, ток в неразветвленном участке цепи, построить векторную диаграмму.
Решение.
Определяем сопротивление взаимной индукции:
Ом.
Определяем сопротивление каждой индуктивно связанной катушки:
Ом.
Определяем входное сопротивление цепи:
Ом.
Ток в цепи
A.
Токи в параллельных ветвях
А.
Определяем комплексы напряжений на каждом элементе цепи:
В,
В,
В,
В,
В.
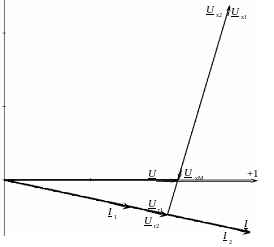
Рисунок 4.24 – Векторная диаграмма при согласном включении двух одинаковых катушек
Пример 4.12. Цепь состоит из двух индуктивно связанных катушек, соединенных параллельно (рис. 4.18), с параметрами r1 = 30 Ом, x1 = 60 Ом, r2 = 100 Ом, x2 = 40 Ом, xM = 20 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму.
Решение.
Определяем сопротивление взаимной индукции:
Ом.
Определяем сопротивление каждой индуктивно связанной катушки:
Ом,
Ом.
Определяем входное сопротивление цепи:
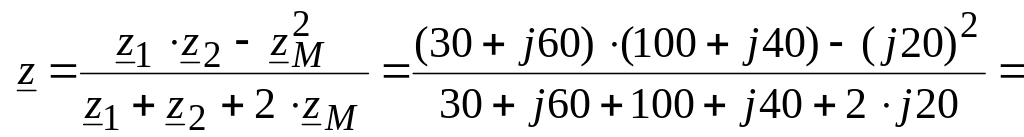
Ом.
Ток в цепи
A.
Токи в параллельных ветвях
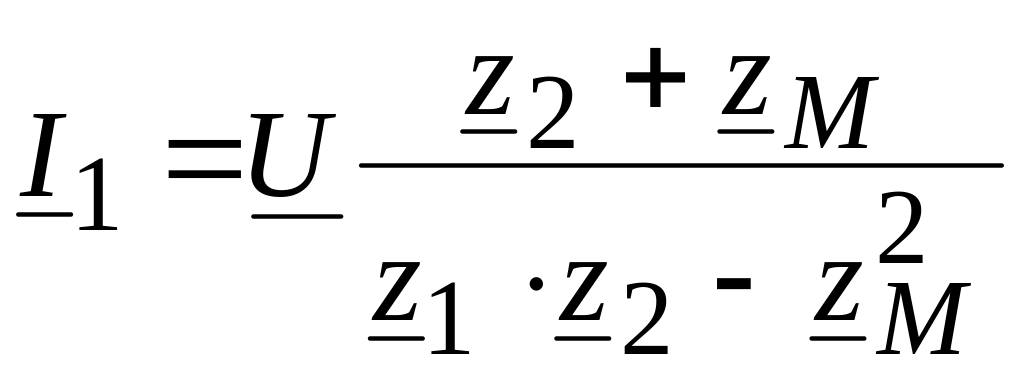
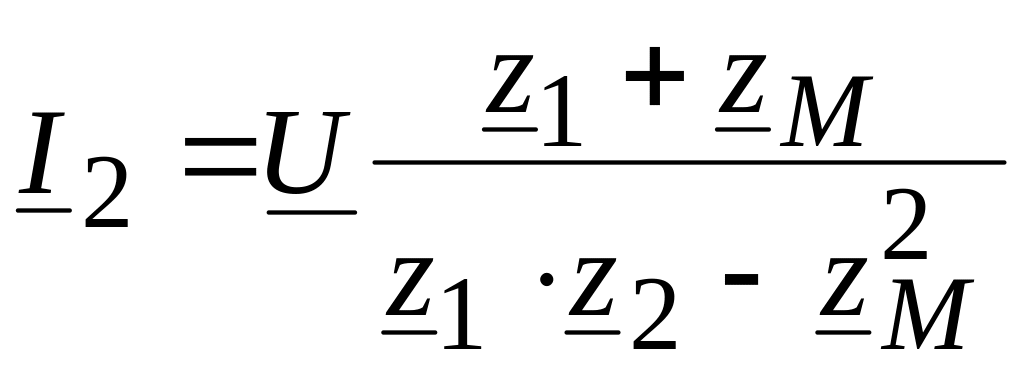
А,
А.
Определяем комплексы напряжений на каждом элементе цепи:
В,
В,
В,
В,
В.
В
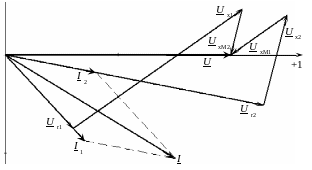
Рисунок 4.25 – Векторная диаграмма при согласном включении двух катушек