§3. Основы теории подъема жидкости в скважине

При восходящем движении газожидкостной смеси в насосно-компрессорных трубах (НКТ) более легкий газ опережает жидкость. Разность средних объемных скоростей движения газа и жидкости называется относительной скоростью. Ее значение зависит от свойств газа и жидкости, скорости смеси, газонасыщенности, и при стесненных условиях движения смеси в НКТ она может быть высокой.

Скорость всплытия одиночных пузырьков газа в сосуде не­ограниченного диаметра определяется свойствами газа и жидкости и линейными размерами пузырьков (рис. VII.5). Для пузырьков малого размера, имеющих сферическую форму, она возрастает пропорционально квадрату диаметра пузырька (за­кон Стока). С увеличением размеров пузырьков форма их ме­няется, скорость всплытия их при этом возрастает медленнее. Наступает момент, когда силы поверхностного натяжения не

Ю Заказ n° 3597 ¹⁴⁵

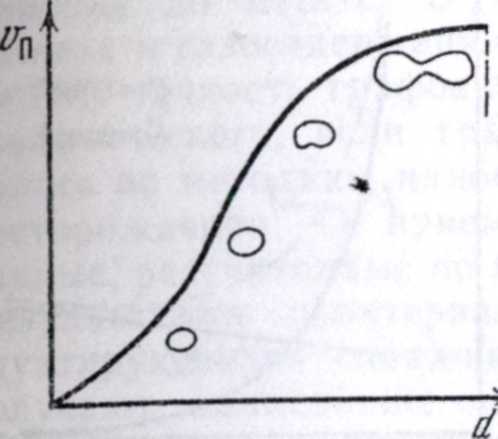
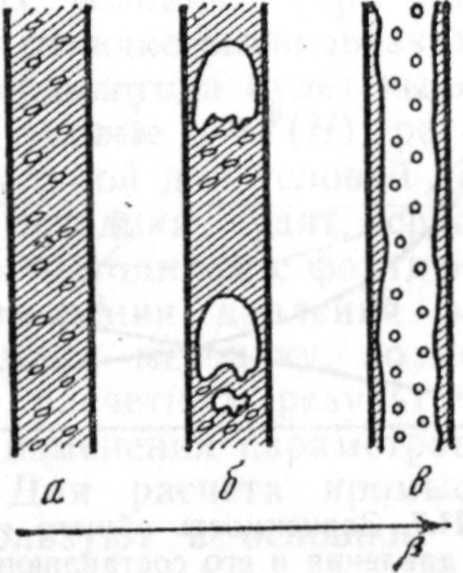
Рис. VI 1.5. Зависимость скорости всплытия пузырька газа в жидкости от его линейного размера

Рис. VI1.6. Структура газожидкостной смеси при восходящем ее движении в трубах

могут сохранить целостность пузырьков. Происходит их дроб­ление, и более мелкие всплывают с несколько меньшей скоро­стью.

Итак, максимальная скорость всплытия одиночных пузырь­ков газа в жидкости ограничена и зависит от свойств и газа, и жидкости. Например, максимальная скорость всплытия пу­зырьков воздуха в дистиллированной воде порядка 26 см/с, а газа в нефти обычно не превышает 20 см/с.

В добывающих скважинах на поток газожидкостной смеси влияют размеры НКТ. При малой газонасыщенности пузырьки газа находятся на некотором расстоянии друг от друга (пузырь­ковая структура, рис. VII.6,a). Их формы и размеры определя­ются соотношениями между силами сопротивления и поверхно­стного натяжения. Относительная скорость при этой структуре

не превышает 10—20 см/с.

С ростом газонасыщенности при определенных свойствах газа и жидкости происходит слияние пузырьков. В этом случае диаметр их практически равен диаметру труб и развивается не­точная (пробковая) структура (см. рис. VII.6,6). Относитель­ная скорость газа достигает 50—100 см/с.

При дальнейшем увеличении газонасыщенности пузырьки сливаются и образуется кольцевая структура или структура тумана (см. рис. VII.6,e). Часть жидкости переносится потоком газа в виде капель, -часть движется вдоль стенки трубы, увле­каемая газом за счет сил трения. Относительная скорость при такой структуре течения может быть значительной (достигать десятков метров в секунду) и небольшой (когда толщина коль­цевого слоя жидкости на стенках трубы незначительна и жидкость переносится в основном потоком газа в виде мель­чайших капель). Помимо указанных структур можно выделить также и промежуточные виды. Вид структуры зависит не только от газонасыщенности, но и от скоростей фаз и свойств жидкости и газа.

Различают два вида газонасыщенности: расходную р— отношение объемного расхода газа к расходу смеси при данных термодинамических условиях и истинную ф — это отношение средней площади трубы, занятой газом, к площади сечения трубы. Если бы газ и жидкость двигались с одинаковой скоро­стью, то ф была бы равна р. В восходящем потоке смеси газ движется с большей скоростью, поэтому ф<р, и тем меньше, чем больше относительная скорость. Действительно, газ при одинаковом расходе, двигаясь с большей скоростью, занимает меньшую площадь сечения трубы.

Итак, с ростом относительной скорости уменьшается содер­жание газа в смеси, а это ведет к увеличению ее плотности.

Впервые дифференциальное уравнение движения газожидко­стной смеси получил Верслуис в 1930 г. При его выводе ско­рости жидкой и газовой фаз принимались одинаковыми. В 1933 г. А. П. Крылов вывел уравнение движения, в котором учитывал различие в скоростях фаз.

В дифференциальных уравнениях движения газожидкост­ных смесей по трубам учитываются разнообразные процессы и явления (массо- и теплообмен между фазами, процессы на границе раздела фаз и т. д.). Не все из них можно проинтегри­ровать в общем виде, но при наличии ЭВМ их решение не вы­зывает затруднений. И все-таки проблема расчета движения га­зожидкостных смесей окончательно не решена, так как в урав­нениях остаются два параметра, которые нельзя определить теоретически: один из них характеризует потери энергии на преодоление массы столба смеси, другой — на трение.

Для решения проблемы определения потерь на трение при движении по трубам однофазного потока потребовались труды сотен исследователей в течение ряда десятилетий. В резуль­тате была получена зависимость коэффициента гидравличе­ского сопротивления от числа Рейнольдса. Универсальная зависимость для коэффициента, характеризующего гидравличе­ские потери при движении газожидкостной смеси, пока не най­дена. То же самое можно сказать об относительной скорости газа в потоке смеси. Эта скорость или определяемая ею истин­ная газонасыщенность зависит от скорости движения смеси и свойств газа и жидкости, последние, в свою очередь, являются функцией давления и температуры. Вывод уравнений расчета коэффициента истинной газонасыщенности осложняется процес­сами коалесценции и диспергирования пузырьков газа при дви­жении смеси. На эти процессы влияет содержание в жидкости поверхностно-активных веществ, учесть которые очень трудно. Эти вещества также влияют и на условия перехода от одной структуры к другой в процессе движения смеси, т. е. на гидрав­лические потери.

Для определения составляющих потерь давления на преодо­ление массы столба смеси и на трение используют эмпириче­ские зависимости, полученные при обработке данных промысло­вых или лабораторных исследований. * В уравнении движения газожидкостной смеси пренебрегают потерями давления на ус­корение и потерями, имеющими еще меньшее значение. Такое уравнение имеет вид

dp ---= ikvgdli -I- Jp_TP, (VII .4)

где dp — общие потери давления по длине подъемника dh\ р<м—плотность смеси; g—ускорение свободного падения; dp_Tp— потери давления на трение. Условия проведения экспери­ментов обычно не одинаковы, различны также и методы интер­претации данных исследований. Поэтому методики расчета движения газожидкостных смесей отличаются друг от

друга. \ ^кы*^ <r Т1^:>'1 йон'п

При расчете промысловых газожидкостных подъемников наиболее распространены в нашей стране методики А. П. Кры­лова— Г. С. Лутошкина, из зарубежных: Поэтмана и Карпен-тера, Данса и Роса, Оркишевского. Эти методики, к сожале­нию, не универсальны, и поэтому при использовании любой из них необходимо учитывать условия месторождения, для чего обычно сравнивают расчетные кривые изменения давления вдоль лифта с фактическими, полученными поинтервальными измере­ниями давления в эксплуатирующихся скважинах.

Цель расчета промысловых газожидкостных подъемников — выбор оборудования и установление режима эксплуатации скважин при различных способах эксплуатации. Необходимость расчета подтверждается данными анализа зависимости потерь давления от диаметра, дебита жидкости и расхода газа. Пере­пишем уравнение (VII.4) в безразмерном виде:

_!_ jЈ_ ₌ _Рс^ ₊ _!_ _{( (VII 5)}

Рж£ dh р_ж Рж£ dh

где р_ж — плотность жидкости.

В левой части этого уравнения приведены общие потери энергии, в правой—потери энергии на преодоление массы

столба смеси и на трение.

Рассмотрим изменение общих потерь энергии в функции рас­хода газа V при подъеме жидкости с заданным дебитом q по трубам диаметром d (рис. VII.7). Увеличение расхода газа ве­дет к росту скорости смеси, а следовательно, и потерь на тре­ние dprplpngdh (см. рис. VII.7, кривая /), а также к увеличе­нию истинной газонасыщенности смеси и уменьшению ее плот­ности, т. е. к уменьшению первого слагаемого в правой части уравнения (VII.5) (см. рис. VII.7, кривая 2).

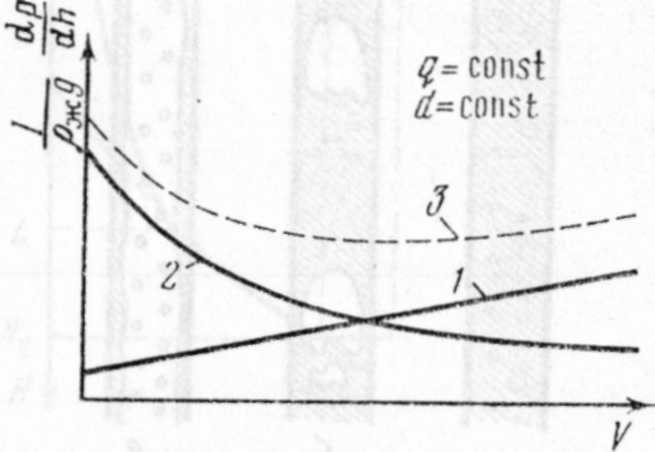
Рис. VI 1.7. Зависимость общего гра­диента давления и его составляющих от расхода газа при постоянных ди­аметре НКТ и дебите жидкости

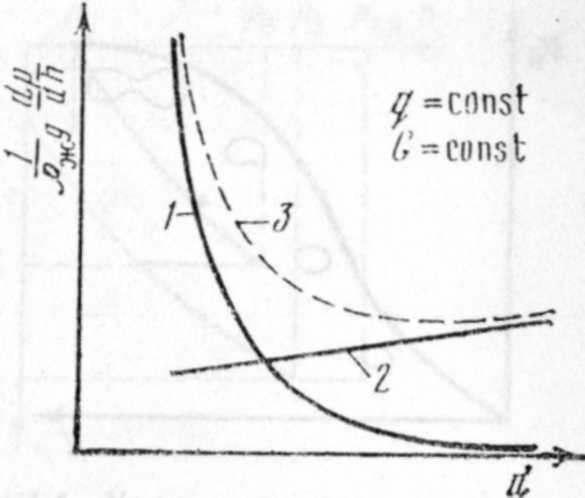
Рис. VI 1.8. Зависимость потерь энергии от диаметра подъемника при заданных расходах жидкости q и га­зовом факторе

Если газонасыщенность незначительная, течение смеси про­исходит при пузырьковой структуре и небольшой относительной скорости движения газа. В этом случае увеличение расхода газа приводит к значительному уменьшению плотности. С ро­стом газонасыщенности относительная скорость повышается (пробковая, кольцевая структуры), поэтому возрастание рас­хода газа влияет в меньшей степени на плотность смеси (кри­вая 2 на рис. VII.7 выполаживается).

Зависимость общих затрат энергии от расхода газа получим, складывая кривые / и 2. Результирующая кривая 3 на рис. VI 1.7 имеет минимум. При малой газонасыщенности потока вследст­вие увеличения расхода газа первое слагаемое в правой части уравнения (VII.5) уменьшается быстрее, чем растет второе; при значительной газонасыщенности, наоборот, с возрастанием расхода газа потери на трение растут интенсивнее, чем умень­шаются потери энергии на преодоление массы столба смеси. В результате суммарные потерн возрастают.

Итак, можно подобрать такой расход газа, который обеспе­чит подъем жидкости с заданным дебитом через трубы данного диаметра при минимальных затратах энергии (т. е. при мини­мальном градиенте давления). Это — главное условие выбора режима работы газожидкостного подъемника, особенно при газ-лифтном способе эксплуатации.

Рассмотрим зависимость общих потерь энергии от диаметра подъемника при заданных расходах жидкости и газа (рис. VII.8). Если диаметр подъемника небольшой, расход энергии мо­жет быть высоким вследствие больших потерь на трение. При постоянном дебите смеси потери давления на трение прибли­женно обратно пропорциональны пятой степени диаметра подъ­емника. Поэтому с увеличением диаметра они сначала резко уменьшаются, а затем темп их изменения становится более шающих 20 мПа-с. В аномальных условиях (при больших дебитах и газосодержаниях или при откачке высоковязких жид­костей) точность графоаналитического метода будет выше, чем аналитического, если градиентные кривые р = ((Н) рассчиты­вались по методику, наиболее приемлемой для условий данного месторождения. О приемлемости методики судят, сравнивая данные, рассчитанные по нескольким методикам с фактическими результатами поинтервального измерения давления в экс­плуатирующихся скважинах. Выбирают методику, по которой получают наименьшие отклонения расчетных результатов от фактических в широком диапазоне изменения параметров сква­жин на данном месторождении. Для расчета промысловых газожидкостных подъемников используют в основном графо­аналитический метод.

Следует отметить, что название методов несколько условно, так как раньше для решения многих задач с применением формул А. П. Крылова пользовались графиками. В последнее время для промысловых расчетов широко используют ЭВМ. В машину вводится программа расчета по данной методике в виде аналитических и табличных зависимостей, характери­стика пласта и скважин, а ЭВМ дает уже готовые рекомендации по выбору оборудования и установления оптимального режима эксплуатации скважин. Тем не менее в дальнейшем для на­глядности и возможности анализа нами будут показаны после­довательность и промежуточные результаты решения промыс­ловых задач, где широко применяют графические методы ре­шения и построения.

По выбранной для данного месторождения методике строят градиентные кривые p = f(H) для НКТ различного диаметра при движении по ним продукции скважин с разными дебитами и обводненностью. Если скважины эксплуатируются газлифт-ным способом, во время построения градиентных кривых учи­тывают и различные газожидкостные отношения.

Для расчетов необходимо иметь результаты исследования пластовых нефтей. На рис. VII.9 показаны зависимости свойств нефти и газа от давления, значение объемного коэффициента нефти в, количества выделившегося V_rn и растворенного V_rp газа, приходящегося на 1 т нефти, в функции давления. Эти кривые различны для каждого месторождения и определяются

экспериментально.

Как уже отмечалось, в основу многочисленных методик расчета движения газожидкостных смесей по вертикальным трубам положено дифференциальное уравнение баланса дав­ления:

_ Jt. - p_CMg + Pc_Mg + Рс* if -. (VI1.8)

Ah an an

где dp —изменение давления на длине трубы dh\ р_см и v —

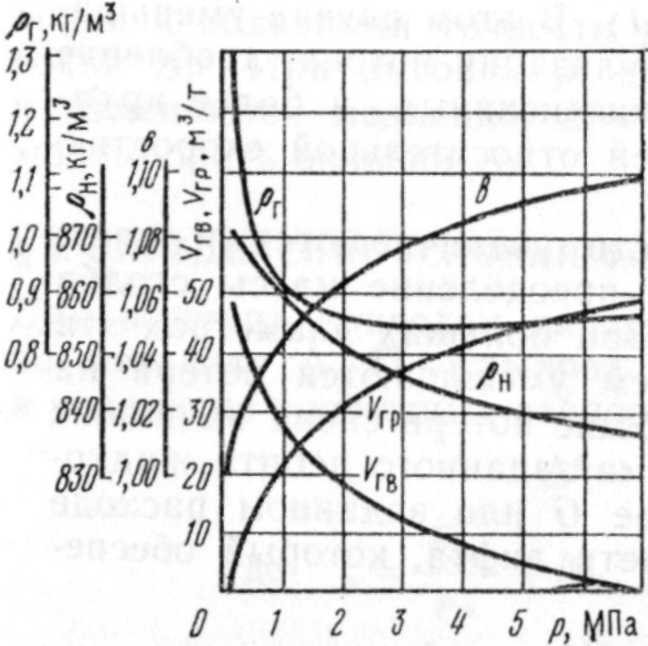
Рис. VI 1.9. Зависимости свойств неф­ти и газа от давления

Рис. VI 1.1(0. Блок-схема расчета на ЭВМ забойного давления в зависи­мости от устьевого

средние значения плотности и скорости смеси на этой длине; g — ускорение свободного падения; dh_TP — потери на трение на длине dh, выраженные в метрах столба смеси. Последнее сла­гаемое отражает потери на ускорение движения смеси.

Существующие методики отличаются конкретными выраже­ниями для определения слагаемых в правой части уравнения (VII.8). Для каждой методики это уравнение (VI 1.8) можно представить в следующем виде:

dp/dh=f(p₉ ft). (VI1.9)

Уравнение (VI 1.9) — нелинейное дифференциальное урав­нение первого порядка. Так как в состав этого уравнения вхо­дят сложные эмпирические функции, аналитически оно не ре­шается. Для решения (VI 1.9) чаще используют численный метод последовательных приближений (метод итерации), сущ­ность которого заключается в следующем: уравнение (VI 1:9) преобразуют в уравнение в конечных разностях, задают числен­ное значение приращения одной из переменных (Ар и Ah) и за­тем методом итерации определяют приращение другой пере­менной. Целесообразнее задаваться значением Ар. Это приводит к уменьшению числа итераций в одной расчетной ступени, вследствие того что параметры уравнений (VII.8) и (VII.9) в большей мере зависят от давления, чем от температуры.

На рис. VII. 10 показана блок-схема расчета забойного дав­медленным (см. рис, VI 1.8, кривая 1). В этом случае уменьша­ются скорость смеси и степень турбулизации потока; дробление пузырьков газа становится менее интенсивным, и более круп­ные пузырьки всплывают с большей относительной скоростью

(см. рис. VII.5). *

С ростом относительной скорости увеличиваются и плот­ность смеси, и расход энергии на преодоление массы столба смеси (см. рис. VII.8, кривая 2). При больших диаметрах эти потери возрастают интенсивнее, чем уменьшаются потери на трение (кривая /). В результате общие потери снова начинают расти (кривая 3). Итак, для подъема заданного дебита жидко­сти при известном газовом факторе G или заданном^ расходе газа можно подобрать такой диаметр лифта, который обеспе­чит минимум расхода давления.