1.23 Теоремы Ферма и Ролля

Е сли ф-я f(x) определена и непрерывна на интервале (a;b), принимает наибольшее (наименьшее) значение в некоторой внутренней т. C и имеет производную в этой т., то эта производная равна 0. Док-во: Пусть ∆x – приращение аргумента в окрестности т. C., f(C) –наибольшее значение, тогда f’(C) = lim [f(C + ∆x) – f(C)]/∆x при ∆x0 (из. опр. произв.) Рассмотрим [f(C + ∆x) – f(C)]/∆x. Очевидно f(C + ∆x) < f(C); [(C + ∆x) – f(C)]<0 Если ∆x>0, то [f(C + ∆x) – f(C)]/∆x<0, но тогда f’(C)≤0, как предел отрицательной ф-ции. Если ∆x<0, то [f(C + ∆x) – f(C)]/∆>0, но тогда f’(C)≥0, как предел положительной ф-ции. Т.к. f’(C) существует и не зависит от значения ∆x, то из условия f’(C)≤0, f’(C)≥0 => f’(C)=0

Геометрическая интерпретация (картинка вверху)

т еорема Ролля: Если ф-я f(x) определена и непрерывна на [a;b], дифференцируема в каждой т. его внутренней точке и f(a) = f(b) (принимает равные значения на концах интервала), то найдётся хоть одна внутренняя т. C, в которой f’(C)=0. Док-во: при док-ве используется теор. Ферма. 1) Пусть наиб. M и наим. M значения ф-ции совпадают (M=m). f(x) = const = M на [a;b]=> любая т. внутри [a;b] удовлетворяет т. Ролля (f’(C)=0) 2) Пусть M>0, тогда хотя бы одно из этих значений достигается во внутренней т. [a;b]. Т.к. на концах интервала значений равны. Пусть M=f(C); C∈ (a;b). Тогда по т. Ферма f’(C)=0. (∃f’(C) определяется условием дифференцируемости на всём (a;b)) Т. Ролля не указывает на кол-во точек C, в которых производная обращается в 0. Она утверждает, что существует одна такая точка. Замечание: нарушение хотя бы одного из условий т. Ролля приводит к тому, что теорема становится неверной.

Нарушение

непрерывности	дифференцируемости	р-во значений

1.25 Правило Лопиталя и его приложение…

1) Если y=f(x) и y= Φ(x) дифференцируемы в некоторой окрестности т. a и lim [xa]f(x) = 0 и lim [xa] Φ(x), то Φ’(x) ≠0 в этой окрестности, то из существования lim [xa]f’(x)/ Φ’(x) => lim [xa]f(x)/ Φ(x) При до-ве правила Лопиталля исп. Теорему Коши. Замечания: фигурирующая в правиле т. а может быть как конечной, так и бесконечно удалённой.

2) При выполнении всех требований прав.1 и условии lim [xa]f(x)= и lim [xa] Φ (x)= имеет место тоже правило вычисления пределов lim [xa]f’(x)/ Φ’(x) => lim [xa]f(x)/ Φ(x). Таким образом решаются неопределённости виды: (0/0), (/),⁰ ,1^, 0⁰,-

Примеры: lim[x0]cosx^(1/x³) = (1^). Представим lim[x0]e^ [lncosx^(1/x³)] = lim[x0]e^ (1/x³) lncosx; e^ lim[x0] lncosx /x³; lim[x0] lncosx /x³ =(0/0)=

lim[x0] [(-sinx)/cosx]/3x²=-1/3 lim[x0]sinx/ x2= -1/3 lim[x0]cosx/2x=-; e^- =0

1.27 Необходимый и достаточный признак экстремума. Схема исследования на экстремумы

п.1 необходимый признак экстремума

о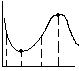 пр.1: Точка x₀ н/з точкой максимума ф-ции f(x), если ∃ U_ɗ(x₀):∀x∈ U_ɗ(x₀) (x≠x₀) f(x)<f(x₀)

опр.2: Точка x₀ н/з точкой минимума ф-ции f(x), если ∃ U_ɗ(x₀):∀x∈ U_ɗ(x₀) (x≠x₀) f(x)>f(x₀)

Т. max и min н/з т. локального экстремума ф-ции.

П.2 Необходимый признак экстремума: Если в. т.x₀ y=f(x)имеет экстремум и в этой т. существует производная, то эта произв. равна 0. Пусть x₀ – т. локального max и ∃ f’(x₀). Тогда рассмотрим U_ɗ(x₀) [x₀ -ɗ; x₀ +ɗ]. y=f(x) достигает наиб. Значения в т. x₀ Кроме того в этой т. выполняется условия теоремы Ферма => в т.x₀ производная равна 0. Это означает, что в этой т. ф-я имеет гориз. Касательную.

П.3 Обобщённый необходимый признак экстремума: Если ф-я y=f(x) имеет в т.x₀ локальный экстремум, то производная в этой т. или равна 0 или не существует. В точке, в которой ф-я непрерывна, а производная либо равна нулю или не существует н/з критическими т. ф-ции (или т. подозрительными га экстремум) Достаточный признак экстремума: Если рпоизводная дифференцируемой ф-ции f(x) припереходе через Крит. Т.x₀ меняет свой знак, то в т.x₀ ф-я y=f(x) имеет экстремум. При этом если меняется с “+” на “-”, то x₀ - т. максимума, если с “-” на “+”, то x₀ - т. минимума. Если знак произв. не меняется в т. x₀ нет экстремума. Док-во: Пусть f’(x) меняет знак с “+” на “-” при переходе через т. x_0. Рассмотрим окрестность т.x₀ вида (x₀-ɗ; x₀), x∈ (x₀-ɗ; x₀). Составим разность f(x) – f(x₀) = f’(ξ)(x- x₀)<0, где ξ∈(x₀-ɗ; x₀) и оценим по т. Лагранжа: x< ξ <x₀; f(x₀) > f(x) ∀x∈U(x₀) ; средняя U(x₀)= (x₀; x + ɗ) Аналогично: f(x) – f(x₀) = f’(ξ)(x- x₀)<0, x> x₀; x∈ среднее U (x₀); f(x₀)> f(x), ∀x∈ среднее U (x₀) А это значит, что x₀ – т. максимума (по определению) Аналогично до-я наличие минимума. Пусть f’(x) при переходе через x₀ не меняет знака. f(x) – f(x₀)= f’(ξ)(x-x₀)<0, f(x) – f(x₀)= f’(ξ)(x-x₀)>0 Замечание: этот признак сохраняется и в случае, когда в т. x₀ ф-я определена и непрерывна, но не дифференцируема. f’(x₀) – не существует, но существует в некоторой окрестности этой т. 2-ой достаточный признак: Если 2-ая производная дважды дифференцируемой ф-ции f(x) в критической т. x₀ положительна, то x₀ - т. min, а если отрицательна, то max. Док-во: Пусть x₀ – Крит. Т. и f”(x₀)>0 Док-ем, что x₀ - т. min. Для этого рассмотрим (1) f”(x)= f’(x₀ + ∆x) – f’(x₀)]/∆x [∆x0] в р-ве (1) f’(x₀) = 0, т.к. x₀ – критическая т., в которой существует производная, тогда (1) => (2) (2) f”(x)= lim {f’(x₀ + ∆x)/∆x}>0 [∆x0] Из теории пределов известно, что если предел положительный, то ф-я положтельная f’(x₀ + ∆x)/∆x>0. Проанализируем эту дробь в зависимости от значения ∆x: ∆x>0 => f’(x₀ + ∆x)>0; ∆x<0 => f’(x₀ + ∆x)<0. Т.е. x₀ – min. Аналогично до-ется max. Замечание: Этим признаком можно пользоваться только, если в т. x₀ существует первая и вторая производные. Схема исследования на экстремумы: 1) решаем Ур-е f’(x)=0 и отбираем корни этого Ур-я, а также т. в которых ф-я определена и непрерывна, но не дифференцируема. 2) Отмечаем на ОДЗ ф-ции все Крит. Т. и используем первый и второй достаточный дост. Признаки экстремума.