
- •1.3 Определение предела функции (для конечной и бесконечно удалённой точек)
- •1.7. Первый замечательный предел (с выводом)
- •1.11 Точки разрыва ф-ции.
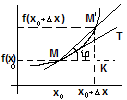
- •1 .15 Определение производной и её геометрический смысл.
- •1.19 Дифференцируемость ф-ции. Теорема о необходимом и достаточном условии дифференцируемости.
- •1.23 Теоремы Ферма и Ролля
- •1.25 Правило Лопиталя и его приложение…
- •1.27 Необходимый и достаточный признак экстремума. Схема исследования на экстремумы
- •2.2 Определение неопределённого интеграла
- •2.6 Методы интегрирования простейших алгебраических дробей
- •2 .10 Определённый интеграл и его геометрический смысл.
- •2.14 Теорема о замене переменной под знаком определённого интеграла.
- •2.18 Длина дуги плоской кривой.
1.3 Определение предела функции (для конечной и бесконечно удалённой точек)
Определение предельной точки: точка a н/з предельной т. множ. X, если в любой сколь угодно малой дельта-окрестности точки a н/х элементы мн. X. Заметим, что т. a может и не быть элементом мн. X.
Если x a, то a – предельная точка мн. X, которому принадлежат значения x.
Если x a+0, то это значит, что x правее a
Если x a-0, то это значит, что x левее a
Введём понятие предела функции:
Пусть f(x) – функц., которая определена в некоторой окрестности т. a, a – предельная т. мн. X ⊃ U (a)
B – lim f (x) (при xa), если ∀ɛ>0 ∃ Uɗ(a): ∀x∈ Uɗ(a), |f(x)-b| < ɛ
∀ɛ>0 ∃ɗɛ > 0, такое что из выполнения неравенства 0 <|x-a|< ɗ =>|f(x)-b|<ɛ
В этом определении ɛ
- произвольно взятая положительная
величина, сколь угодно малая. По выбранному
ɛ
находится ɗ
- положительная величина, зависящая от
выбранного ɛ.
этом определении ɛ
- произвольно взятая положительная
величина, сколь угодно малая. По выбранному
ɛ
находится ɗ
- положительная величина, зависящая от
выбранного ɛ.
Поясним геометрический смысл предела при условии: а – конечная предельная точка.
В![]() озьмем
интервал радиусом ɛ
с центром в т. b
и по заданному ɛ
установим графически ɗ
озьмем
интервал радиусом ɛ
с центром в т. b
и по заданному ɛ
установим графически ɗ
ɗ = min{a-c;d-a}, ∀x∈ Uɗ(a), |f(x)-b|<ɛ
![]()
Пусть a – бесконечно удалённая предельная точка
∀ɛ>0 ∃ Mɛ>0, как только |x| > M =>|f(x)-b|<ɛ
1.7. Первый замечательный предел (с выводом)

lim sinx/x = 1 (x 0) x – в радианах
x>0 x 0, MB = sinx, OB = cosx
Т.к. 0<sinx<x (MB<KM), по т. Sinx0, x0
Cosx 1, x 0
lim cosx (x0)= lim sqr(1- sin2x) = 1
Sock>Somk>Somb
1/2OB*BM < 1/2xR2 < 1/2OK*KC
1/2sinxcosx < 1/2x < 1/2tgx
sinxcosx < x < tgx |: sinx
cosx <x/sinx< 1/cosx
1/cosx > sinx/x > cosx
lim sinx/x = 1 (x 0)
2 случай (x<0, x0)
Заменим x на –x, тогда –x 0 и –x > 0, как следует из предыдущего имеет место неравенство 1/cos(-x) > sin(-x)/(-x) > cos(-x). Используя чётность cosx и нечёт. Sinx: 1/cosx > sinx/x > cosx… lim sinx/x = 1 (x 0) □
1.11 Точки разрыва ф-ции.
1) Т. x0 н/з т. р-ва ф-ции y=f(x), если эта т. принадлежит D(y) или её границе.
2) В этой т. нарушается непрерывность.
По характеру разрыва т. р-ва делятся следующим образом:
1) т. р-ва первого рода
а) точки устранимого р-ва
x0 – т. устранимого р-ва, если односторонние пределы в этой т. конечны и равны, но не равны значению ф-ции в данной точке (которого может и не быть)
y= sin/x, x ≠ 0; x = 0 – т. р-ва
Вычислим односторонние пределы:
Lim sinx/x =1 (x + 0); Lim sinx/x =1 (x - 0), а следовательно они равны => f(x0) – имеет устранимый р-в Можно создать непрерывную всюду ф-ю f(x) ={sinx/x; x ≠ 0 и 1; x=0
б) неустранимый р-в 1-ого рода
x0 – т. неустранимого р-ва 1-ого рода, если односторонние пределы в этой т. конечны, но не равны.
y= sin/|x|, x ≠ 0; x = 0 – т. р-ва
Lim sinx/|x| =1 (x + 0); Lim sinx/x = -1 (x - 0)
Графически неустранимый р-в изображается скачком по оси ординат.
2) Т. р-ва второго рода
x0 – т. р-ва 2-ого рода, если хотя бы один из односторонних пределов в этой т. бесконечны или не существуют.
