2.1 Запись гармонических колебаний в комплексной форме

Рассмотрим в комплексной плоскости радиус- вектор постоянной длины Конец вектора при изменении параметра t (в данном случае t - время) описывает окружность радиуса с центром в начале координат (рис.7)

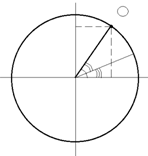
Рис.7

Пусть угол ψ, образованный вектором и осью , выражается так: Величина называется угловой скоростью вращения вектора . Проекции вектора на оси и

, . (7)

Выражения (7) суть решения уравнения (4).

Рассмотрим комплексную величину

Или

(8)

В декартовой системе координат действительную часть комплексного числа обычно откладывают по оси абсцисс, а мнимую - по оси ординат (см. рис.7). Следовательно, любое комплексное число можно представить в виде вектора A на комплексной плоскости, проведенного из начала координат в точку с координатами {x; y}.

Таким образом, решения уравнения гармонических колебаний (4) можно рассматривать как проекции вектора на оси и , вращающегося с угловой скоростью при начальной фазе

Пользуясь формулой Эйлера 

e^iα = cos α +i·sin α,

где i = (-1)^1/2 - мнимая единица, выражение (8) можно переписать так:

(9)

Мнимая и действительная части выражения (9) являются решениями уравнения (4). Выражение (9) называется комплексным решением уравнения (4). Перепишем выражение (9) так:

. (10)

Выражение называют комплексной амплитудой. Обозначим ее через . Тогда комплексное решение (10) перепишется так:

. (11)

4. Пусть . В этом случае корни характеристического уравнения – комплексные числа

где

Общий интеграл имеет вид

(12)

Или

(13)

Здесь в качестве амплитуды приходится рассматривать величину , зависящую от времени. Так как , то она стремится к нулю при , то есть здесь мы имеем дело с затухающими колебаниями. График затухающих колебаний изображен на рис.8.

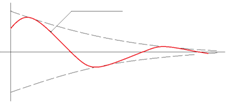
Рис.8

2.2 Запись гармонических колебаний в векторной форме

Гармонические колебания можно изображать с помощью векторных диаграмм. Этот метод состоит в следующем. От начала оси абсцисс проводится вектор А, проекция которого на ось 0X равна Асоs (рис.9).

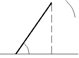
Рис.9

Если вектор А равномерно вращается с угловой скоростью против часовой стрелки, то + _о = , где _о – начальная фаза, и проекция вектора А на ось 0X изменяется со временем по гармоническому закону:

3. Вынужденные колебания. Резонанс

3.1 Вынужденные колебания

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения. После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания свободных колебаний в колебательной системе. В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте и свободные колебания на собственной частоте .

Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте внешней вынуждающей силы. Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 10). Внешняя сила приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 10) конец пружины перемещаться по закону:

где – амплитуда колебаний, – круговая частота.

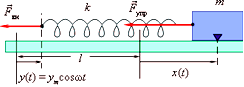
Рис. 10. Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону - длина недеформированной пружины, – жесткость пружины.

Уравнение вынужденных колебаний имеет вид

(1)

Рассмотрим практически важный случай, когда возмущающая внешняя сила является периодической и изменяется по закону

Тогда уравнение (1) примет вид

(1’)

1. Предположим сначала, что и , то есть корни характеристического уравнения – комплексные числа В этом случае (см. формулы (12) и (13) выше) общее решение однородного уравнения имеет вид

(2)

Частное решение неоднородного уравнения ищем в форме

(3)

Подставляя это выражение в исходное дифференциальное уравнение, находим значения и :

Прежде чем подставить найденные значения и в равенство (3), введем новые постоянные и , положив

то есть

Тогда частное решение неоднородного уравнения можно записать в форме

или окончательно

Общий интеграл уравнения (1) равен то есть

Первый член суммы, стоящей в правой части (решение однородного уравнения), представляет затухающие колебания; при увеличение t он убывает, и, следовательно, через некоторый промежуток времени главное значение будет иметь второй член, определяющий вынужденные колебания. Частота этих колебаний равна частоте внешней силы f(t); амплитуда вынужденных колебаний тем больше, чем меньше p и чем ближе к q.

Исследуем подробнее зависимость амплитуды вынужденных колебаний от частоты при различных значениях p. Для этого обозначим амплитуду вынужденных колебаний через :

дифференциальный механический колебание резонанс

Положим ( при p=0 равнялась бы частоте собственных колебаний). Тогда

Введем обозначения

где - отношение частоты возмущающей силы к частоте свободных колебаний системы, а постоянная не зависит от возмущающей силы. Тогда величина амплитуды будет выражаться формулой

Найдем максимум этой функции. Он, очевидно, будет при том значении , при котором квадрат знаменателя имеет минимум. Но минимум функции

(5)

достигается при

и равен

Следовательно, максимальная величина амплитуды равна

Графики функций при различных значениях показаны на рисунке 11 (для определенности при построении графиков положено ). Эти кривые называются кривыми резонанса.

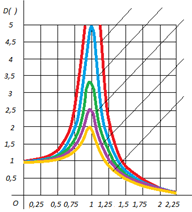
Рис.11

Из формулы (5) следует, что при малых максимальное значение амплитуды достигается при значениях , близких к единице, то есть когда частота внешней силы близка к частоте свободных колебаний. Если (следовательно, ), то есть если отсутствует сопротивление движению, амплитуда вынужденных колебаний неограниченно возрастает при , то есть при :

При имеет место явление резонанса.

2. Предположим теперь, что , то есть рассмотрим уравнение упругих колебаний без сопротивления при наличии периодической внешней силы

(6)

Общее решение однородного уравнения

Если , то есть если частота внешней силы не равна частоте собственных колебаний, то частное решение неоднородного уравнения имеет вид

Подставляя это выражение в исходное уравнение, найдем

Общее решение есть

Таким образом, движение получается в результате наложения собственного колебания с частотой и вынужденного колебания с частотой .

Если , то есть частота собственных колебаний совпадает с частотой внешней силы, то функция (3) не является решением уравнения (6). В этом случае (в соответствии с ЛНДУ II порядка) частное решение надо искать в форме

Подставляя это выражение в уравнение, найдем и :

Следовательно,

Общее решение будет иметь вид

Второй член, стоящей в правой части, показывает, что в этом случае амплитуда колебания неограниченно возрастает при неограниченном возрастании времени t. Это явление, имеющее место при совпадении частоты собственных колебаний системы с частотой внешней силы, называется резонансом.

График функции изображен на рисунке 12.

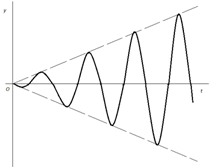
Рис.12