3.5. Теплоотдача при свободной конвекции

Теплообмен при свободном движении жидкости распространен как в технике, так и в быту, в частности, при отоплёнии помещений. Наиболее полно изучено гравитационное свободное движение, возникающее под действием гравитационного поля в системе с неоднородным распределением плотности жидкости. Такое распределение плотности является результатом процесса теплообмена между жидкостью и твёрдым телом (например, между радиатором водяного отоплёния и воздухом).

При свободной конвекции в неограниченном пространстве (в большом объёме) конвективные токи, возникающие у поверхности теплообмена, не вызывают циркуляции основной массы жидкости. Температура жидкости изменяется в пределах теплового пограничного слоя от температуры стенки t_c до температуры жидкости вдали от поверхности t_ж, а скорость w изменяется от нуля у стенки до нуля вдали от неё, проходя через максимум (рис. 3.6).

Рис.3.6. Изменение t_ж, и w при свободном движении среды вдоль нагретой вертикальной стенки.

В случае вертикальной поверхности толщина нагретого слоя вблизи её нижней части мала, и движение жидкости является ламинарным. При подъёме жидкости толщина нагретого слоя увеличивается, и движение становится турбулентным. Характер течения в пограничном слое определяется числом Релея Ra= Gr·Pr.

Значение коэффициента теплоотдачи зависит от толщины пограничного слоя и характера движения жидкости. Изменение α по высоте поверхности показано на рис. 3.7.

Исследования теплообмена жидкостей с телами различной формы в условиях свободного движения в неограниченном пространстве позволили получить уравнения подобия для расчёта средних значений коэффициента теплоотдачи:

для горизонтальных труб

при Radж <500 ,	(3.32)
при 103 < Radж <108 ,	(3.33)

для вертикальных труб и пластин

при ламинарном режиме 10³ < Ra_hж <10⁹

,

(3.34)

при турбулентном режиме Ra_hж >10⁹

,

(3.35)

Для воздуха уравнения (3.33)–(3.35) соответственно примут вид:

, , и

(3.36)

Рис.3.7. Изменение коэффициента теплоотдачи по высоте трубы или пластины при свободном движении среды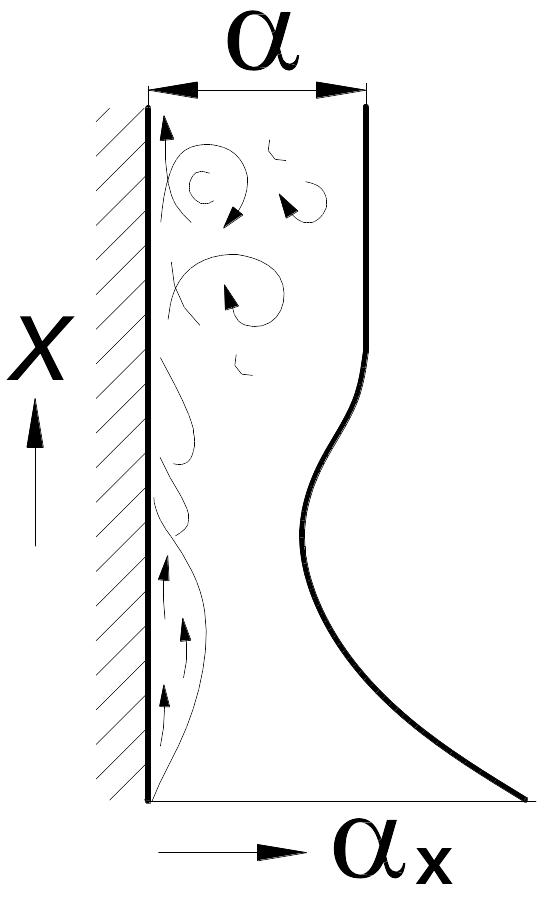

В уравнениях (3.33)–(3.36) в качестве определяющей принята температура жидкости за пределами движущегося слоя, а (3.32) – среднее между значениями температуры жидкости и стенки. В качестве определяющего размера для горизонтальных труб принят диаметр d, а для вертикальных поверхностей – высота h.

Для наклонных поверхностей, образующих угол  с горизонтом, значение коэффициента теплоотдачи рассчитывают по формуле:

(3.37)

Свободная конвекция около горизонтальных пластин зависит от их размеров и положения теплоотдающей поверхности. Если она обращена вниз, то движение жидкости происходит горизонтально в тонком слое под поверхностью, а остальная масса жидкости неподвижна. Если же эта поверхность обращена вверх, то жидкость движется от периферии к центру и там поднимается вверх, а при больших размерах пластины в её центральной части наблюдаются также притоки холодной жидкости сверху.

Для горизонтальных поверхностей коэффициент теплоотдачи рассчитывают по формулам (3.34) либо (3.35), причем в качестве определяющего размера выбирают меньшую из сторон (в плане). Полученное значение α умножают на коэффициент 1,3, если теплоотдающая поверхность обращена вверх, и на 0,7, если она обращена вниз. В том случае, когда температура пластины меньше температуры жидкости, бóльшая интенсивность теплоотдачи будет со стороны нижней поверхности и для расчёта соответствующего значения α надо применять коэффициент 1,3.

В ограниченном пространстве (в узких глухих каналах) нагревание и охлаждение жидкости протекают вблизи друг от друга и образуются восходящие и нисходящие потоки жидкости, зависящие от формы и размеров замкнутого объёма, от рода жидкости и температурного напора. В вертикальных каналах и щелях при большой толщине δ указанные потоки практически не влияют друг на друга и имеют такой же характер, как и в неограниченном пространстве. При малых значениях δ вследствие взаимных помех в щелях возникают внутренние циркуляционные контуры (рис.3.8 а,б).

Рис.3.8. Характер естественной циркуляции жидкости в ограниченном пространстве.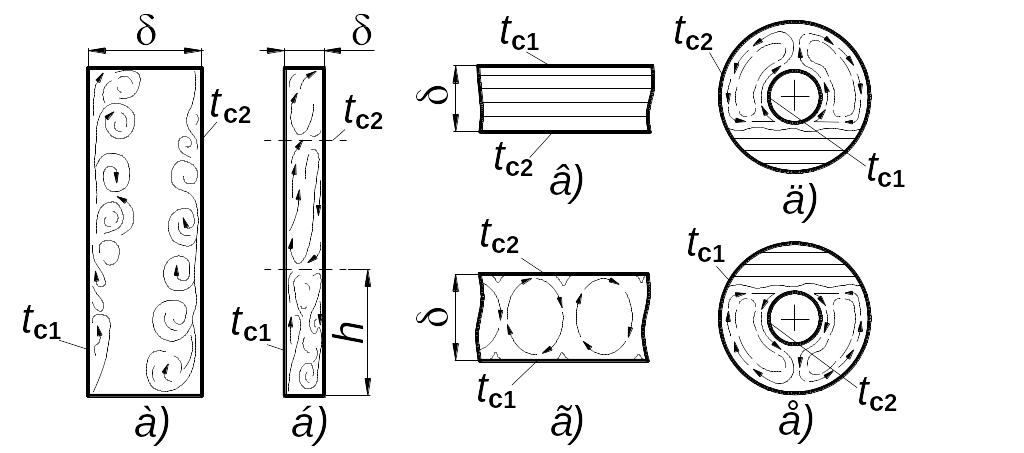

В горизонтальных щелях процесс определяется взаимным расположением нагретых и холодных поверхностей и расстоянием между ними, причем если нагретая поверхность расположена сверху, то циркуляция жидкости не возникает. Расположение нагретой поверхности снизу либо неравномерность температур стенок способствует появлению конвекции (рис.3.8 в, г). В горизонтальных шаровых и цилиндрических прослойках характер циркуляции зависит от их толщины и взаимного положения нагретой и холодной поверхностей. Движение жидкости развивается в зоне, расположенной выше нижней кромки нагретой внутренней поверхности либо ниже верхней кромки холодной внутренней поверхности (рис.3.8 д,е).

Для облегчения расчета сложный процесс переноса теплоты через щели заменяют эквивалентным процессом теплопроводности и вычисляют среднюю плотность теплового потока по формуле:

,

(3.38)

где λ_экв=λ_к – эквивалентный коэффициент теплопроводности,

_к – коэффициент конвекции, учитывающий влияние конвекции на

пере- нос теплоты через щель,

t_c1 и t_c2 – температуры ограждающих поверхностей.

Величина _к является функцией числа Релея. При значениях Ra< 10³ _к =1, то есть передача теплоты через щель осуществляется только теплопроводностью.

При 103<Raδж<106 ,	(3.39)
при 106<Raδж<1010 .	(3.40)

В приближенных расчетах вместо формул (3.39) и (3.40) применяют для всей области 10³<Ra_бж<10¹⁰ единую зависимость:

.

(3.41)

В формулах (3.39) – (3.41) при расчете числа Ra_δж независимо от формы прослойки в качестве определяющего размера принимают её толщину δ, а в качестве определяющей температуры – среднюю температуру жидкости t_ж=0,5(t_с1 +t_с2).

4. ТЕПЛООБМЕН ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО