58

3. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН В ЖИДКОСТЯХ

3.1. Теплоотдача при продольном обтекании пластин

При течении жидкости вдоль плоской поверхности (пластины) образуется динамический пограничный слой, характеризующийся большим градиентом продольной составляющей скорости. В пределах этого слоя под влиянием сил трения скорость изменяется от значения w₀, характерного для всего невозмущенного потока вдали от поверхности, до нуля на поверхности пластины. По мере движения потока толщина слоя возрастает, так как тормозится всё более удалённые струи жидкости. При этом вблизи поверхности течение всегда носит ламинарный характер на любом расстоянии х от передней кромки пластины. Однако с увеличением х и, следовательно, толщины пограничного слоя в нём при определённом значении числа Рейнольдса могут возникать вихри, то есть в значительной части слоя течение становится турбулентным (рис.3.1). Переход к турбулентному режиму происходит при критическом значении числа Re_x, которое обычно полагают равным ≈5·10⁵, причём в качестве определяющего размера принимают расстояние х. По данным некоторых авторов, этот переход может происходить при значениях Re_х.кр от 10⁴ до 4·10⁶.

Рис.3.1. Схема движения жидкости при обтекании пластины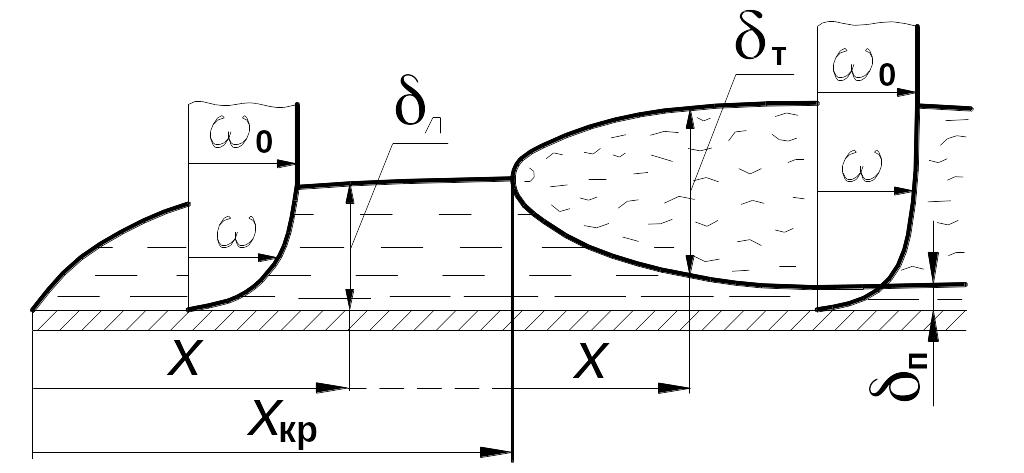

У поверхности пластины образуется также тепловой пограничный слой, в пределах которого изменяется температура жидкости – от температуры невозмущенного потока до температуры стенки. В общем случае толщины динамического  и теплового  пограничных слоёв не совпадают. Соотношение между этими толщинами для ламинарного режима можно определить по формуле

.

(3.1)

При ламинарном режиме течения в пограничном слое для определения среднего коэффициента теплоотдачи используют зависимость

.

(3.2)

При турбулентном режиме справедливо соотношение

.

(3.3)

В формулах (3.2) и (3.3) сомножитель _t=(Pr_р/Pr_с)^0,25, , как отмечено выше (стр. 30), учитывает влияние на теплоотдачу изменения теплофизических свойств жидкости с изменением температуры.

Для воздуха Pr≈0,71, поэтому формулы (3.2) и (3.3) принимают вид

при ,	(3.4)
при .	(3.5)

Формулы (3.1)–(3.5), строго говоря, применимы для условий, когда температура пластины постоянна. При переменной температуре значение Pr_с надо выбирать по средней температуре стенки. Эти формулы можно использовать также для расчёта коэффициента теплоотдачи при внешнем продольном обтекании цилиндра, диаметр которого существенно превышает толщину пограничного слоя.

3.2. Обтекание шара

Средний по поверхности коэффициент теплоотдачи от шара, обтекаемого потоком теплоносителя, можно рассчитать из соотношения

.

(3.6)

В качестве определяющего размера принимают диаметр шара, а все параметры, входящие в числа подобия, соответствуют условиям набегающего потока. Пределы применимости этого уравнения: 0,3Re3^.10⁵ и 0,6Pr8^.10³.

Число Nu при движении газа через плотный слой шаров либо частиц произвольной формы может быть рассчитано по формулам:

при,	(3.7)
при, .	(3.8)

В этих формулах в качестве определяющего размера принимают диаметр шара (если частицы не сферические, то , где V – объём частицы). Определяющая температура t_ж – средняя между температурами газа на входе в слой и на выходе из него. Скорость газа рассчитывается по полному сечению без учёта загромождения сечения частицами.

3.3 Теплоотдача при течении жидкости внутри труб

При течении жидкости в трубах процесс теплоотдачи протекает сложнее, чем при обтекании пластин. На жидкость, текущую вдали от пластины, не влияют процессы, проходящие у стенки, а в трубе, начиная с некоторого расстояния от входа, вследствие конечного размера диаметра весь объём жидкости тормозится силами вязкости, что сказывается на теплоотдаче.

Вынужденное движение жидкости в трубах может быть ламинарным либо турбулентным. Режим течения зависит от числа Рейнольдса: при Re_dж<2^.10³ течение является ламинарным, при Re_dж>10⁴ – развитым турбулентным, а диапазон Re_dж от 2^.10³ до 10⁴ соответствует переходному режиму.

Для ламинарного режима характерно параболическое распределение скоростей по сечению, а для развитого турбулентного режима это распределение имеет вид усеченной параболы. Стабилизация поля скоростей наступает на некотором расстоянии от входа в трубу, при этом у самой поверхности в тонком динамическом пограничном слое течение остаётся ламинарным.

На интенсивность теплоотдачи влияет зависимость теплофизических свойств жидкости от температуры, в частности, изменение вязкости приводит к изменению профиля поля скоростей. На практике скорость и температура на входе в трубу имеют профили, близкие к равномерным. Для этих условий средний коэффициент теплоотдачи при ламинарном режиме течения можно рассчитать по формуле

,

(3.9)

где d и l– диаметр и длина трубы.

В качестве определяющей температуры в уравнении (3.9) принимают среднюю температуру жидкости. Уравнение справедливо при значениях (l/d)>10, Re_dж>10 и 0,06<Pr_ж/Pr_с<10. Оно применимо также для плоских каналов шириной h, при этом вместо диаметра d в уравнение подставляют значение h.

Для труб весьма большой длины, определяемой условием

,

(3.10)

вместо соотношения (3.9) для определения среднего коэффициента теплоотдачи можно использовать приближенную формулу

.

(3.11)

Все приведенные выше соотношения относятся к условия, когда влияние подъёмных сил не проявляется.

Некоторые авторы рекомендуют использовать для определения среднего коэффициента теплоотдачи при вязкостном течении уравнение, предложенное Б.С. Петуховым

,

(3.12)

где Pe=Re∙Pr=wd/a – число Пекле,

_l – поправка на гидродинамический начальный участок

.

(3.13)

Формула (3.12) справедлива при значениях числа Релея Ra=Gr^.Pr= =gtd³/(a)<8^.10⁵, а формула (3.13) – при (1/Re)·(1/d)<0,1.

Существование различных уравнений подобия для расчета среднего коэффициента теплоотдачи для одних и тех же процессов конвективного теплообмена обусловлено эмпирическим характером этих уравнений.

При турбулентном режиме течения перенос теплоты в жидкости осуществляется в основном благодаря её интенсивному перемешиванию. Температура жидкости в ядре потока практически постоянна, а её резкое изменение наблюдается лишь в тепловом приграничном слое.

Ещё в начале ХХ века Нуссельт впервые подробно исследовал теплоотдачу при турбулентном режиме течения газов и применил теорию подобия при обработке опытных данных. В настоящее время для расчёта среднего значения коэффициента теплоотдачи на участке стабилизированного турбулентного течения используют зависимость, предложенную М.А. Михеевым

,

(3.14)

Эта формула справедлива при значениях Re =10⁴÷10⁶ и Pr=0,6÷2500. Определяющим размером является внутренний диаметр трубы, а для канала произвольного сечения, включая кольцевое сечение при d₂/d₁<5, –– эквивалентный диаметр. Определяющей температурой t_ж является средняя температура теплоносителя на входе и выходе трубы.

Значение поправочного коэффициента _l, учитывающего влияние начального участка трубы, где коэффициент теплоотдачи выше, определяется по таблице 3.1. Для достаточно длинных труб (l/d50) _l =1.

Таблица 3.1

Значения поправочного коэффициента _l при турбулентном режиме

Redж	Значения
	1	2	5	10	15	20	30	40	50
	1,65	1,50	1,34	1,23	1,17	1,13	1,07	1,03	1
	1,51	1,40	1,27	1,18	1,13	1,10	1,05	1,02	1
	1,34	1,27	1,18	1,13	1,10	1,08	1,04	1,02	1
	1,28	1,22	1,15	1,10	1,08	1,06	1,03	1,02	1
	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Из формул (3.14) и (3.9) следует, что при турбулентном режиме течения коэффициент теплоотдачи существеннее зависит от скорости потока, чем при ламинарном (пропорционально w^0,8 и w^0,4 соответственно).

Для воздуха и двухатомных газов Pr≈0,71 и Pr_ж/Pr_с≈1, поэтому соотношение (3.14) принимает вид

,

(3.15)

При движении жидкости в изогнутых трубах возникает центробежный эффект, вызывающий в поперечном сечении вторичную циркуляцию, которая увеличивает турбулентность потока и среднее значение . Поэтому для таких труб в формулу (3.14) вводят поправочный множитель _R, равный

,

(3.16)

где R– радиус изгиба.