Работа 6. Термодинамическая оценка процессов выщелачивания, сопровождающихся химическим взаимодействием

Цель – установить концентрационную константу равновесия, определить с использованием коэффициентов активностей термодинамическую константу, вычислить изменение свободной энергии Гиббса и оценить термодинамическую возможность или невозможность реализации конкретного процесса выщелачивания.

Общие сведения. Выщелачивание - это процесс избирательного извлечения ценного компонента в водный раствор.

Выщелачивание – процесс гетерогенный, в котором участвуют, по меньшей мере, две фазы – твердое вещество и раствор. В зависимости от характера физико-химических процессов различают два вида выщелачивания: простое выщелачивание и выщелачивание с химической реакцией.

Простое выщелачивание не сопровождается химическим взаимодействием и характеризуется тем, что элемент извлекается в раствор в форме соединения, в составе которого находятся в исходном сырье (сильвин – KCl, каменная соль – NaCl и др.). Поэтому простому растворению предшествуют подготовительные операции трансформации металла в растворимую форму – спекание, сплавление, сульфатизирующий или хлорирующий обжиг и др.

В простом растворении участвуют вещества, в твердом состоянии образующие ионную кристаллическую решетку, а в растворе они присутствуют в виде гидратированных ионов. Соответственно, изменение энергии Гиббса при растворении определяется энергией кристаллической решетки и энергией гидратации ионов

. (1)

При выщелачивании с химической реакцией металл, присутствующий в исходном сырье в виде мало растворимого в воде соединения, переводится под действием реагента в растворимую форму. Выщелачивание с химическим взаимодействием наиболее распространенный вид выщелачивания, часто требующий предварительной подготовки природного. При выщелачивании могут протекать реакции между оксидами и кислотами или щелочами, обменные или окислительно-восстановительные реакции.

Термодинамическое исследование физико-химических превращений заключается в изучении и сравнении термодинамических характеристик начального (исходного) и конечного (равновесного) состояния системы. Наиболее важными термодинамическими характеристиками физико-химических процессов являются изменения энергии Гиббса и изменение энтропии.

Изменение энергии Гиббса характеризует равновесное состояние системы и возможность самопроизвольного протекания изучаемого процесса при определенной температуре и давлении. До начала превращения энергия Гиббса (ΔG_нач) представляет собой функцию исходного состояния систем при начальной температуре:

ΔG_нач = RT ln П(a_i^±υi )+ ΔG_i⁰_, (2)

где a_i – активность реагирующих веществ и продуктов реакции до начала процесса; υ_i – стехиометрические коэффициенты в уравнении химической реакции, для исходных веществ берутся со знаком (–), а для продуктов реакции - со знаком (+); ΔG_i⁰ – стандартная энергия Гиббса.

Энергия Гиббса системы после протекания реакции и установления равновесия (G_р) представляет собой функция равновесного состава системы и является постоянной величиной для заданной температуры, характерной для каждой химической реакции:

ΔG_p = RT ln Π(a_i^±υi )_равн + ΔG_i⁰ = RT ln K_p + ΔG_i⁰, (3)

где Π(a_i^±υi )_равн = K_p;

K_p – константа равновесия, характерная для исследуемого процесса, является величиной постоянной.

Изменение энергии Гиббса в результате осуществления взаимодействия определяется разностью уравнений (2) и (3):

ΔG_p = ΔG_нач + ΔG_равн = RT[ln П(a_i^±υi ) – ln K_p]. (4)

Когда процесс осуществляется в стандартных условиях (Т = 298К, а_i = 1), то ln П(a_i^±υi ) = 0, и уравнение (4) имеет вид:

ΔG⁰₂₉₈ = –RT lnK_p. (5)

Известно, что энтальпия системы характеризует тепловой эффект реакции, а также зависимость константы равновесия реакции от температуры:

ΔH = ΔH_нач – ΔH_равн . (6)

Значение энтальпии для начального и конечного (равновесного) состояния системы, имеет постоянную величину при заданных условиях, характерную для каждого физико-химического превращения.

Зависимость константы равновесия реакции от температуры выражает уравнение изобары Вант-Гоффа:

(7)

Энергия Гиббса и энтальпия физико-химического превращения при заданной температуре связаны между собой уравнением Гиббса-Гельмгольца:

(8)

Как видно из уравнения, выделение тепловой энергии в ходе взаимодействия способствует самопроизвольному протеканию процесса, что соответствует отрицательному значению энтальпии. К аналогичному явлению приводит рост энтропии системы. Однако известно, что величины энтальпии и энтропии могут иметь как отрицательные, так и положительные значения, поэтому предвидеть заранее направление протекания процесса затруднительно.

При низких температурах изменением энтропии при протекании реакции можно пренебречь, тогда энергия Гиббса и энтальпия процесса пропорциональны друг другу:

ΔG_Р = ΔH + const (9)

Это соотношение иногда используют для приближенной оценки изменения энергии Гиббса по тепловому эффекту реакции.

При высоких температурах (особенно в расплавленных средах) доля (ТΔS) в величине энергии Гиббса превалирует и определяет ее зависимость от температуры.

По уравнению (8) можно рассчитать величину константы равновесия реакции по стандартным значениям энтальпии и энтропии:

(10)

Термодинамическая константа равновесия ( ) для заданной температуры может быть рассчитана с использованием уравнений (5) и (8) по стандартному изменению энергии Гиббса, энтальпии и энтропии веществ, участвующих в реакции, которые приводятся в справочной литературе.

Константу равновесия реакции можно также определить экспериментально. Однако прямой эксперимент позволяет определить концентрационную константу равновесия

. (11)

Последняя зависит от состава и ионной силы раствора:

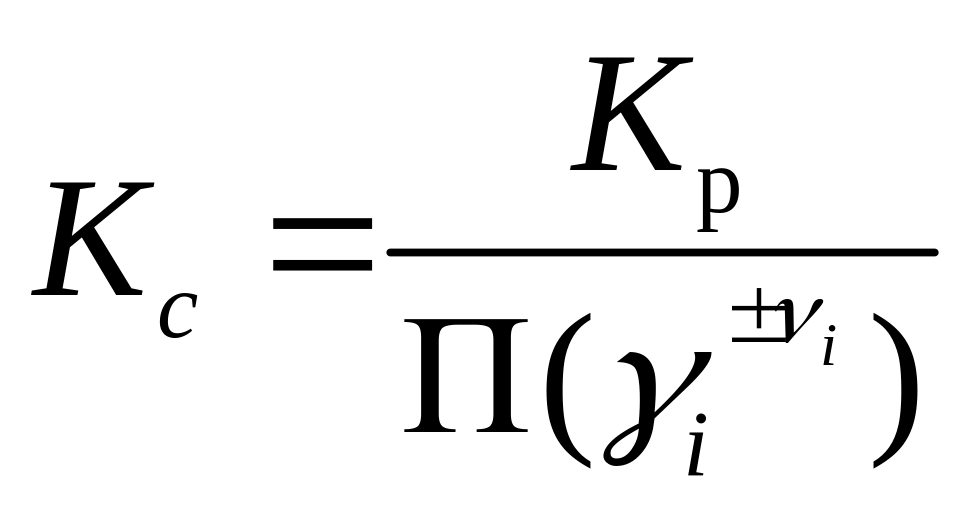, (12)

где: _ - коэффициенты активности реагирующих веществ и продуктов реакции до начала процесса; .

С

овпадение величин К_р и К_с достигается в условиях, когда . Исходя из этого, определение термодинамической константы равновесия возможно осуществить путем графической экстраполяции величины К_с к бесконечному разведению раствора (рис.1).

К

Рис. 1. Графический метод определения К_р по зависимости К_с от концентрации (ионной силы) раствора.

онцентрационная константа равновесия имеет самостоятельное значение для расчетов расхода реагента при извлечении металла в раствор. Например, при растворении оксидов металлов кислотами, процесс описывается в общем виде следующими уравнениями:

а) для двухосновной кислоты и двухвалентного металла:

МеО_(т) + Н₂А_(р) = МеА_(р) + Н₂О, (13)

где А – анион кислоты.

Константа равновесия этой реакции:

. (14)

После достижения равновесия, когда металл практически растворится, в растворе должен остаться избыток растворителя (кислоты):

(15)

или (16)

где n_i – число молей вещества.

Кроме этого, для растворения оксида металла в соответствии с уравнением реакции (13) необходим 1 моль кислоты на 1 моль оксида. Таким образом, для полного растворения оксида металла необходимо взять кислоты в количестве на менее, чем

, . (17)

Минимальная исходная концентрация кислоты в растворе составит:

, (18)

где V – объем раствора.

б) для одноосновной кислоты и двухвалентного металла уравнение реакции имеет вид:

МеО_(т) + 2НА_(р) = МеА_2(р) + Н₂О, (19)

Константа равновесия этой реакции:

. (20)

Избыточное количество кислоты в конце реакции:

(21)

или

(22)

Кроме того, для растворения оксида металла в соответствии с уравнением реакции (19) необходимо иметь 2 моля кислоты на 1 моль оксида. Таким образом, для полного растворения оксида необходимо использовать кислоту в количестве не менее, чем

, . (23)

Исходная концентрация кислоты в растворе должна быть не менее, чем:

(24)

Д

Рис.2. Графическое определение К_с

1 – прямая реакция, 2 – обратная реакция

ля экспериментального определения К_с нужно взять некоторое количество исходных веществ (оксида и кислоты) и фиксировать изменение во времени концентрации исходных веществ и продуктов реакции вплоть до установления равновесия при постоянной температуре.

Величину К_с определяют графической экстраполяцией (рис.2) при отношений или .

Порядок выполнения работы. Лабораторная установка включает: стакан с растворителем - 1; перемешивающее тело (магнитик) - 2; магнитную мешалку с подогревающим устройством - 3;

термометр - 4.

Необходимая посуда, материалы и реагенты: стеклянный стакан на 500 мл; мерный цилиндр на 500 мл; конические колбы на 250 мл; пипетки на 5 мл; оксид меди (порошок); раствор муравьиной кислоты (CH₂O₂) концентрацией 90 %; раствор уксусной кислоты (CH₃COOH) концентрацией 99,5 %; раствор соляной кислоты концентрацией 2 N; раствор тиосульфата натрия (Na₂S₂O₃) концентрацией 0,05 N; 20 %-ный раствор иодистого калия; раствор крахмала (индикатор).

Все опыты проводятся при постоянном перемешивании и при постоянной температуре.

1. Приготовить 300 мл раствора заданного состава и концентрации (табл.1), который затем слить в стеклянный стакан емкостью 500 мл.

Таблица 1