
- •Теория металлургических процессов
- •Введение
- •Работа 1. Исследование реакции газификации углерода
- •Работа 2. Исследование процесса прямого восстановленя оксида железа
- •Работа 3. Исследование химичекой кинетики реакций диссоциации карбонатов
- •Работа 4. Исследование кинетики окислительного обжига сульфидного цинкового концентрата
- •Работа 5. Изучение реакций в системе Ме-s-о
- •Работа 6. Термодинамическая оценка процессов выщелачивания, сопровождающихся химическим взаимодействием
- •Варианты работы и условия опыта
- •Результаты анализа раствора
- •Работа 7. Исследование влияния пассивации поверхности минералов на процесс выщелачивания
- •Работа 8. Очистка раствора сульфата цинка от меди методом цементации
- •Приложение Определение концентрации меди.
- •Оглавление
Работа 3. Исследование химичекой кинетики реакций диссоциации карбонатов
Цель – определить энергию активации реакции диссоциации карбоната.
Общие сведения. При заданных внешних условиях (температура, давление, среда, в которой происходит процесс) скорость химического превращения является функцией только концентраций компонентов реакционной смеси. Уравнение, описывающее зависимость скорости химического процесса от концентрации компонентов реакционной смеси, называется кинетическим уравнением химического процесса.
Очень часто в химической кинетике приходится иметь дело с процессами, скорость которых оказывается пропорциональной произведению концентраций реагирующих веществ в соответствующих степенях.
Если зависимость скорости реакции от концентрации реагирующих веществ записывается в виде
= k [А1]n1 [А2]n2…[Аi]ni (1)
то величины n (i = 1, 2, …) принято называть порядком реакции по веществу Ai. Сумму порядков реакции по всем реагирующим веществам называют порядком реакции.
Множитель k в кинетическом уравнении (1), показывающий, с какой скоростью идет химический процесс при концентрациях реагирующих веществ, равных единице, называется константой скорости химического процесса.
Наряду со скоростью константа скорости химического процесса является основной величиной в химической кинетике.
Cтепенная зависимость скорости реакции от концентраций реагирующих частиц (1) практически всегда выполняется для скорости отдельных стадий химического процесса. При этом
как порядок по отдельному компоненту, так и суммарный порядок реакции являются целыми положительными числами. Для отдельной стадии порядок реакции никогда не превышает трех. Поэтому особо важное значение в химической кинетике имеют реакции первого, второго и третьего порядка.
Константы скорости реакций различного порядка имеют различную размерность. Поскольку размерность скорости реакции, независимо от кинетического уравнения этой реакции, есть [с][t]-1, то из (1) следует, что размерность константы скорости для реакции первого порядка [t]-1, второго порядка [с]-1[t]-1, третьего порядка [с]-2[t]-1.
Концентрации в химической кинетике принято измерять либо числом частиц в 1 cм3 (молекула/см3 или просто см-1), либо в молях в литре (моль/л или М). Соответственно этому, если в качестве единиц для измерения времени принята секунда, для измерения констант скорости могут применяться следующие единицы:
константа скорости первого порядка: сек-1;
константа скорости втopoгo порядка: см3 /молекуласек или см3сек-1 и л/мольсек. или М-1с-1;
константа скорости третьего порядка: см6/молекула2сек или см6сек-1 и л2/ моль2сек или М-2сек-1.
Иногда в качестве единиц измерения времени вместо секунд применяют минуты или часы.
Константа скорости химической реакции, как правило, резко растет с ростом температуры. Зависимость константы скорости реакции от температуры в большом числе случаев может быть описана уравнением Аррениуса
k = k0 e -E/RT (2)
где Т – абсолютная температура, К; k0 и Е — постоянные параметры.
Поскольку концентрация реагирующих веществ практически не зависит от температуры, то такое же соотношение получается и для скорости процесса
= 0 e -E/RT (3)
где 0 = k0 [А1]n1 [А2]n2…[Аi]ni
Относительное увеличение скорости реакции с температурой характеризуется логарифмической производной по Т, т. е. величиной
![]() =
=![]() =
=![]() (4)
(4)
Таким образом, чем больше величина Е, тем быстрее растет скорость реакций с температурой. В случае простых реакций параметр Е показывает, какой минимальной энергией (в расчете на 1 моль) должны обладать реагирующие частицы, чтобы они могли вступить в химическую реакцию. Частицы, энергия которых больше или равна называются активными, а параметр Е в связи с этим называют энергией активации.
В случае сложных реакций, состоящих из нескольких стадий, параметр Е в уравнении (2), как правило, не имеет такого простого физического смысла и является некоторой функцией энергий активации отдельных стадий. Тем не менее и в этом случае параметр Е принято называть энергией активации, хотя правильнее называть его эффективной или эмпирической энергией активации.
Параметры Е и k0 могут быть определены из зависимости константы скорости реакции от температуры с помощью уравнения (2), записанного в виде
ln
k = ln k0
–
![]()
Из линейной зависимости ln k от 1/Т методом наименьших квадратов легко находятся параметры ln k0 и E/R, а из них – Е и k0.
В принципе, для определения Е и k0 достаточно знать константы скорости k1 и k2 при двух значениях температуры Т1 и Т2. Согласно (2)
Е
=

Такое определение Е, как правило, не обеспечивает достаточной точности и рекомендуется определение энергии активации проводить не менее чем по четырем значениям константы скорости при четырех различных температурах.
В случае выполнения уравнения Аррениуса зависимость константы скорости от температуры в координатах ln k — 1/Т должна графически изображаться прямой. Энергия активации в этом случае может быть определена графически из тангенса угла наклона прямой по формуле
Е = R | tg | (5)
г
Рис.
1. Зависимость ln
k
от 1/Т
в
реакции распада ССl4
в газовой фазе.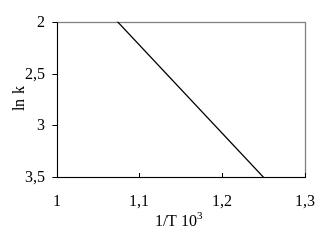
Н
Для сложных реакций уравнение Аррениуса может оказаться неприменимым. Более того, оно оказывается не вполне строгим и для простых реакций, хотя отклонения от него в этом случае удается заметить лишь при очень прецизионных измерениях. Тем не менее и в случае отчетливых отклонений от уравнения Аррениуса нередко пользуются соотношениями (2) и (3) для выражения зависимости константы скорости или скорости реакции от температуры, полагая величины k0 или 0 и Е переменными, т.е. функциями температуры. Функцию Е при этом также называют энергией активации. Эта функция находится с помощью дифференциальной формы уравнения Аррениуса (4)
Е
= RT2![]() =
RT2
=
RT2![]()
дифференцированием найденной из эксперимента зависимости ln k или ln от температуры.
Иногда зависимость скорости реакции от температуры характеризуют величиной температурного коэффициента, который определяют как возрастание скорости при увеличении температуры на 10°
(Т)
=
![]() (6)
(6)
Температурный коэффициент реакции связан с величиной энергии активации соотношением, которое легко получается при подстановке (3) в (6).
(Т)
=
![]()
порядок проведения работы. Установить заданную температуру (Т1) в муфельной печи. Поместить 5 алундовых тиглей с предварительно взвешенными на технических весах навесками MgCO3 по 1 г и выдержать навески в течении 5, 10, 15, 20, 30 мин соответственно. Зафиксировать убыль веса навески ∆m при диссоциации карбоната MgCO3 по реакции:
MgCO3 = MgO + CO2
Эксперимент провести при более высокой температуре Т2.
Обработка полученных данных сводится к следующей последовательности: построить графические зависимости степени диссоциации от времени при температурах Т1 и Т2, определить константы скорости химической реакции (k1 и k2), рассчитать энергию активации Е. По величине Е сделать вывод о режиме протекания процесса.
Таблица.1.
Данные измерений и вычислений
, мин |
Т1, К |
Т2, К |
||
∆m, г |
, % |
∆m, г |
, % |
|
|
|
|
|
|
