3. Методи суб'єктивних вимірів

При формуванні ситуацій, цілей, обмежень і варіантів рішень ЛПР і експерти роблять об'єктивні й суб'єктивні виміри характеристик вірогідності, важливості та переваги. Для здійснення суб'єктивних вимірів застосовуються різні методи, до найбільш уживаних з яких відносяться: ранжирування, парне порівняння, безпосередня оцінка та послідовне порівняння.

При описі кожного з перерахованих методів буде передбачатися, що є кінцеве число вимірюваних об'єктів x = (x₁, …, х_m) і сформульований один або кілька ознак порівняння, по яких здійснюється порівняння властивостей об'єктів. Отже, методи виміру будуть розрізнятися лише процедурою порівняння об'єктів. Ця процедура включає побудову відносин між об'єктами емпіричної системи, вибір функції, що відображає, f і визначення типу шкали вимірів. Розглянемо всі ці питання для кожного методу виміру.

Ранжування являє собою процедуру впорядкування об'єктів, виконувану ЛПР або експертом. На основі знань і досвіду ЛПР або експерт розташовує об'єкт у порядку переваги, керуючись одним або кількома обраними показниками порівняння. Залежно від виду відносин між об'єктами можливі різні варіанти впорядкування об'єктів. Розглянемо ці варіанти. Нехай серед об'єктів немає однакових за порівнюваними показниками, тобто немає еквівалентних об'єктів. У цьому випадку між об'єктами існує тільки відношення строгого порядку. У результаті порівняння всіх об'єктів по відношенню строгого порядку складається впорядкована: послідовність

x₁ ≻ x₂ ≻ x₃ ≻ … ≻ x_m, (1)

де об'єкт із першим номером є найбільш кращим із всіх об'єктів, об'єкт із другим номером менш кращий першому об'єкту, але переважніше всіх інших об'єктів і т.д.

Отримана система об'єктів з відношенням строгого порядку за умови порівнянності всіх об'єктів по цьому відношенню утворить повний строгий порядок. Для цього відношення доведене існування числової системи, елементами якої є дійсні числа, зв'язані між собою відношенням нерівності [89]. Це означає, що впорядкуванню об'єктів (1) відповідає впорядкування чисел

c₁ > c₂ > c₃ > … > c_m, (2)

де c_i = f(x_i). Можлива й зворотна послідовність

c₁ < c₂ < c₃ < … < c_m, (3)

у якій найбільш кращому об'єкту приписується найменше число й у міру убування переваги в (1) об'єктам приписуються більші числа.

Відповідність послідовностей (1) і (2) або (1) і (3), тобто їх ізоморфізм або гомоморфізм, можна здійснити, вибираючи будь-які числові подання. Єдиним обмеженням є монотонність перетворення. Отже, припустиме перетворення при переході від одного числового подання до іншого повинне мати властивість монотонності. Але такою властивістю припустимого перетворення володіє шкала порядків, тому ранжування об'єктів є вимір у порядковій шкалі.

У практиці ранжирування найчастіше застосовується числове подання послідовності (1) у вигляді натуральних чисел

c₁ = f(x₁) = 1, c₂ = f(x₂) = 2, …, c_m = f(x_m) = m, (4)

тобто використовується числова послідовність типу (3). Числа c₁, з₂,…, c_mу цьому випадку називаються рангами й звичайно позначаються буквами r₁, r₂, …, r_m...

Нехай тепер, крім відносин строгого порядку, між об'єктами є відношення еквівалентності. Упорядкування об'єктів у цьому випадку може мати, наприклад, наступний вигляд:

x₁ ≻ x₂ ≻ x₃ ∾ x₄ ∾ x₅ ≻ x₆ ≻ … ≻ x_m-1 ∾ x_m (5)

У цьому впорядкуванні еквівалентні між собою об'єкти x₃, х₄, x₅ і x_m-1, x_m. Упорядкування (5) утворює нестрогий порядок. Для відношення нестрогого порядку доведене існування числової системи з відносинами нерівності й рівності між числами, що описують властивості об'єктів. Будь-які дві числові системи для нестрогого порядку пов'язані між собою монотонними перетвореннями. Отже, ранжування за умови наявності еквівалентних об'єктів являє собою вимір у порядковій шкалі [93].

У практиці ранжирування об'єктів, між якими допускаються як відносини строгого порядку, так і еквівалентності, числове подання вибирається в такий спосіб. Найбільш кращому об'єкту привласнюється ранг, дорівнює одиниці, другому по перевазі - ранг, рівний двом, і т.д. Для еквівалентних об'єктів зручно з погляду технології наступної обробки експертних оцінок призначити однакові ранги, рівні середньому арифметичному значенню рангів, що привласнюються однаковим об'єктам. Такі ранги називають зв'язаними рангами. Для приклада впорядкування (5) при m = 10 ранги об'єктів x₃, x₄, x₅ будуть рівними: r₃ = r₄ = r₅ = (3+4+5)/3 = 4. У цьому ж прикладі ранги об'єктів x₉, х₁₀ також однакові й. рівні середньому арифметичному r₉ = r₁₀ = (9+10)/2 = 9,5. Як треба із цього приклада, зв'язані ранги можуть виявитися дробовими числами.

Зручність використання зв'язаних рангів полягає в тому, що сума рангів m об'єктів дорівнює сумі натуральних чисел від одиниці до m. При цьому будь-які комбінації зв'язаних рангів не змінюють цю суму. Ця обставина істотно спрощує обробку результатів ранжирування при груповій експертній оцінці.

При груповому ранжируванні кожний s-й експерт привласнює кожному i-му об'єкту ранг r_is У результаті проведення експертизи виходить матриця рангів ||r_is|| розмірності md, де d — число експертів, m — число об'єктів (s = 1, 2, …, d; i= 1, 2, …, m)... Зручно представити результати групового експертного ранжирування у вигляді табл. 3.2.

ТАБЛИЦЯ 3.2

Експерти Об'єкти	э1	э2	…	эd
x1	r11	r12	…	r1d
x2	r21	r22	…	r22
…	…	…	…	…
xm	rm1	rm2	…	rmd

Аналогічний вид має таблиця, якщо здійснюється ранжирування об'єктів одним ЛПР (або експертом) по кількох показниках порівняння. Як приклад наведена табл. 3.3, у якій дані результати ранжирування об'єктів по показниках a_j

ТАБЛИЦА 3.3

Показники Об'єкти	a1	a2	…	aq
x1	r11	r12	…	r1q
x2	r21	r22	…	r2q
…	…	…	…	…
xm	rm1	rm2	…	rmq

Нагадаємо, що ранги об'єктів визначають тільки порядок розташування об'єктів по показниках порівняння. Ранги як числа не дають можливості зробити висновок про те, на скільки або в скільки разів переважніше один об'єкт у порівнянні з іншим. Якщо, наприклад, ранг об'єкта дорівнює трьом, то звідси не слід робити висновок про те, що об'єкт, що має ранг, дорівнює одиниці, у три рази переважніше, ніж об'єкт, що має ранг, рівний трьом.

Достоїнством ранжирування як методу суб'єктивного виміру є простота здійснення процедур, не потребуючого якого-небудь трудомісткого навчання експертів. Недоліком ранжирування є практична неможливість упорядкування великої кількості об'єктів. Як показує досвід, при числі об'єктів, більшому 15-20, експерти затрудняються в побудові ранжирування. Це пояснюється тим, що в процесі ранжирування експерт повинен установити взаємозв'язок між всіма об'єктами, розглядаючи їх як єдину сукупність. При збільшенні числа об'єктів кількість зв'язків між ними росте пропорційно квадрату числа об'єктів. Збереження в пам'яті та аналіз великої сукупності взаємозв'язків між об'єктами обмежуються психологічними можливостями людини. Тому при ранжируванні великої кількості об'єктів експерти можуть припускатись істотні помилки.

Подання (6) є характеристичною функцією відносин нестрогого порядку. Результати порівняння всіх пар об'єктів зручно представляти у вигляді матриці. Нехай, наприклад, є 5 об'єктів х₁, …, x₅ і проведене парне порівняння цих об'єктів по перевазі. Результати порівняння представлені у вигляді x₁ ≻ x₂, x₁ ≻ x₃, x₁ ≻ x₄, x₁ ≺ x₅, x₂ ≻ x₃, x₂ ≻ x₄, x₂ ≺ x₅, x₃ ∾ x₄, x₃ ≺ x₅, x₄ ≺ x₅. Використовуючи числове подання (6), складемо матрицю виміру результатів парних порівнянь (табл. 3.4).

ТАБЛИЦЯ 3.4

	x1	x2	x3	x4	x5
x1	1	1	1	1	0
x2	0	1	1	1	0
x3	0	0	1	1	0
x4	0	0	1	1	0
x5	1	1	1	1	1

Парне порівняння являє собою процедуру встановлення переваги об'єктів при порівнянні всіх можливих пар. На відміну від ранжирування, в якому здійснюється впорядкування всіх об'єктів, парне порівняння об'єктів являє собою більш просте завдання. При порівнянні пари об'єктів можливо або відношення строгого порядку, або відношення еквівалентності. Звідси слідує, що парне порівняння, так само як і ранжирування, є вимір у порядковій шкалі.

У результаті порівняння пари об'єктів x_i, x_j експерт упорядковує її, висловлюючи або x_i ≻ x_j, або x_i ≺ x_j, або x_i ∾ x_j, вибір числового подання f(x_i) можна зробити так: якщо x_i ≻ x_j, те f(x_i) > f(x_j); якщо перевага в парі зворотна, то знак нерівності заміняється на зворотний, тобто f(x_i) < f(x_j). Нарешті, якщо об'єкти еквівалентні, то природно вважати, що f(x_i) = f(x_j).

У практиці парного порівняння використовуються наступні числові подання:

або

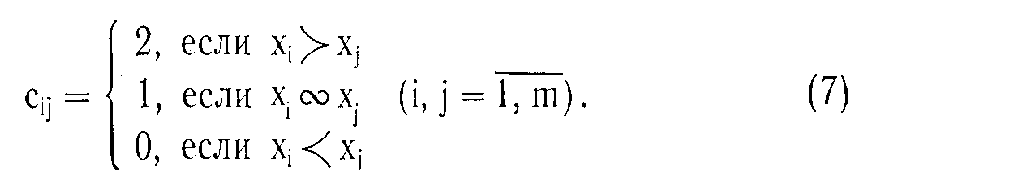
У табл. 3.4 на діагоналі завжди будуть розташовані одиниці, оскільки об'єкт еквівалентний собі.

Подання (7) характерно для відображення результатів спортивних змагань. За виграш дається два очка, за нічию – одне, за програш - нуль очків (футбол, хокей і т.п.). Перевага одного об'єкта перед іншим трактується в цьому випадку як виграш одного учасника турніру у іншого. Таблиця результатів виміру при використанні числового подання не відрізняється від таблиць результатів спортивних турнірів, за винятком діагональних елементів (звичайно в турнірних таблицях діагональні елементи заштриховані). Як приклад у табл. 3.5 наведені результати виміру п'яти об'єктів з використанням подання (7), що відповідають табл. 3.4

ТАБЛИЦЯ 3.5

	x1	x2	x3	x4	x5
x1	1	2	2	2	0
x2	0	1	2	2	0
x3	0	0	1	1	0
x4	0	0	1	1	0
x5	2	2	2	2	1

Якщо порівняння пар об'єктів проводиться окремо за різними показниками або порівняння здійснює група експертів, то по кожному показнику або експертові складається своя таблиця результатів парних порівнянь. Тому утворюється пакет таблиць. Порівняння у всіх можливих парах не дає повного впорядкування об'єктів. Тому виникає завдання ранжирування об'єктів за результатами їхнього парного порівняння. Рішення цього завдання можливо за певних умов і буде розглянуто далі в гл. 6. Помітимо, що результати ранжирування завжди можна надати у вигляді матриці парних порівнянь. Таке подання зручно для проведення обробки результатів групового ранжирування.

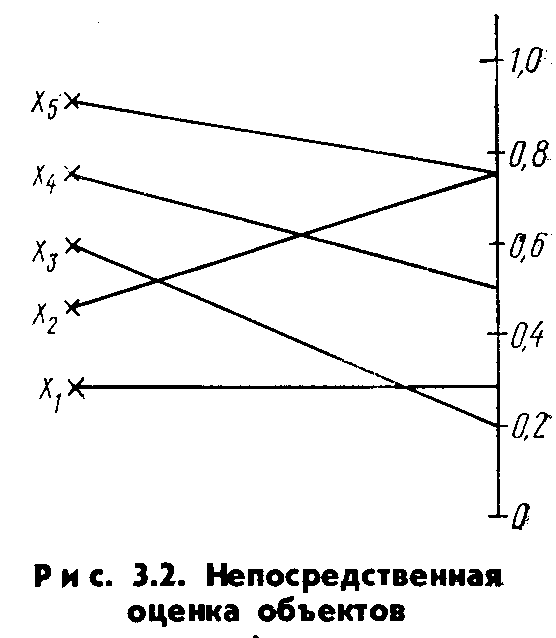
Безпосередня оцінка являє собою процедуру приписування об'єктам числових значень у шкалі інтервалів. ЛПР або експертові необхідно поставити у відповідність кожному об'єкту крапку на певному відрізку числової осі. Природно вимагати, щоб еквівалентним об'єктам приписувалися однакові числа. Зручно результат приписування об'єктам чисел представити графічно. На мал. 3.2 як приклад наведене таке подання для п'яти об'єктів на відрізок числової осі [0, 1]. Оскільки за початок відліку обрана нульова крапка, то в даному прикладі вимір виробляється в шкалі відносин. ЛПР або експерт з'єднує кожний об'єкт лінією із крапкою числової осі. З малюнка видно, що числові подання об'єктів рівні: f(x₁) = 0,28; f(x₂) = f(x₅) = 0,75; f(x₃) = 0,2; f(x₄) = 0,5.

Виміри в шкалі інтервалів можуть бути здійснені з достатньою точністю при повній інформованості ЛПР (експертів) про властивості об'єктів. Ці умови на практиці зустрічаються рідко, тому для виміру застосовують бальну оцінку. При цьому замість безперервного відрізка числової осі розглядають ділянки, кожному з яких приписується свій бал. ЛПР або експерт, приписуючи об'єкту бал, тим самим вимірює його з точністю до певного відрізка числової осі. Застосовуються 5-, 10- і 100-бальні шкали.

Послідовне порівняння являє собою комплексну процедуру виміру, що включає як ранжирування, так і безпосередню оцінку [101]. При послідовному порівнянні ЛПР (експерт) виконує наступні операції:

а) здійснює ранжирування об'єктів;

6) робить безпосередню оцінку об'єктів на відрізку [0, 1], вважаючи, що числова оцінка першого в ранжируванні об'єкта дорівнює одиниці, тобто f(x₁) = 1;

в) вирішує, чи буде перший об'єкт перевершувати по перевазі всі інші об'єкти разом узяті. Якщо так, то експерт збільшує значення числової оцінки першого об'єкта так, щоб вона стала більше суми числових оцінок інших об'єктів, тобто f(x₁) >  f(x_i). У противному випадку він змінює величину f(x₁) так, щоб вона стала менше, ніж сума оцінок інших об'єктів;

г) вирішує, чи буде другий об'єкт переважніше, ніж всі наступні разом узяті об'єкти й змінює f(x₂)так само, як це описано для f(x₁) у пункті в);

д) продовжує операцію порівняння переваги наступних об'єктів і змінює числові оцінки цих об'єктів залежно від свого рішення про перевагу.

Крім описаної процедури послідовного порівняння, існують кілька її модифікацій [101], які незначно відрізняються від розглянутої вище. Метод послідовного порівняння успішно застосовувався для рішення ряду завдань прийняття рішень [108, 114].

Розглянуті чотири методи виміру - ранжирування, парне порівняння, безпосередня оцінка й послідовне порівняння - мають різні якості, але приводять до близьких результатів. Експериментальна порівняльна оцінка цих методів показала, що найбільш ефективним є комплексне застосування всіх методів для рішення однієї й того ж завдання [105]. При цьому варто враховувати, що методом, що вимагає мінімальних трудовитрат, є ранжирування, а найбільш трудомістким - метод послідовного порівняння. Метод парного порівняння без додаткової обробки не дає повного впорядкування об'єктів.