
Вариант 1
Задача
1. Написать
разложение вектора
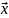 по векторам, если
по векторам, если
 ,
,
 ,
,
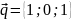 ,
,
 .
.
Задача
2. Коллинеарны
ли векторы
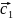 и
и
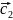 ,
построенные по векторам
,
построенные по векторам
 и
и
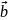 ?
?
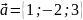 ,
,
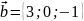 ,
,
 ,
,
 .
.
Задача
3. Найти
косинус угла между векторами
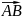 и
и
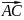 ,
если
,
если
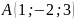 ,
,
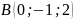 ,
,
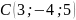 .
.
Задача
4. Компланарны
ли векторы
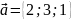 ,
,
 ,
,
 ?
?
Задача
5. Дана прямая
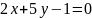 .
Оставить уравнение прямой, проходящей
через точку
.
Оставить уравнение прямой, проходящей
через точку
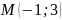 :
а) параллельно данной прямой; б)
перпендикулярно данной прямой.
:
а) параллельно данной прямой; б)
перпендикулярно данной прямой.
Задача 6. Даны
уравнения двух сторон ромба
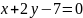 и
и
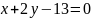 и
уравнение его диагонали
и
уравнение его диагонали
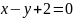 .
Найти координаты вершин ромба и вычислить
его площадь.
.
Найти координаты вершин ромба и вычислить
его площадь.
Задача 14. Построить
линию
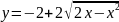 .
.
Задача 15. Составить
уравнение линии, для каждой точки которой
ее расстояние до точки
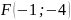 равно расстоянию до прямой
равно расстоянию до прямой
 .
Сделать чертеж.
.
Сделать чертеж.
Вариант 2
Задача
1. Написать
разложение вектора
по векторам, если
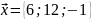 ,
,
 ,
,
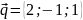 ,
,
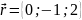 .
.
Задача
2. Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
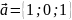 ,
,
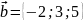 ,
,
 ,
,
 .
.
Задача
3. Найти
косинус угла между векторами
и
,
если
 ,
,
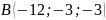 ,
,
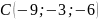 .
.
Задача
4. Компланарны
ли векторы
 ,
,
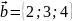 ,
,
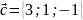 ?
?
Задача
5. Через
вершины треугольника
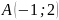 ,
,
 ,
,
 проведены прямые параллельно противолежащим
сторонам. Составить их уравнения.
проведены прямые параллельно противолежащим
сторонам. Составить их уравнения.
Задача
6. В
параллелограмме известны уравнения
двух сторон
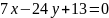 и
и
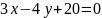 и
точка пересечения диагоналей
и
точка пересечения диагоналей
 .
Определить длины высот параллелограмма.
.
Определить длины высот параллелограмма.
Задача 14. Построить
линию
 .
.
Задача 15. Составить
уравнение линии, для каждой точки которой
отношение расстояний до точки
 и прямой
и прямой
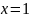 равно
равно
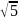 .
Сделать чертеж.
.
Сделать чертеж.
Вариант 3
Задача
1. Написать
разложение вектора
по векторам, если
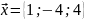 ,
,
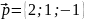 ,
,
 ,
,
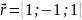 .
.
Задача
2. Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
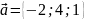 ,
,
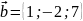 ,
,
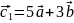 ,
,
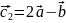 .
.
Задача
3. Найти
косинус угла между векторами
и
,
если
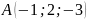 ,
,
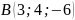 ,
,
 .
.
Задача
4. Компланарны
ли векторы
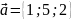 ,
,
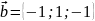 ,
,
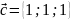 ?
?
Задача
5. Две стороны
квадрата лежат на прямых
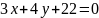 ,
,
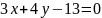 .
.
Вычислить площадь квадрата.
Задача
6. Даны
уравнения двух высот треугольника
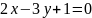 и
и
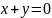 и
координаты одной из его вершин
и
координаты одной из его вершин
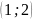 .
Составить уравнения сторон треугольника.
.
Составить уравнения сторон треугольника.
Задача 14. Построить
линию
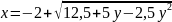 .
.
Задача 15. Составить
уравнение линии, для каждой точки которой
отношение расстояний до точки
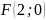 и прямой
и прямой
 равно
равно
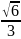 .
Сделать чертеж.
.
Сделать чертеж.
Вариант 4
Задача
1. Написать
разложение вектора
по векторам, если
 ,
,
 ,
,
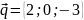 ,
,
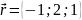 .
.
Задача
2. Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
 ,
,
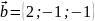 ,
,
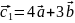 ,
.
,
.
Задача 3. Найти косинус угла между векторами и , если , , .
Задача
4. Компланарны
ли векторы
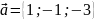 ,
,
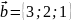 ,
,
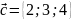 ?
?
Задача
5. Даны
вершины
 ,
,
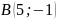 ,
,
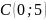 трапеции
трапеции
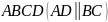 .
Найти координаты вершины
.
Найти координаты вершины
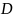 ,
если известно, что диагонали трапеции
взаимно перпендикулярны. Сделать чертеж.
,
если известно, что диагонали трапеции
взаимно перпендикулярны. Сделать чертеж.
Задача
6. Даны
середины сторон треугольника
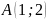 ,
,
,
,
 .
Составить уравнения его сторон.
.
Составить уравнения его сторон.
Задача 14. Составить
уравнение линии, для каждой точки которой
отношение расстояний до точки
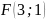 в два раза больше, чем до прямой
в два раза больше, чем до прямой
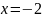 .
Сделать чертеж.
.
Сделать чертеж.
Задача 15. Построить
линию
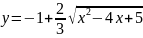 .
.
Вариант 5
Задача
1. Написать
разложение вектора
по векторам, если
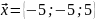 ,
,
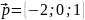 ,
,
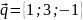 ,
,
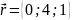 .
.
Задача
2. Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
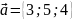 ,
,
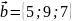 ,
,
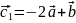 ,
,
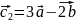 .
.
Задача
3. Найти
косинус угла между векторами
и
,
если
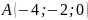 ,
,
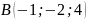 ,
,
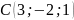 .
.
Задача
4. Компланарны
ли векторы
 ,
,
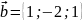 ,
?
,
?
Задача 5. Даны
вершины
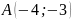 и
и
 и точка
и точка
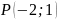 – точка пересечения медиан треугольника.
Составить уравнение высоты, проведенной
через третью вершину
– точка пересечения медиан треугольника.
Составить уравнение высоты, проведенной
через третью вершину
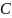 .
Сделать чертеж.
.
Сделать чертеж.
Задача
6. Составить
уравнение прямой, проходящей через
точку пересечения прямых
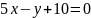 и
и
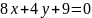 параллельно прямой
параллельно прямой
 .
.
Задача 14. Составить
уравнение линии, каждая точка которой
отстоит от прямой
на
расстоянии, в два раза большем, чем от
точки
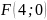 . Сделать чертеж.
. Сделать чертеж.
Задача 15. Построить
линию
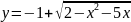 .
.
