7. Матричний простір і метрика

Лінійний простір стає і метричним простором якщо кожній парі елементів: u, v, є, b поставимо у відповідність невід’ємне число ρ(u, v) , що називається метрикою чи відстанню між цими елементами. Метрика визначається як норма різних двох сигналів. Поняття метрики дає можливість судити про те, наскільки добре один з сигналів апроксимує інший.

Задача 7.1

Сигнал u(f) являє собою відрізок синусоїди, що перетворюється в 0 на кінцях інтервалу [0,π]. Висота імпульса U відома. Вибрана амплітуда А прямокутного імпульса v(t) тієї ж тривалості щоб забезпечувати мінімальну відстань між цими сигналами.

Сигнал u(t) можна записати таким чином:

u(t)=U*sin(πt/T), 0<t<T

Квадрат відстані між сигналами буде дорівнювати

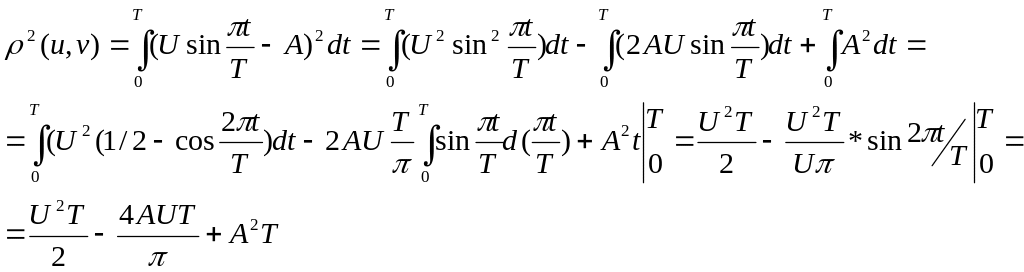
Отже ми одержали

Продиференціювавши одержимо:

Прирівняємо похідну до 0:

=0

A = 2U/π ≈ 0,637U

Необхідно переконатись, що при даному А у нас мінімум. Очевидно, що при похідна від’ємна, а при похідна приймає додатне значення. Отже, можна зробити висновок, що при у нас мінімум. Тоді:

Задача 7.2

Знайти енергію синусоїдального імпульсу та його норму виходячи з умови попередньої задачі

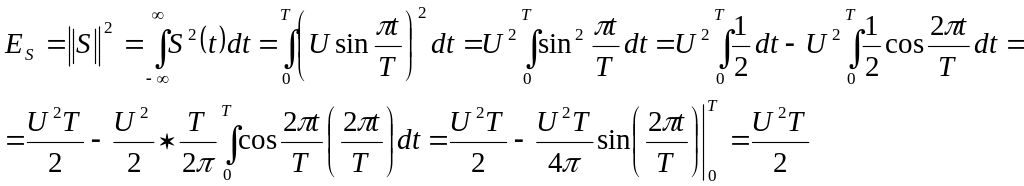
Норма сигнала

Отже в рамках вибраної нами метрики мінімальна відстань між розглянутими сигналами, яку можна досягти, складає від норми синусоїдального імпульса

8. Складання добутків сигналів

Скалярний добуток сигналів U та V

Косинус кута між сигналами

Задача 8.1

Маємо два зсунутих в часі експоненційних імпульси напруги

Знайти скалярний добуток цих сигналів, а також кут між ними.

Енергія цих сигналів, а також норма їх, однакова

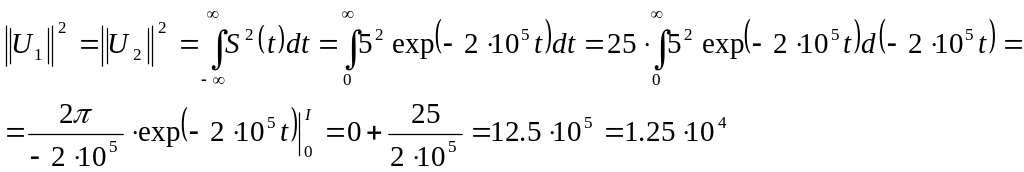
Скалярний добуток сигналів

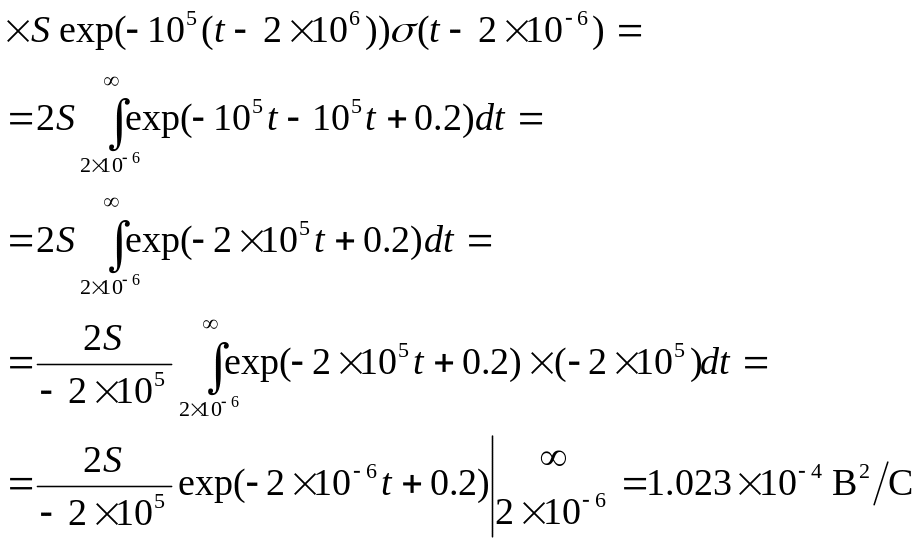
Косинус кута між сигналами:

(В²С)

Скалярний добуток:

(В²С)

Звідси отримаємо:

9. Амплітудна модуляція

У випадку однотонального АМ сигналу обвідна:

де U₀ – амплітуда несучого коливання

М – коефіцієнт модуляції.

Коефіцієнт модуляції виду

ширина спектру АМ сигналу Амплітуда верхньої та нижньої бокової складової однотонального АМ сигналу

Задача 9.1

Амплітуда несучих ВЧ коливань дорівнює 4 В. коефіцієнт модуляції 70%. Знайти максимальне та мінімальне значення АМ сигналу.

Розв’язання

У випадку однотонального АМ сигналу обвідна

S_max = 1 S_min = -1

[ В]

[ В]

Задача 9.2

Амплітуда несучих ВЧ коливань дорівнює 4 В. Максимальне значення АМ сигналу 5 В, а мінімальне 2 В. визначити коефіцієнт модуляції вниз та вгору.

Розв’язання

Коефіцієнт модуляції вгору:

Коефіцієнт модуляції вниз:

Задача 9.3

Низькочастотний модулюючий сигнал має нижню частоту 350 Гц І верхню 4000 Гц. Визначити ширину спектру АМ сигналу якщо частота несучого коливання 1 МГц.

Розв’язання

Гц

Задача 9.4

Амплітуда несучого ВЧ коливання 4 В. Коефіцієнт модуляції 0,65. Розглядається випадок однотональної модуляції. Визначити амплітуду верхньої бокової складової.

Розв'язок

U_ВБ = U₀M/2 = 4*0.65/2 = 1.3 В.