Міністерство освіти і науки України

Черкаський державний технологічний університет

кафедра радіотехніки

Курсова робота

з дисципліни: «Сигнали та процеси»

Перевірив: Виконав:

доц. кафедри р-т. студент 3-го курсу

Даник О. В. ФЕТ РТ – 102

Мякота І. М.

Черкаси 2012 р.

Зміст

Вступ 4

Сигнал — фізичний процес, за допомогою якого відбувається проявлення, тобто генерація, та збереження, перенесення в просторі і часі інформації про предмет, стан, явище, дію тощо. Німецьке слово Signal, латинське signum, тобто знак походить від грецького συμβολον - символ, прикмета, ознака.  Грецьке φυσις означає  - природа, звідси фізика у всій її повноті; -υκα – наука, тобто те, що може бути навчене і повторене в певних умовах. Латинське слово procesus означає проходження, просування вперед; informatio – роз’яснення, від in, тобто роз- і forma – те, що несе вигляд (від грецького φορος, форос– носій) 4

1. Підсилювач малих сигналів з аперіодичним навантаженням. 5

2. Спектральний склад струму у без інерційному елементі, при гармонічному зовнішньому впливові у випадку кусково лінійної апроксимації. 7

3. Амплітудний модулятор 9

4. Функція включення або функція Хевісайда 11

5. Норма та енергія сигналу 14

6. Резонансний підсилювач малих коливань 16

7. Матричний простір і метрика 19

8. Складання добутків сигналів 20

9. Амплітудна модуляція 22

10. Апроксимація характеристик нелінійних елементів 23

Висновок 26

Список використаної літератури: 27

Вступ

Сигнал — фізичний процес, за допомогою якого відбувається проявлення, тобто генерація, та збереження, перенесення в просторі і часі інформації про предмет, стан, явище, дію тощо. Німецьке слово Signal, латинське signum, тобто знак походить від грецького συμβολον - символ, прикмета, ознака.  Грецьке φυσις означає  - природа, звідси фізика у всій її повноті; -υκα – наука, тобто те, що може бути навчене і повторене в певних умовах. Латинське слово procesus означає проходження, просування вперед; informatio – роз’яснення, від in, тобто роз- і forma – те, що несе вигляд (від грецького φορος, форос– носій)

    Властивості усувають невизначеність, проявляють предмети видами сигналів, що в сукупності притаманні  для даної форми матерії і утворюють систему. 

1. Підсилювач малих сигналів з аперіодичним навантаженням.

Рис. 1(а) Рис. 1(б)

1. Спрощена принципова схема.

2. Еквівалентна схема.

R_н – резистор навантаження;

С_п – паразитна ємність.

Метод еквівалентних схем використовується тоді, коли амплітуди змінних напруг у схемі малі наскільки, що можна знехтувати нелінійністю зовнішніх характеристик електронних приладів.

З еквівалентної схеми заміщення випливає, що частотний коефіцієнт передачі схеми дорівнює:

S – крутизна характеристики приладу у робочій точці.

Еквівалентний опір навантаження дорівнює:

R_і – опір приладу.

Модуль коефіцієнту підсилення дорівнює:

Смугу пропуску підсилювача прийнято оцінювати величиною граничної частоти , на якій спостерігається зменшення амплітудно – частотної характеристики (АЧХ) у разів. Гранична частота підсилювача:

Задача 1.1

Підсилювач зібраний за схемою зображеною на рис. 1(б) має такі параметри:

R_н = 1,6 кОм;

S = 20 мА/B;

C_п = 30 пФ;

R_і = 15 кОм;

Обчислити коефіцієнт підсилення на нульовій частоті і смугу пропуску системи.

Розв’язання:

Знаходимо еквівалентний опір навантаження:

Модуль коефіцієнта підсилення на нульовій частоті:

Гранична частота підсилювача:

2. Спектральний склад струму у без інерційному елементі, при гармонічному зовнішньому впливові у випадку кусково лінійної апроксимації.

Характеристики нелінійного елемента:

На нелінійний елемент подана напруга:

Кут відсічки імпульсів струму визначиться з рівності:

Звідки одержуємо

Задача 2.1

Постійна складова та амплітуди гармонік струму обчислюється за формулами у які входять відповідні функції Берга .

Нелінійний елемент має кусково – лінійну вольт – амперну характеристикуз такими параметрами:

U_п = 0.6 В;

S =25мА/B;

До елемента прикладено напругу

U = 0.2 + 0.8 cos ωt (B). Обчислити постійну складову І₀ та першу гармоніку І₁ струму що протікає.

Розв’язання:

Можна знайти:

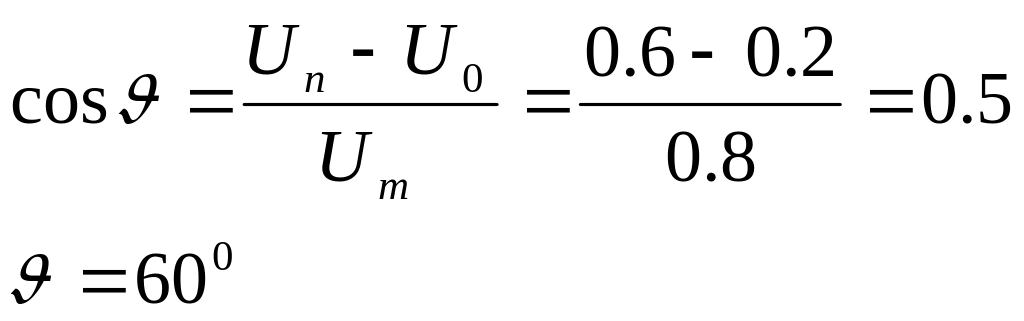
Обчислимо значення функцій Берга:

Тоді можна знайти

3. Амплітудний модулятор

Найпростішим амплітудним модулятором служить однокаскадний підсилювач – пристрій нелінійного типу з резонансним навантаженням.

На вхід подається напруга:

Робоча точка переміщується у такт з низькочастотним модульованим коливанням і відповідно відбувається неперервна зміна кута відсічки несучого сигналу. амплітуда першої гармоніки послідовності імпульсів колекторного струму виявляється непостійною в часі, коливний контур фільтрує колекторний струм виділяючи на виході амплітудно модульований сигнал, тобто коливання з амплітудою, що змінюється пропорційно корисному моделюючому сигналу.

Задача 3.1

Транзистор що використовується в схемі модулятора, має злам характеристики в точці U_п=0.6 В, амплітуда коливань несучої частоти на вході U_{m нес}=0.4 В, амплітуда моделюючого сигналу U_{m мод}=0.1 В, початковий зсув U₀=0.6 В. визначити коефіцієнт амплітудної модуляції М у даній схемі.

Розв’язання:

Коли косинусоїдальні імпульси не модульовані , тобто U_{m мод}=0 , то кут відсічки буде рівним:

У випадку коли U_{m мод} ≠ 0, положення робочої точки змінюється у межах від:

U₀ + U_{m мод}=0.7 В;

до

U₀ - U_{m мод}=0.5 В;

тоді кут відсічки буде змінюватись так:

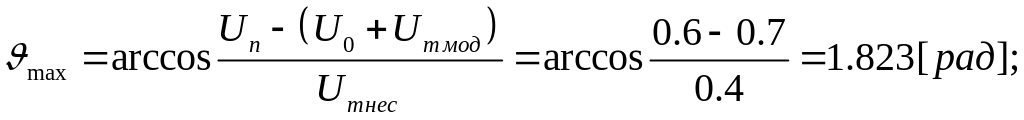
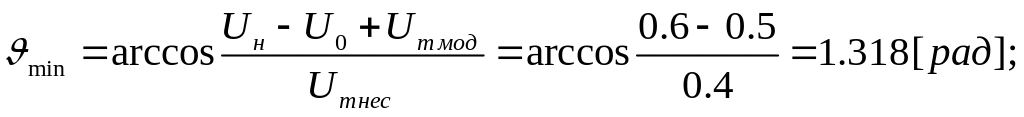
амплітуда першої гармоніки колекторного струму дорівнює

тобто амплітуда першої гармоніки колекторного струму пропорційна функції яка залежить від кута відсічки, а отже змінюється у межах від:

;

до

;

Виходячи з цього, знаходимо коефіцієнт модуляції вихідного сигналу

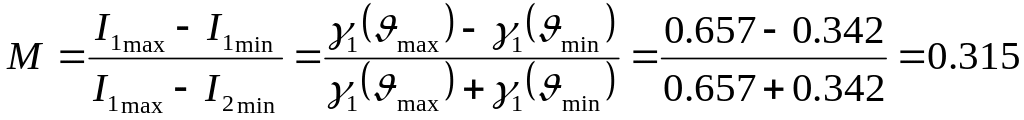
4. Функція включення або функція Хевісайда

Розглянемо сигнал заданий системою рівностей:

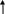
така функція процес переходу деякого фізичного об’єкта з «нульового» в «одиничний» стан, причому цей перехід здійснюється за лінійним законом, за час , якщо параметр спрямувати до нуля, то при переході до границі, зміна одного стану на інший буде здійснюватись миттєво математична модель цього граничного сигналу одержала назву функції включення або функції Хевісайда.

за допомогою функції зручно описувати процеси комутації у електричних колах, в теоретичній радіотехніці функцію включення дуже широко використовують для опису розривних, зокрема імпульсних сигналів.

Якщо зсунута відносно початку відліку часу на величину t₀ то