Варіант 1

1. На складі взяли 5 мішків борошна І ґатунку і 7 мішків борошна ІІ ґатунку. Довільні 6 мішків з 12 витратили на приготування одного з видів поляниці. Знайти ймовірність того, що половина з цих 6 мішків борошна виявилась борошном І ґатунку.

2. Відбувається два постріли по мішені. Чи будуть несумісними дві події: відбулося хоча б одне влучення або був хоча б один промах?

3. Імовірність того, що один з трьох ліфтів виявиться в даний момент на першому поверсі, дорівнює 0,1. Яка ймовірність того, що хоча б один ліфт виявиться на першому поверсі?

4. 30 % приладів складає спеціаліст високої кваліфікації і 70 % - середньої. Надійність приладу, складеного спеціалістом високої кваліфікації, дорівнює 0,9, приладу, складеного спеціалістом середньої кваліфікації, - 0,8. Взятий прилад працює безвідмовно. Визначити ймовірність того, що його складав спеціаліст високої кваліфікації.

5. Імовірність того, що витрата води на деякому підприємстві виявиться нормальною, дорівнює 0,75. Знайти ймовірність того, що в найближчі 6 днів витрата води буде нормальною протягом 3 днів.

6. При деякому випробуванні ймовірність позитивного наслідку дорівнює 0,8. Знайти ймовірність того, що число позитивних наслідків при 200 випробуваннях буде не меншим за 170.

7. Закон розподілу дискретної випадкової величини Х задано таблицею:

Х	-7	-6	-5	-4	-3
р	0,2	0,25	0,1	0,15	0,3

Знайти функцію розподілу випадкової величини Х і побудувати її графік. Знайти середнє квадратичне відхилення випадкової величини Х.

8. Інтегральна функція розподілу випадкової величини Х має вигляд:

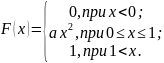
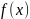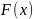Потрібно: а) знайти коефіцієнт а; б) знайти функцію щільності розподілу ; в) побудувати графіки функцій і ; г) знайти ймовірність того, що випадкова величина набуде значення з інтервалу (0,25; 0,5).

9. Відомо, що випадкова величина може набувати значення 1, 2 і 3. Знайти імовірність цих значень, якщо математичне сподівання цієї випадкової величини дорівнює 1,8, а дисперсія 0,56.

10. 50 % помилок приладу не виходить за межі . Знайти процент помилок приладу, що не виходить за межі , коли відомо, що прилад не має систематичних помилок. Випадкові помилки підпорядковуються нормальному розподілу.

11. Дисперсія кожної з 2500 незалежних випадкових величин не перевищує 5. Оцінити ймовірність того, що відхилення середнього арифметичного цих випадкових величин від середнього арифметичного їх математичного сподівання не перевищить 0,4.

12. Знайти коефіцієнт кореляції випадкових величин Х і У, якщо відомий двовимірний розподіл цих величин:

У Х	1	2	3	4
-2	0,1	0,1	0,05	-
-1	0,05	0,2	0,2	0,05
0	-	-	0,05	0,2

Варіант 2

1. Виготовлено 6 замків, ключі до яких змішані. Випадково беруть два ключі і два замки. Яка імовірність того, що навмання взяті ключі підійдуть до взятих замків?

2. Здійснюється три постріли по мішені. Перелічити елементарні події, з яких складаються події, що їх дістаємо як суму і як добуток таких подій: відбулося рівно одне попадання; при повторному пострілі не було попадання.

3. Яка ймовірність того, що довільно взяті 3 людини народилися в один і той самий день тижня?

4. У ящику 12 сталевих і 8 мідних деталей. Імовірність того, що сталева деталь буде придатною при складанні, дорівнює 0,95, мідна – 0,97. Знайти імовірність того, що випадково взята з ящика деталь буде придатною.

5. Студенту задають 6 питань. На кожне питання дано 4 можливих відповіді, з-поміж яких необхідно вибрати одну правильну. Яка ймовірність того, що при простому вгадуванні студент відповість вірно не менш ніж 5 питань?

6. Яка ймовірність того, що серед 200 осіб виявиться щонайменше 4 лівші, якщо в середньому лівші становлять 1 %?

7. Закон розподілу дискретної випадкової величини Х задано таблицею:

Х	1	3	5	7	9	11
р	0,1	0,15	0,1	0,15	0,1	0,4

Знайти функцію розподілу випадкової величини Х і побудувати її графік. Знайти середнє квадратичне відхилення випадкової величини Х.

8. Випадкову величину Х задано функцією щільності розподілу:

Потрібно: а) знайти коефіцієнт а; б) знайти функцію розподілу ; в) побудувати графіки функцій і ; г) знайти математичне сподівання і дисперсію випадкової величини Х.

9. Екзаменатор пропонує студентові додаткові питання. Імовірність того, що студент відповість на задане питання – 0,9. Викладач перериває іспит, тільки-но студент невірно відповідає на питання або коли кількість питань досягає 5. Знайти закон розподілу кількості додаткових питань. Визначити математичне сподівання випадкової величини.

10. Імовірність набуття випадковою величиною, що розподілена нормально, значення з інтервалу (-5;5), дорівнює 0,0455. Знайти дисперсію розподілу, коли відомо, що математичне сподівання дорівнює 0.

11. Вивчено 100 путівок різних автомобілів певної автобази. Встановлено, що середня довжина маршруту дорівнює 43,7 км при середньому квадратичному відхиленні 15,4 км. Визначити з імовірністю 0,8859, в яких межах виявиться середня довжина всіх маршрутів, пройдених автомобілями бази.

12. Знайти коефіцієнт кореляції випадкових величин Х і У, якщо відомий двовимірний розподіл цих величин:

У Х	-2	-1	0
2	0,3	-	-
3	-	0,1	0,2
4	-	0,1	0,3

Варіант 3

1. Четверо робітників прийшли на роботу до цеху, в якому працюють 12 робітників. З усіх робітників сформували випадковим чином 2 групи по 8 осіб у кожній. Знайти ймовірність того, що робітники, які щойно прийшли, будуть в одній групі.

2. Монета підкидається 3 рази. Чи є незалежними події: поява герба при перших двох підкиданнях; поява цифри в результаті хоча б одного з останніх підкидань?

3. Знайти ймовірність того, що виріб який складається з трьох деталей, вийшов із ладу через несправність не менш ніж двох деталей, якщо ймовірність виходу з ладу деталей дорівнює 0,2; 0,3; 0,1.

4. З першого автомата на склад надходить 40 % , з другого – 30 %, з третього – 20 %, з четвертого – 10% деталей. Серед деталей першого автомата 0,1 % бракованих, другого – 0,2 %, третього – 0,5 %, четвертого – 0,5 %. Знайти ймовірність того, що на склад надійшла бракована деталь.

5. Завод, що виготовляє радіолампи, дає 5 % браку. На випробування взято 3 радіолампи. Знайти ймовірність того, що серед них буде не більш як дві зіпсовані.

6. Імовірність неточного складання приладу 0,2. Знайти імовірність того, що серед 500 приладів виявиться від 410 до 430 точних.

7. Закон розподілу дискретної випадкової величини х задано таблицею:

Х	-2	0	2	4	6	8
р	0,05	0,2	0,15	0,1	0,25	0,25

Знайти функцію розподілу випадкової величини Х і побудувати її графік. Знайти середнє квадратичне відхилення випадкової величини Х.

8. Випадкову величину х задано функцією щільності розподілу:

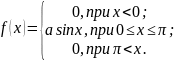
Потрібно: а) знайти коефіцієнт а; б) знайти функцію розподілу ; в) побудувати графіки функцій і ; г) знайти ймовірність того, що випадкова величина Х набуде значення з інтервалу .

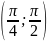9. У двох ящиках лежать по десять куль із цифрами. У першому лежить одна куля з цифрою 1, 5 куль із цифрою 2 і 4 кулі із цифрою 3. У другому ящику лежать дві кулі з цифрою 1, 7 куль з цифрою 2 і 1 куля з цифрою 3. Одночасно виймають по одній кулі з обох ящиків. Добуток цифр на цих кулях є випадковою величиною. Знайти закон розподілу і математичне сподівання цієї випадкової величини.

10. Розподіл заводів за процентом виконання плану підпорядковується закону нормального розподілу із середнім арифметичним 103,3 % і середнім квадратичним відхиленням 1,5 %. Визначити, яка частина заводів не виконує план.

11. Середнє значення швидкості вітру біля землі в даному пункті дорівнює 16 км/год. Закон розподілу швидкостей вітру невідомий. Оцінити ймовірність того, що швидкість вітру в цьому пункті в даний момент часу не перевищує 80 км/год.

12. Знайти коефіцієнт кореляції випадкових величин х і у, якщо відомий двовимірний розподіл цих величин:

У Х	-2	-1	0
0	0,3	0,05	-
1	0,05	0,2	0,05
2	-	0,05	0,2
3	-	-	0,1

Варіант 4