7. Второе начало термодинамики

Как отмечалось выше, первое начало термодинамики представляет собой количественное выражение закона сохранения и превращения энергии, оно позволяет составить энергетический баланс исследуемых процессов, но не определяет направление их протекания. Условия осуществления и направленности протекания процессов определяются на основании второго начала термодинамики.

В совокупности первое и второе начало термодинамики являются фундаментом в построении теории тепловых машин и технической термодинамики в целом.

Второе начало классической термодинамики обычно формулируется как объединенный принцип существования и возрастания некоторой функции состояния тел и сложных систем, названной энтропией (термин энтропия предложен Р. Клаузиусом: еn – в, внутрь и trope или tropos – обращение, путь; в целом – обращение внутрь, мера обесценения энергии).

Математическое выражение второго начала классической термодинамики может быть представлено в виде следующего выражения:

. (155)

Н.И. Белоконь справедливо заметил, что принципы существования и возрастании энтропии различны по содержанию и значимости и предложил рассматривать эти принципы раздельно.

Принцип существования энтропии справедлив для равновесных термодинамических систем и распространяется на любые процессы – обратимые и необратимые. Принцип существования энтропии и абсолютной температуры как термодинамических функций состояния равновесных систем, по терминологии проф. Н.И. Белоконь, был назван вторым началом термостатики.

Принцип возрастания энтропии характеризует только наиболее вероятное направление течения реальных процессов и, следовательно, имеет несомненно меньшую область применения, чем принцип существования энтропии. Принцип возрастания энтропии изолированных систем при протекании в них реальных процессов Н.И. Белоконь назвал вторым началом термодинамики.

Второе начало термостатики

В качестве постулата второго начала термостатики используется утверждение, что «температура есть единственная функция состояния, определяющая направление самопроизвольного теплообмена».

Для вывода математического выражения второго начала термостатики рассмотрим адиабатно изолированную систему, состоящую из термически сопряженных тел (рис. 13). Первое тело (I) - любое тело (например, реальный газ), совершает произвольные процессы - обратимые и необратимые, второе тело (II) - контрольное тело - идеальный газ, совершает обратимый круговой процесс. Оба тела в каждый момент имеют одинаковую температуру (t_I = t_II = t).

Рис. 13. Адиабатно изолированная система двух термически сопряженных тел

Первое и второе тело осуществляют разнообразные процессы изменения состояния, к ним извне подводится (или отводится) работа, между телами происходит теплообмен, но для адиабатно изолированной системы выполняется обязательное условие

. (156)

Разделим уравнение (156) на некоторую функцию, зависящую только от температуры (t). Для идеального газа эта функция равна абсолютной температуре (t_II) = T_II . С учетом равенства температур двух тел получаем

. (157)

Так как тела I и II возвращаются в исходное состояние одновременно (согласно теореме теплового равновесия тел в равновесных круговых процессах) последнее уравнение можно интегрировать по замкнутому контуру

. (158)

Второй интеграл по замкнутому контуру для идеального газа, как интеграл функции состояния, равен нулю

. (159)

Поэтому и первый круговой интеграл в уравнении (158) также равен нулю

. (160)

Если круговой интеграл равен нулю, то это значит, что подынтегральное выражение представляет из себя полный дифференциал некоторой функции состояния, названной энтропией ( ), а функция (t_I) является интегрирующим делителем

. (161)

Так как тело I - любое тело и свойства тел I и II независимы, полученное выражение (161) распространяется на все равновесные процессы изменения состояния любых систем. Выбранная функция (t), которая не зависит от вида тел, называется абсолютной температурой (t)= Т, а температурная шкала называется абсолютной термодинамической.

Таким образом, получаем математическое выражение второго начала термостатики - принципа существования энтропии и абсолютной температуры для любых равновесных систем

(162)

и для 1 кг системы

. (163)

Второе начало термостатики утверждает принцип существования энтропии и абсолютной температуры как функции состояния любой равновесной термодинамической системы, совершающей обратимые или необратимые процессы.

Следствия второго начала термостатики

Следствия второго начала термостатики широко применяются в термодинамических расчетах и формулируются на основе анализа его математического выражения (162), (163).

Следствие I. Совместное выражение первого начала термодинамики и второго начала термостатики позволяет получить дифференциальное уравнение термодинамики, которое связывает между собой все термодинамические свойства веществ

T ds= c_v dT + = c_p dT + . (164)

Следствие II. Координаты Т - S являются универсальными координатами термодинамического теплообмена.

Рассмотрим процесс 1-2 в координатах Т-S и выделим на нем элементарный участок с температурой Т и изменением энтропии dS (рис. 14).

Рис. 14. Термодинамический процесс в координатах T-S

Исходя из математического выражения второго начала термостатики площадь под кривой элементарного участка процесса равна подводимому (отводимому) количеству теплоты

Q = TdS. (165)

При этом полное количество теплоты, подведенной или отведенной от системы в процессе 1-2, определяется следующим образом:

Q_1,2 = . (166)

Если из-под знака интеграла в соотношении (166) вынести среднюю температуру конечного процесса T_m , то количество теплоты в процессе может быть определено по соотношению

Q_1,2 = T_m(S₂ - S₁). (167)

Как видно из выражения (166) и рис. 15, знак теплообмена определяется знаком изменения энтропии. Процессы, протекающие с увеличением энтропии, сопровождаются подводом теплоты. Процессы, протекающие с уменьшением энтропии - отводом теплоты. Независимо от природы рабочего тела площадь под кривой процесса в координатах Т-S равна количеству подведенной или отведенной теплоты.

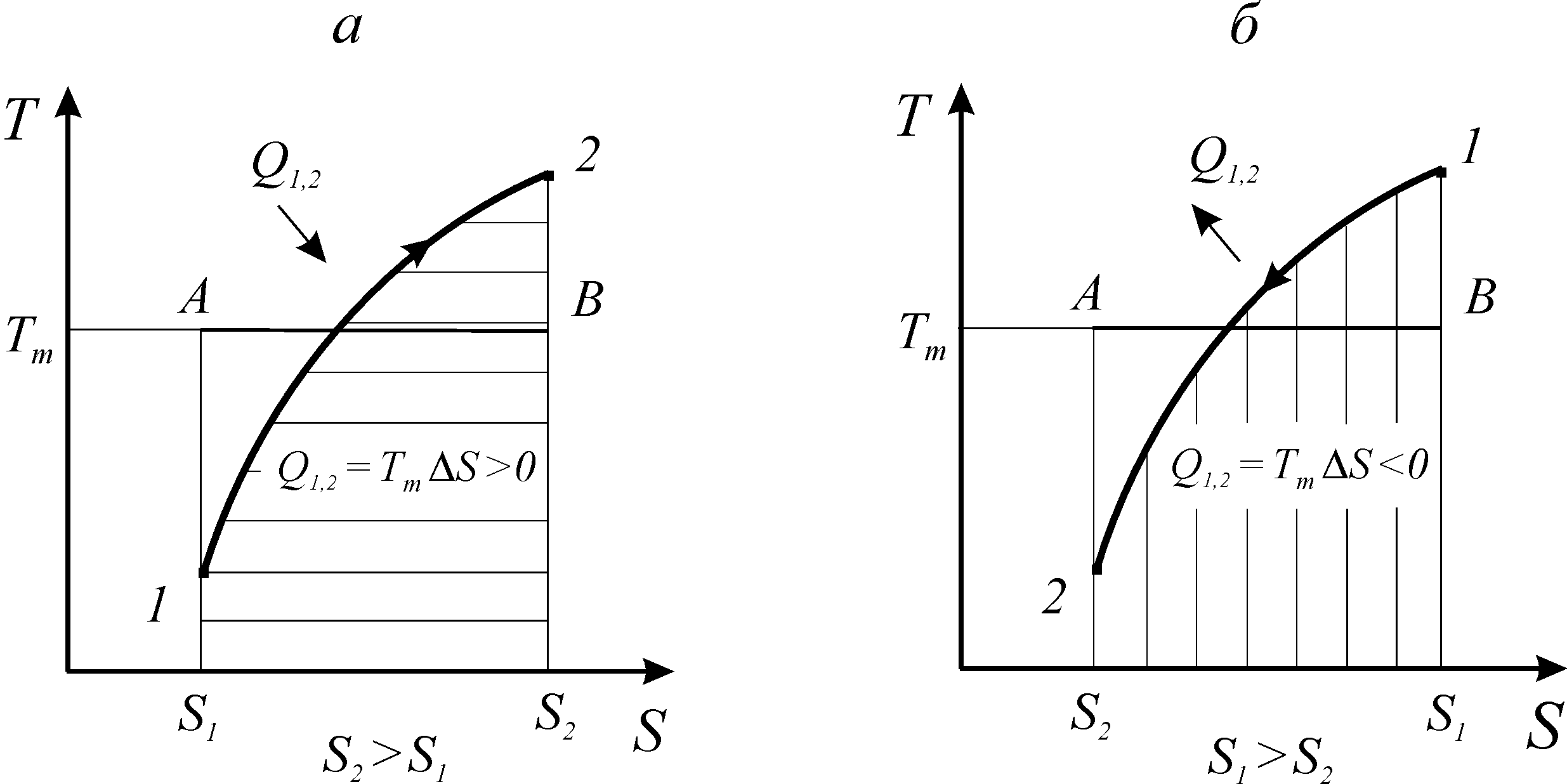
Рис. 15. Теплообмен в термодинамических процессах

Следствие III. Адиабатный процесс является процессом изоэнтропийным.

Так как в адиабатном процессе теплообмен отсутствует (Q = 0), то, согласно второму началу термостатики (162), в таком процессе изменение энтропии dS = 0 (S = idem). Согласно этому следствию, показатель адиабатного процесса ( ) равен показателю изоэнтропийного процесса ( )

. (168)

Следствие IV. Коэффициент полезного действия и холодильный коэффициент термодинамических циклов тепловых машин не зависят от вида цикла и природы рабочего тела, а определяются лишь средними абсолютными температурами рабочего тела в процессах подвода и отвода теплоты.

Рассмотрим термодинамические циклы в координатах Т-S: прямой цикл (цикл теплового двигателя) 1-А-2-В-1 (а) и обратный цикл (цикл холодильной машины) 1-А-2-B-1 (б) (рис. 16).

В процессе 1-А-2 теплота подводится к рабочему телу. Количество подводимой теплоты соответствует на диаграмме горизонтально заштрихованной площади. Вертикально заштрихованная площадь соответствует количеству отведенной теплоты от рабочего тела в процессе 2-В-1.

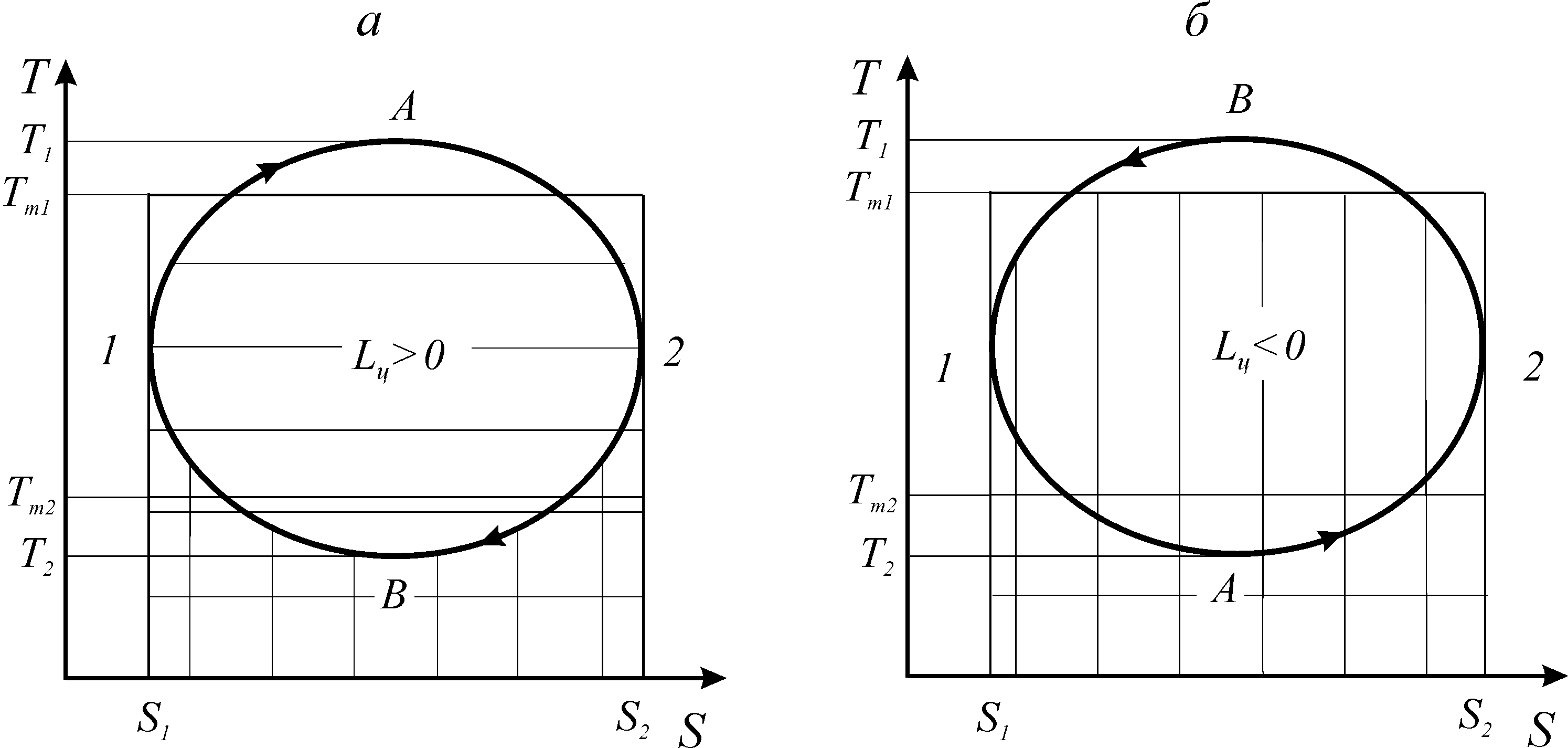
Рис. 16. Прямой и обратный циклы в координатах Т-S

Средние температуры рабочего тела в процессах подвода и отвода теплоты в цикле теплового двигателя обозначим Т_m1 и Т_m2 соответственно (рис. 16а). Согласно выражения (167), количества подведенной и отведенной теплоты определяется по следующим соотношениям:

Q₁= = T_m1 ( S₂ - S₁ ) = T_m1 S_1,2; (169)

Q₂= = T_m2( S₂ - S₁ ) = T_m2 S_1,2, (170)

а коэффициент полезного действия любого термодинамического цикла теплового двигателя может быть найден из выражения

= =1 - . (171)

В результате аналогичных рассуждений получаем выражение для определения холодильного коэффициента термодинамического цикла холодильной машины (рис. 16б)

= = . (172)

Полученные выражения (171), (172) свидетельствуют о том, что КПД и холодильный коэффициент термодинамических циклов тепловых машин определяются только средними абсолютными температурами рабочего тела в процессах подвода и отвода теплоты.

Из уравнений (171), (172) следует также, что для любого термо-динамического цикла тепловых машин выполняется следующее соотношение:

. (173)

Следствие V. Коэффициент полезного действия и холодильный коэффициент цикла Карно всегда выше этих коэффициентов эффективности для любых других термодинамических циклов тепловых машин, осуществляемых в одинаковом диапазоне предельных температур рабочего тела ( ).

Это следствие вытекает из анализа соотношений по определению КПД цикла Карно (153) и любого термодинамического цикла (171) теплового двигателя. Вследствие того, что Т₁ >Т_m1 и Т₂ < Т_m2 (рис. 16а),

. (174)

Аналогичный вывод можно сделать и при сравнении холодильных коэффициентов обратных циклов

. (175)

Рассматриваемое следствие утверждает, что цикл Карно является эталонным циклом, по сравнению с которым можно определить термодинамическое совершенство любого цикла, осуществляемого в заданном интервале предельных значений температур рабочего тела.

Следствие VI. Изменение энтропии системы равно сумме изменений энтропии всех тел, входящих в систему (теорема аддитивности энтропии).

Количество теплоты, полученное в элементарном процессе системой, состоящей из тел, можно определить из соотношения

, (176)

что и подтверждает справедливость сформулированного следствия

. (177)

Второе начало термодинамики и его следствия

Все явления природы, связанные с превращением энергии имеют необратимый характер. Обобщающим законом необратимости процессов в природе является принцип возрастания энтропии изолированных систем. В основу второго начала термодинамики положен постулат, утверждающих необратимость реальных процессов и имеющий ряд равнозначных формулировок:

• теплота не может самопроизвольно передаваться от холодного тела к более нагретому (Р. Клаузиус, 1850 г.);

• невозможно построить периодически действующую машину, вся деятельность которой сводилась бы к выполнению механической работы и охлаждению теплового источника (В. Томсон – Кельвин, 1852 г.);

• любой реальный самопроизвольный процесс является необратимым (М. Планк, 1926 г.);

• работа может быть непосредственно и полностью превращена в теплоту путем трения или электронагрева.

Эти формулировки подчеркивают специфичность теплоты при ее превращениях. В теплоту полностью превращаются все виды энергии. Превращения же теплоты всегда сопровождаются процессами, компенсирующими эти превращения. В тепловом двигателе такой компенсацией является передача некоторой части теплоты источнику низшей температуры (холодному источнику); в холодильных машинах такой компенсацией являются затраты работы.

Анализ различных формулировок постулата второго начала термодинамики приводит к некоторым весьма важным следствиям.

Следствие I. Невозможно осуществление полного превращения теплоты работу, т.е. нельзя создать вечный двигатель второго рода (Perpetuum mobile II рода) с коэффициентом полезного действия равным единице.

Это следствие вытекает из постулата в формулировке Томсона-Кельвина, согласно которой всякий тепловой двигатель должен иметь как минимум два источника теплоты с различной температурой Т₁ и Т₂. Следовательно, всегда  _> 0 и поэтому

. (178)

Следствие II. КПД реального теплового двигателя и холодильный коэффициент реальной холодильной машины, в которых осуществляются циклы при температурах внешних источников Т₁ и Т₂ , всегда меньше КПД и холодильного коэффициента обратимых тепловых машин, циклы в которых осуществляются между теми же внешними источниками:

 < _обр ;  < _обр . (179)

Снижение КПД и холодильного коэффициента реальных тепловых машин по сравнению с _обр и _обр обратимой тепловой машины обусловлено прямым превращением части работы в теплоту (необратимые потери работы) и наличием конечной разности температур между внешними источниками теплоты и рабочим телом.

Следствие III. Абсолютный нуль по термодинамической абсолютной шкале температур (шкала Кельвина) недостижим ( ).

Это следствие вытекает из анализа соотношения по определению КПД цикла Карно (153) и постулата второго начала термодинамики в формулировке Томсона-Кельвина. Поскольку КПД любого теплового двигателя и даже работающего по эталонному циклу Карно всегда меньше 1

, (180)

и в случае, если горячий источник теплоты имеет положительную температуру по термодинамической абсолютной шкале температур ( ), справедливо утверждение

. (181)

Математическое выражение второго начала термодинамики

Наиболее наглядно принцип возрастания энтропии доказывается на основе изучения круговых процессов тепловых машин.

Рассмотрим реальный процесс 1-2 на диаграмме Т-S (рис. 17).

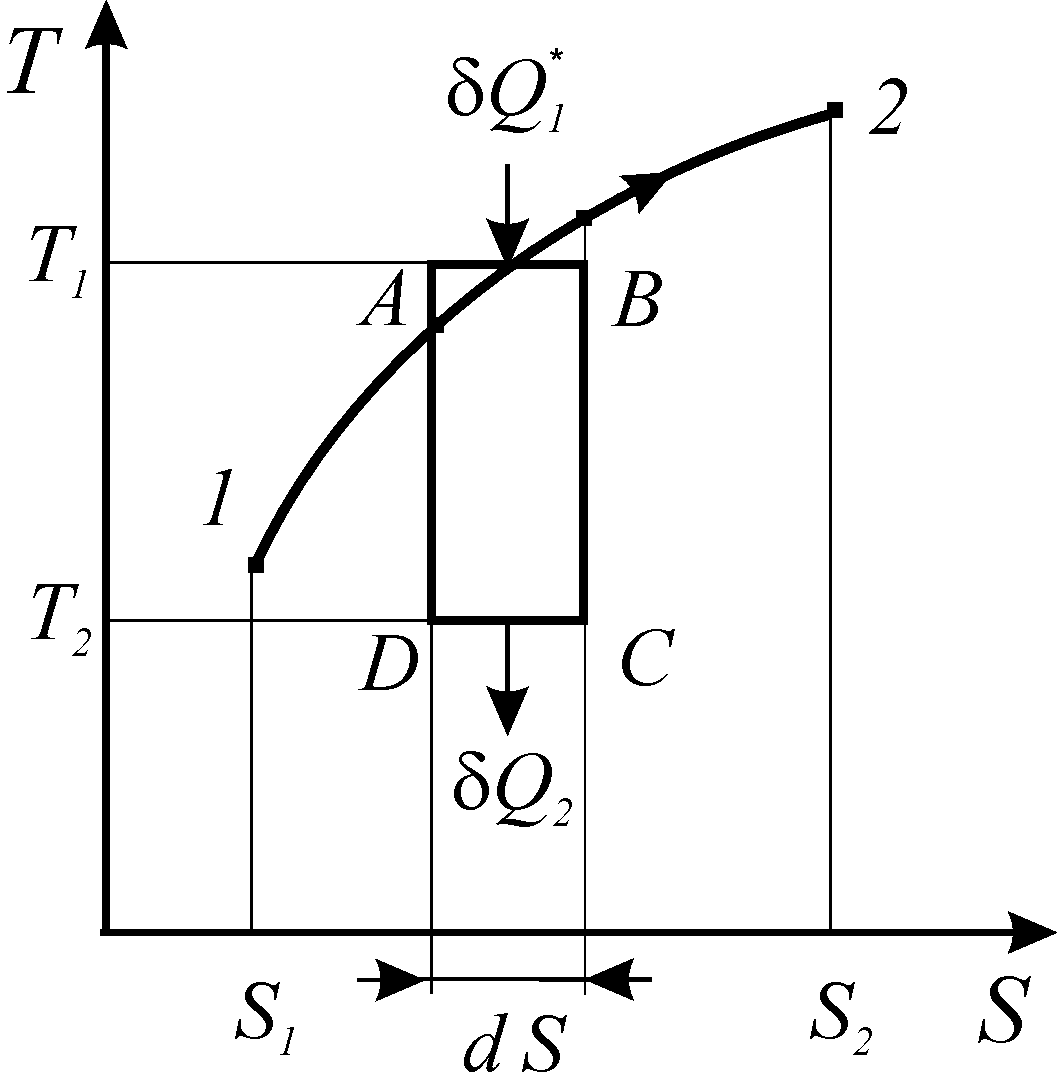
Рис. 17. К доказательству второго начала термодинамики

Выделим на кривой процесса элементарный участок А-В и к нему добавим три обратимых процесса: адиабату расширения В-С, изотерму отвода теплоты С-D и адиабату сжатия D-А. Полученный цикл А-В-С-D, в целом, необратим из-за реального процесса 1-2, а следовательно его КПД меньше, чем у цикла Карно

. (182)

В выражении (182) справедлив знак неравенства, если рассматриваемый цикл (А-В-С-D) необратим, и знак равенства, если рассматривается обратимый цикл.

После преобразования выражения (182), для любых циклов получаем:

; (183)

; (184)

. (185)

Учитывая то, что количество теплоты, подведенной к рабочему телу извне, имеет положительный знак ( ), а количество теплоты, отведенной от рабочего тела – отрицательно ( ), из выражения (185) получаем следующее неравенство

. (186)

Для рабочего тела в обратимом процессе CD согласно II началу термостатики

. (187)

Согласно условию замыкания кругового процесса (A-B-C-D-A), интегральное изменение любой функции состояния рабочего тела равно нулю, а, так как энтропия изменяется только в процессах A-B и C-D, это условие можно представить следующим образом:

. (188)

Выражение (186) с учетом соотношений (187), (188) приобретает следующий вид:

(189)

или

. (189а)

Вследствие того, что при выводе рассматривался произвольный процесс и не было ограничений на свойства рабочего тела, результаты вывода (выражение 189а) имеют самый общий характер.

Итоговое математическое выражение второго начала термодинамики в дифференциальной и интегральной формах, как принципа возрастания энтропии изолированных систем имеет следующий вид:

; (190)

. (191)

Знак неравенства в выражениях (190), (191) справедлив в случае, когда в системе происходят реальные необратимые процессы, а равенства – при протекании обратимых процессов.

Если совместить математические выражения второго начала термостатики (162) и второго начала термодинамики (190) то получается следующее соотношение:

, (192)

из которого вытекает следующее утверждение:

dS^** = > 0, (193)

а при условии, что абсолютная температура всегда положительна (T > 0), непосредственно следует принцип необратимости внутреннего теплообмена

. (194)

Данное неравенство (194) свидетельствует о том, что внутренний теплообмен Q^** в реальных процессах имеет только положительный знак, т.е. работа и количество теплоты в действительных процессах всегда меньше работы и теплоты в обратимом процессе. Затраты работы на необратимые потери в реальных процессах, равные количеству теплоты внутреннего теплообмена , однозначно способствуют росту энтропии.

Для изолированной системы, у которой отсутствует теплообмен с окружающей средой ( ), неравенства (190), (191) принимают вид

dS_изол  0, S₂  S₂ . (195)

Анализ выражения (195) наглядно показывает, что какие бы процессы не протекали в изолированной системе, ее энтропия не может уменьшаться. При протекании в изолированной системе необратимых процессов энтропия системы возрастает; если же в ней протекают обратимые процессы, то энтропия системы остается неизменной.

Из анализа математического выражения второго начала термодинамики (191) следует, что в том случае, когда в изолированной системе протекают самопроизвольные процессы, сопровождающиеся выравниванием температуры различных ее частей, энтропия системы увеличивается. Отсюда следует, что энтропия является величиной, определяющей близость изолированной системы к состоянию равновесия.

Все реальные процессы, происходящие в природе, необратимы и сопровождаются частичным переходом различных видов энергии в теплоту, которая рассеивается в пространстве. Обратный же переход теплоты в другие виды энергии возможен только при наличии разности температур. Р. Клаузиус ввел энтропию как меру «деградации» энергии. Направленность протекания процессов во Вселенной, по версии Клаузиуса, должна привести к тепловому равновесию, из которого Вселенная выйти самостоятельно не может. Состояние Вселенной, при котором в ней устанавливается тепловое равновесие, было названо состоянием «тепловой смерти Вселенной».

Следует отметить, что свои выводы Р. Клаузиус сделал, рассматривая Вселенную как изолированную систему. Современная наука опровергает это предположение. Кроме того, математическое выражение второго начала термодинамики и разнообразие процессов, протекающих во Вселенной, не исключают возможности существования процессов, имеющих отрицательный знак внутреннего теплообмена ( ). Эти обстоятельства подвергают сомнению правомерность теории Р. Клаузиуса о «тепловой смерти Вселенной».