2. Физическое состояние вещества, фазовая диаграмма чистого вещества

Различают три агрегатных состояния простых систем: твердое, жидкое и газовое.

С помощью фазовой диаграммы можно проследить переход тела из одного агрегатного состояния в другое. Рассмотрим диаграмму фазовых состояний чистого вещества (рис.3).

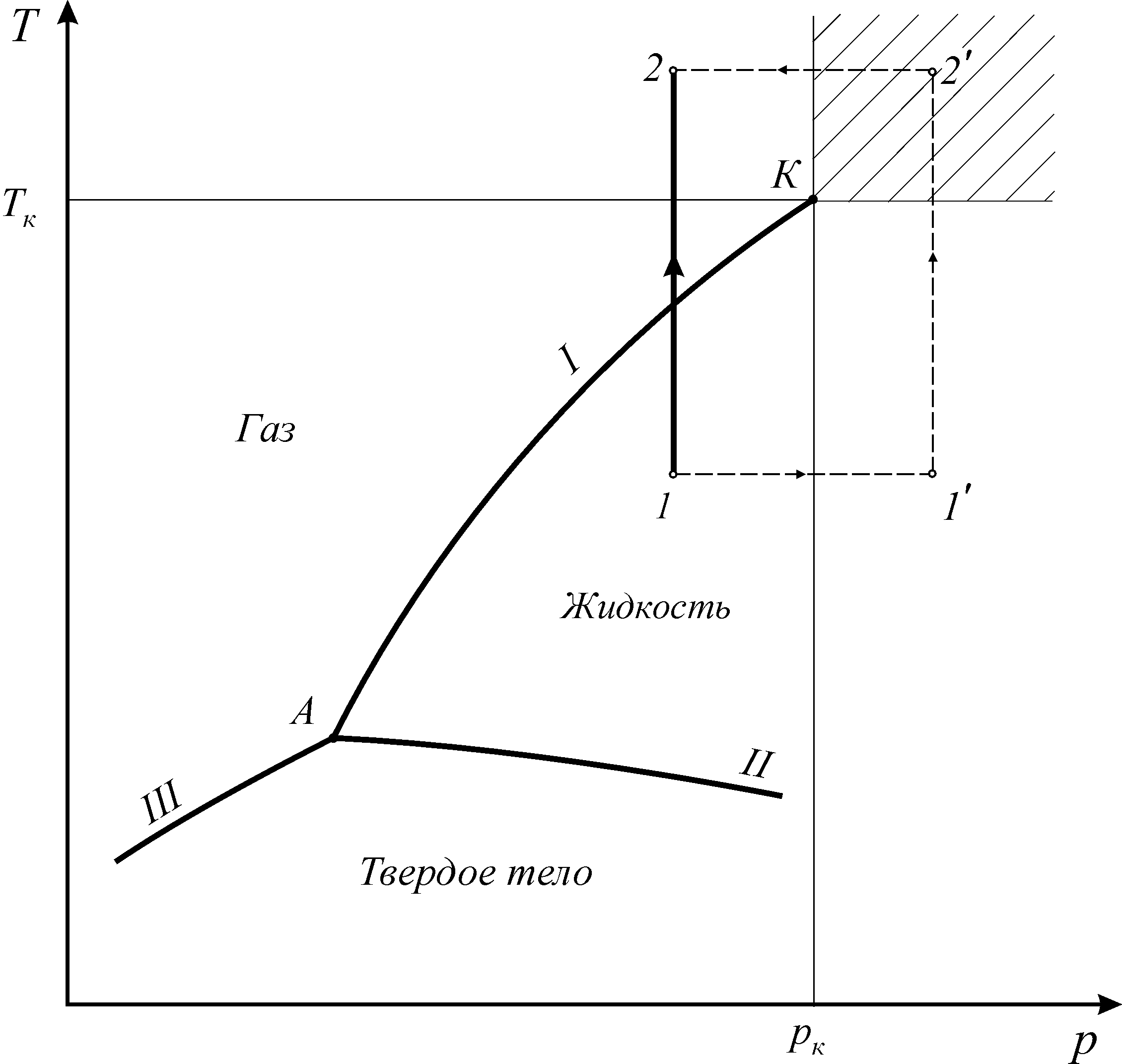
Рис. 3. Диаграмма фазовых состояний чистого вещества

Линии фазовых превращений (испарение - I, плавление - II, сублимации - III) отображают термодинамическое равновесие двухфазных систем и делят диаграмму на области различных агрегатных состояний.

Фазами системы называются области, ограниченные поверхностями раздела. На линиях фазовых превращений существует однозначная зависимость между давлением и температурой. Эти линии пересекаются в тройной точке, где вещество одновременно находится в трех агрегатных состояниях. Параметры тройной точки принадлежат к термодинамическим константам вещества.

Энергетической границей между жидкостью и паром является теплота испарения, а между твердым телом и жидкостью – теплота плавления. Так как процессы испарения и плавления протекают при постоянной температуре, то теплоты испарения, плавления и сублимации есть теплоты изотермических превращений. Теплота фазового перехода обозначается символом .

Наибольший интерес для проведения технических расчетов в термодинамике представляют газ и жидкость. При увеличении давления термодинамическое различие в их свойствах заметно уменьшается и в критической точке исчезает полностью.

Критические параметры являются важнейшими термодинамическими постоянными вещества. Понятие критической температуры введено Д. И. Менделеевым. Критическая температура – это температура, при которой и выше которой газ никаким сжатием не может быть переведен в жидкое состояние. Критическое давление – это такое давление, при котором и выше которого жидкость невозможно перевести в газообразное состояние, а критический объем представляет собой максимальный объем данного количества вещества в жидком состоянии.

В закритической области ( ) вещество может находиться только в однофазном состоянии. Переход из состояния 1 в состояние 2 возможен кратчайшим путем по линии 1-2. Можно этот переход осуществить через закритическую область, то есть без изменения агрегатного состояния, например по линии (рис. 3).

Условным признаком непрерывности однофазного состояния вещества является возможность перехода его из любого однофазного исходного состояния в другое однофазное состояние путем непрерывных изменений параметров состояния, минуя фазовые энергетические барьеры.

Поэтому в принципе, для простых тел (однородных систем) должно существовать единое уравнение состояния , описывающее любое однофазное состояние вещества. Такого уравнения пока еще не получено. Ниже рассмотрим уравнения состояния идеальных и реальных газов.

3. Законы и уравнение состояния идеальных газов. Уравнения состояния реального газа

Идеальные газы

Идеальными называются газы, у которых молекулы представляют собой материальные точки и между молекулами отсутствуют силы взаимодействия.

При относительно низком давлении и высоких температурах реальные газы имеют малую плотность и, с известным допущением, могут рассматриваться как газы идеальные.

Законы идеальных газов были установлены в XVII - XIX столетиях исследователями, изучавшими экспериментальным путем поведение газов при давлениях, близких к атмосферному.

Закон Бойля (1662 г.) – Мариотта (1676 г.): произведение абсолютного давления на удельный объем идеального газа при неизменной температуре есть величина постоянная, т.е. произведение абсолютного давления на удельный объем идеального газа зависит только от температуры газа:

при t = idem рv= idem. (24)

Закон Гей Люссака (1802 г.) – относительное расширение идеальных газов при неизменном давлении (p=idem) пропорционально повышению температуры

, (25)

при ; , (26)

где v – удельный объем газа при температуре t и давлении p; v₀ – удельный объем газа при температуре t₀ = 0 ⁰C; – температурный коэффициент объемного расширения идеальных газов при t₀ = 0 ⁰C, сохраняющий одно и то же значение при всех давлениях и одинаковый для всех идеальных газов.

Из сопоставления этих законов выводится уравнение состояния идеальных газов - уравнение Клапейрона (1834 г.):

для 1 кг газа ; (27)

для кг газа , (28)

где – характеристическая постоянная газа; Т – абсолютная температура газа

. (29)

Продифференцировав уравнение Клапейрона при постоянном давлении, получим: .

Отсюда

. (30)

Это значит, что характеристическая газовая постоянная (R) – это термодинамическая работа 1 кг газа в изобарном процессе (p= idem) при изменении температуры газа на один градус.

Закон Авогадро (1811 г.) – объем одного киломоля идеального газа не зависит от его природы и вполне определяется параметрами состояния газа .

Молярный объем идеального газа с использованием уравнения Клапейрона определяется из соотношения

, (31)

где Дж/(кмольК) – универсальная газовая постоянная.

Уравнения состояния для 1 кмоля и для кмолей идеального газа имеют следующий вид:

для 1 кмоля газа ; (32)

для кмолей газа . (32а)

Эти уравнения называются уравнениями Клапейрона – Менделеева.

Закон Джоуля определяет, что внутренняя энергия идеального газа зависит только от температуры

; . (33)

Реальные газы

Отсутствие теоретически обоснованного единого уравнения состояния реального газа привело к выводу большого количества эмпирических и полуэмпирических уравнений состояния, справедливых для отдельных газов в ограниченном диапазоне изменения параметров их состояния.

Чем точнее уравнение, тем больше (как правило) оно содержит индивидуальных констант. Так, в известном уравнении состояния Ван-дер-Ваальса содержится две константы, а в более точных уравнениях число констант доходит до десяти и более.

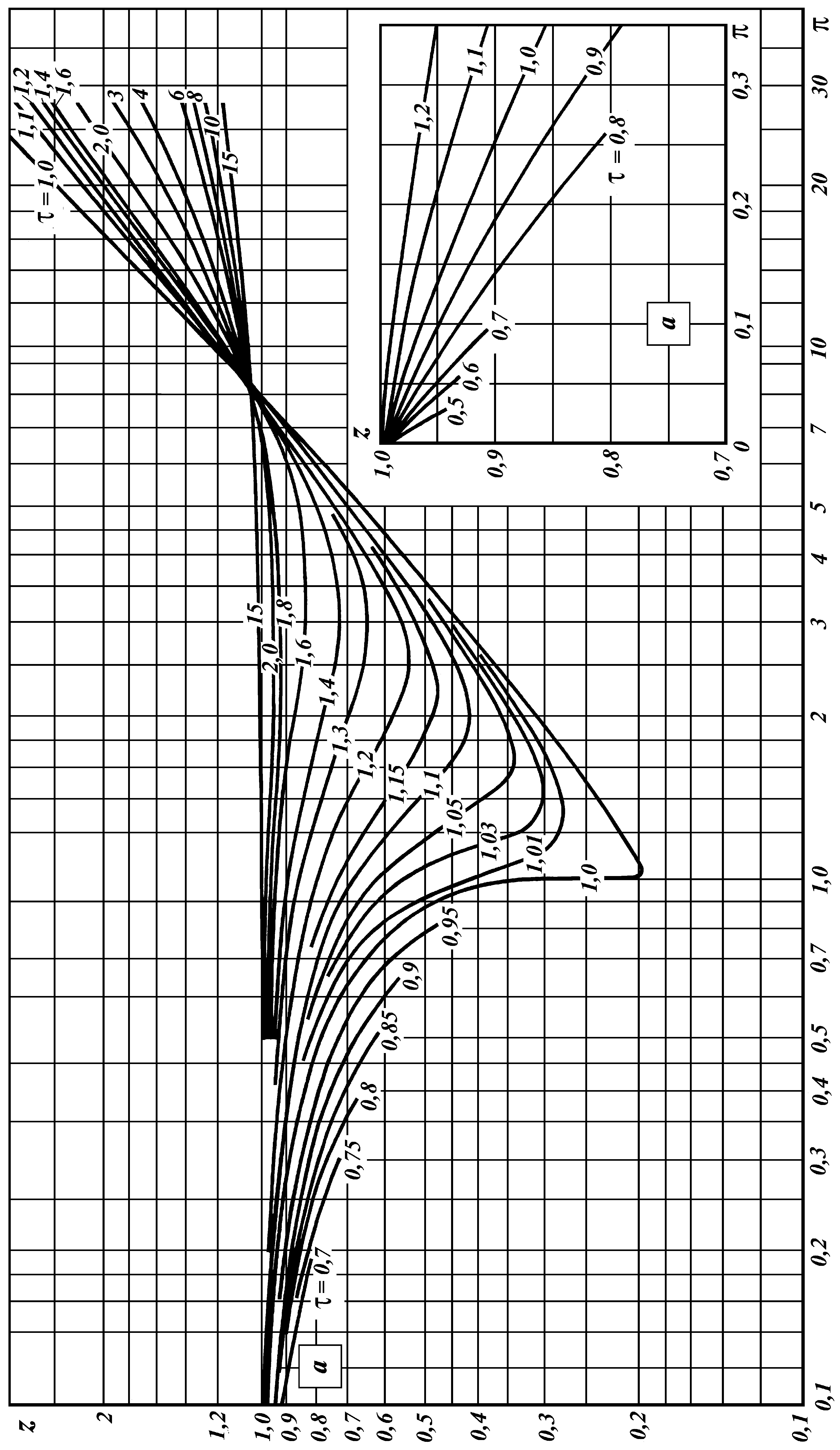
В инженерных расчетах часто пользуются уравнением состояния идеального газа с введением в него поправочного коэффициента (z), называемого коэффициентом сжимаемости

. (34)

Коэффициент сжимаемости (z) учитывает различие между идеальным и реальными газами (для идеального газа z = 1).

Коэффициент сжимаемости является функцией давления, температуры и зависит от природы газа.

Для обобщения данных по коэффициентам сжимаемости различных газов был использован принцип «соответственных» состояний, сформулированный Ван-дер-Ваальсом. Принцип «соответственных» состояний утверждает, что критическое состояние действительно является одинаковым для всех веществ.

В критической точке для всех веществ r = 0, , , . Вещества находятся в соответственных состояниях при одинаковом удалении от критической точки.

Степень удаления от критической точки определяется с помощью приведенных параметров:

• приведенного давления ;

• приведенной температуры ;

• приведенного объема .

Уравнение состояния, записанное в виде F ( ) = 0, называется приведенным уравнением состояния. Оно не содержит индивидуальных констант вещества.

Состояния вещества, в которых они имеют одинаковые и называются соответственными. Зная параметры и по данным рис. 4 определяется коэффициент сжимаемости z.