4. Циклические и итерационные алгоритмы

Методические указания

1. При подготовке к работе с данным разделом необходимо изучить такие конструкции языка: логические выражения, операторы цикла.

2. При программировании циклических алгоритмов программистами принят негласный запрет на использование меток и операторов безусловного перехода.

4.1 Некоторые типы задач, приводящие к циклическим алгоритмам

Задача. 1. Найти дальности видимости горизонта с мостиков судов, если их высоты (H) 10 ÷ 20 м. Шаг вычислений ( H) 2 метра. Радиус Земли приближенно равен 6350 км.

2. Составим блок-схему алгоритма решения задачи

Прежде чем составлять блок-схему будет полезно рассмотреть вспомогательный рисунок.

Очевидно, что дальность видимости горизонта получим из прямоугольного треугольника в виде:

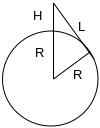
Если обозначить через Hn и Hk начальное и конечное значения высот мостиков соответственно, а через dH шаг вычислений, то можно будет записать алгоритм, с помощью которого можно рассчитать дальность видимости горизонта L для любых заданных значений.

Блок-схема будет иметь вид, показанный на рис. 4.1 .

3. Листинг

// Процедура вычисления дальности видимости горизонта

procedure TForm1.Button1Click(Sender: TObject);

const

R = 6350000;

var

H, Hn, Hk, dH : integer;

L : real;

begin

Hn := StrToInt(Edit1.Text);{Нач. высота}

Hk := StrToInt(Edit2.Text);{Конечн. высота}

dH := StrToInt(Edit3.Text);{Шаг вычислений}

H := Hn;

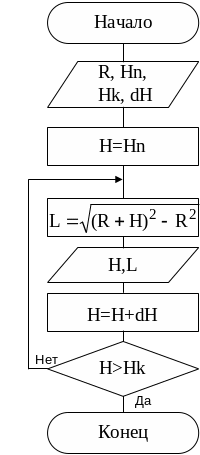
Рис. 4.1

repeat

L := sqrt(sqr(R+H)-sqr(R));

Memo1.Lines.Add('H='+IntToStr(H)+

' L='+FloatToStr(L));

H := H+dH;

until H > Hk;

end;

Варианты заданий

А) Составить блок-схему алгоритма и программу вычисления значений функций из п. 3.2 (соответствующих номеров заданий), если аргумент изменяется в диапазоне:

1. -1.1 ≤ x ≤ 1.6 с шагом h_x=0,2; 16. 1 ≤ х ≤2 с шагом h_x=0.15;

2. 0.25 ≤ x ≤ 4 с шагом h_x=0,25; 17. 0 ≤ k ≤0.7 с шагом h_k=0.12;

3. 3 ≤ x ≤ 4.25 с шагом h_x=0,25; 18. 1 ≤ х ≤2.7 с шагом h_x=0.1;

4. 0.25 ≤ x ≤ 3 с шагом h_x=0,30; 19. 2 ≤ х ≤3 с шагом h_x=0.01;

5. 0 ≤ m ≤ 10 с шагом h_m=1; 20. 2 ≤ х ≤ 2.5 с шагом h_x=0.01.

6. 0.25 ≤x <3 с шагом h_x=0,25; 21. 1.6 ≤ х ≤ 2.2 с шагом h_x=0.1;

7. 0.45 ≤ x ≤4 с шагом h_x=0,25; 22. 1.1 ≤ х ≤ 1.5 с шагом h_x=0.05;

8. -1 ≤ x≤ 3.5 с шагом h_x=0,5; 23. 1 ≤ х ≤ 1.5 с шагом h_x=0.07;

9 . -4 ≤ k ≤ 8 с шагом h_k=1; 24. 1.7 ≤ х ≤ 2.5 с шагом h_x=0.1;

10.-5≤ x ≤ 5 с шагом h_x=0,5; 25. 1.3 ≤ х ≤ 2.9 с шагом h_x=0.1;

11. 2≤ x ≤ 9 с шагом h_x=0,85; 26. 2.9 ≤ х ≤ 3.1 с шагом h_x=0.05;

12. 1 ≤ k ≤ 5 с шагом h_k=1,25; 27. 1.6 ≤ х ≤ 2.7 с шагом h_x=0.1;

13. 12≤ x ≤ 20 с шагом h_x=2; 28. 1.7 ≤ х ≤ 2.1 с шагом h_x=0.07;

14. 1 ≤ m ≤ 5 с шагом h_m=1; 29. 1.1 ≤ х ≤ 2.2 с шагом h_x=0.1;

15. 1 ≤ n ≤ 3 с шагом h_n=1; 30. 1.4 ≤ х ≤ 2.4 с шагом h_x=0.15.

Б) Составить блок-схемы алгоритмов и программы решения следующих задач. Во всех задачах предусмотреть вывод результатов.

1. Составить таблицу перевода температуры из градусов по шкале Цельсия (С) в градусы по шкале Фаренгейта (F) для значений от 15 C до 100C c шагом 5С. (Перевод осуществляется по формуле F=1.8 C+32.)

2. Составить таблицу соответствия между весом в фунтах и весом в кг для значений от 1 до 10 фунтов с шагом 2 фунта (1 фунт = 400 г).

3. Составить таблицу перевода расстояний из дюймов в сантиметры (1 дюйм = 2.54 см) для значений от 1 до 20 дюймов с шагом 2 .

4. Составить таблицу умножения для числа 12.

5. Вычислить сумму квадратов первых 7 натуральных чисел.

6. Составить таблицу значений функции y=x³ при изменении x от 2 до 12 с шагом 2.

7. Вычислить произведение первых 10 натуральных чисел.

8. Вычислить : а) используя операцию возведения в степень; б) не используя операцию возведения в степень.

9. Вычислить , не используя операцию возведения в степень.

10. Числа Фибоначчи – это последовательность u1,u2,u3,. . . , образованная по закону: каждый последующий член последовательности равен сумме двух предыдущих ее членов. При этом а₀=0, а₁=1. Вычислить n-ное число Фибоначчи.

11. Плотность воздуха убывает с высотой по закону . Считая, что =1.29 кг/м³ , z =1/25*10^-4 1/м, составить таблицу зависимости плотности воздуха от высоты для значений от 0 до 1000 м с шагом 100 м.

12. Определить наибольшее число, факториал которого не превосходит 10⁵.

13. Около стены наклонно стоит палка длиной x. Один ее конец находится на

расстоянии y от стены. Определить значение угла  между палкой и стеной

для значений x = 4.5 м и y, изменяющегося от 2 до 3 м с шагом 0.2 м.

14. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Считая, что первоначально в замкнутом объеме находится 10 клеток, определить, через какое время в этом объеме будет находиться 10⁵ клеток.

15. Концентрация хлорной извести в бассейне объемом V м³ составляет 10 г/л. Через одну трубу в бассейн вливают чистую воду с объемной скоростью Q м³/час, через другую трубу вода с той же скоростью выливается. При условии идеального перемешивания концентрация хлорной извести изменяется по закону где t – время, - начальная концентрация. Определить, через какое время концентрация хлорной извести достигнет безопасной для человека величины 0.1 г/л. Задачу решить при Q =160 м³/час, V = 10000 л, = 10 г/л.

16. Вычислить n-й член последовательности, образованной дробями: 1/1, 2/1, 3/2, …, то есть числитель (знаменатель) следующего члена получают сложением числителей (знаменателей) двух предыдущих членов. Числители первых двух членов равны 1 и 2, знаменатели равны 1. Выполнить при n=5.

17.Селекционер вывел новый сорт зерновой культуры и снял с опытной делянки k кг семян. Посеяв 1 кг семян, можно за сезон собрать р кг семян. Через сколько лет селекционер сможет засеять новой культурой поле площадью S га, если норма высева n кг/га?

18. По древней легенде мудрец, который изобрел шахматы, потребовал от персидского шаха такое количество пшеницы, чтобы им можно было покрыть шахматную доску, положив на первую клетку одно зерно, на вторую – 2, на третью – 4 и т.д., то есть, помещая на каждую следующую клетку в два раза больше зерен, чем на предыдущую. Какое количество зерна необходимо для покрытия доски? (Считать, что в одном грамме 15 зерен.)

19. Получить таблицу значений функции при изменении x от 0 до 1, разбивая отрезок [0,1] на 10 частей. Для каждого значения x суммирование прекращать, когда очередной член суммы по абсолютной величине станет меньше или равен 10^-4.

20. Известно, что в 1 г живой клетчатки (например, дерева) содержится

7.5*10¹⁰ ядер радиоактивного углерода. После гибели организма радиоактивные ядра начинают распадаться и их концентрация уменьшается по закону , где - начальная концентрация, - период полураспада (для радиоактивного углерода равен 5570 годам).

Построить таблицу зависимости концентрации радиоактивных ядер от времени для интервала времени от 0 до 6000 лет с шагом 500 лет, считая за 0 момент гибели организма (дерева).