Задание к лабораторной работе №2.

1. По заданному шаблону схемы (рис.6) и номеру варианта построить свой вариант схемы. Для этого необходимо представить номер варианта в двоичном виде. Выбор типов вентилей:

   • вентиль = «ИЛИ» для чётных вариантов, «И» - для нечётных;

   • типы вентилей - определяются по двоичному разложению номера варианта , где

2. Построить полное множество неисправностей для заданной схемы. Для работы выбираются неисправности с номером , где - номер варианта.

3. Для заданной схемы (пункт 1) и выбранной неисправности (пункт 2) построить тест методом существенного пути.

Контрольные вопросы к лабораторной работе №2.

1. Дайте определение проявления и транспортировки неисправностей.

2. Зависят ли проявление и транспортировка от типа рассматриваемой неисправности?

3. Зависят ли проявление и транспортировка неисправности от типа вентиля, которому принадлежит линия с неисправностью.

4. Напишите условия транспортировки для следующих случаев:

• вентиль 3И-НЕ, неисправен первый вход;

• вентиль 3ИЛИ-НЕ, неисправен третий вход;

• вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ, неисправен первый вход.

5. В чём заключается метод существенного пути построения тестов? Какие цели ставятся в фазах 1 и 2 алгоритма?

Лабораторная работа №3. Метод построения тестов с помощью различающей функции.

Определение. Различающей называется функция , где описывает поведение функции в присутствии неисправности либо .

П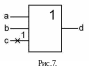 ример 1.а) Построить тест с помощью различающей функции для неисправности на рис.7.

. Таким образом, .

П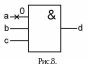 ример 1.б) Построить тест с помощью различающей функции для неисправности на рис.8.

, , , т.е. .

П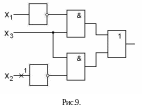 ример 2а) Построить тест с помощью различающей функции для заданной булевой функции и неисправности .

Построим комбинационную схему, реализующую заданную функцию – рис.9. Построим различающую функцию:

. Для получения тестового набора приравняем к 1, тогда , или .

Пример 2.б) Построить тест с помощью различающей функции для заданной булевой функции и неисправности .

Построим различающую функцию:

= .

Приравняем к 1, тогда: 1) , , ; 2) , , .

Получаем тест: .

П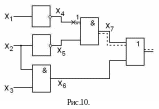 ример 2.в) Построить тест с помощью различающей функции для заданной булевой функции и неисправности .

Построим комбинационную схему, реализующую заданную функцию – рис.10. Построим различающую функцию:

, откуда получаем , .

П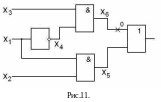 ример 2.г) Построить тест с помощью различающей функции для заданной булевой функции и неисправности .

Построим комбинационную схему, реализующую заданную функцию – рис.11. Построим различающую функцию:

, откуда, приравнивая к 1, получим , или .

Задание. Построить тест с помощью различающей функции для схемы и неисправностей из предыдущего задания.

Лабораторная работа №4. Булевы производные.

Определение. Булевой производной булевой функции по переменной называется .

Пример 1.а) Построить по определению булевы производные по всем переменным для функции .

.

.

.

Пример 2.б) Построить по правилу дифференцирования булеву производную.

.

.

.

Пример 3а) Построить тест для заданной неисправности методом булевой производной (БП): , .

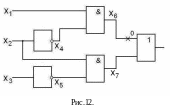
Для наглядности построим логическую схему, реализующую данную функцию (рис.12). Различающая функция имеет вид:

, или ,

, тогда имеем

.

Приравнивая к 0, получаем , , , или .

Пример 3а) Построить тест для заданной неисправности методом булевой производной (БП): , .

Построим различающую функцию:

,

; ; .

Тогда

или . Приравнивая к 1, получаем , , , или .

Пример 3а) Построить тест для заданной неисправности методом булевой производной (БП): , .

Поступаем аналогичным образом:

.

,

, .

….

Задание. Построить тест методом булевой производной для схемы и неисправностей из предыдущего задания.