Задача 11. Решить следующие линейные неоднородные уравнения с правой частью специального вида методом подбора частного решения по виду правой части.

1.	.
2.	.
3.	.
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.

Задача 12. Метод вариации произвольных постоянных, метод Лагранжа.

Рассмотрим метод вариации произвольных постоянных для уравнения второго порядка

(1)

Если известна фундаментальная система решений соответствующего однородного уравнения

, (2),

то общее решение неоднородного уравнения (1) может быть найдено методом вариации постоянных (метод Лагранжа).

Общее решение уравнения (2) имеет вид

, (3)

где – фундаментальная система решений (ф.с.р.),

– произвольные постоянные.

Решение уравнения (1) будем находить в виде

, (4)

где – некоторые пока неизвестные функции от х. Для их определения получаем систему

(5)

Решая (5) относительно , получим

(6)

– определитель Вронского.

, т. к. – ф. с. р.

Из (6) находим

,

где – постоянные интегрирования.

Пример 18. Решить уравнение .

Решение.

Соответствующее однородное уравнение будет .

Его характеристическое уравнение и общее решение имеет вид .

Общее решение исходного уравнения имеем в виде

(*)

– ф. с. р.

– неизвестные функции от .

Для их нахождения составим систему

Решаем эту систему относительно :

.

Интегрируя, находим

.

Подставляя выражения в (*), получаем общее решение искомого уравнения

.

Здесь – частное решение исходного уравнения.

Упражнения. Решить уравнения.

1) . Ответ: .

2) . Ответ: .

3) . Ответ: .

4) . Ответ: ,

или .

Решить методом вариации произвольных постоянных следующие уравнения:

1. .	4. .
2. .	5. .
3. .	6. .
7. .	19. .
8. .	20. .
9. .	21. .
10. .	22. .
11. .	23. .
12. .	24. .
13. .	25. .
14. .	26. .
15. .	27. .
16. .	28. .
17. .	29. .
18. .	30. .

Рассмотрим задачу , (1)

, (2)

, (3)

где – ф.с.р. Если – нормированная ф.с.р., т. е , то решение задачи Коши (1), (2) запишется в виде

. (4)

Пример 19. Решить методом Коши

.

Решение.

– корни х.у., – ф.с.р.

Найдем нормированную ф.с.р.:

будем находить в виде линейной комбинации решений и :

а) ,

б)

.

Вычислим интеграл:

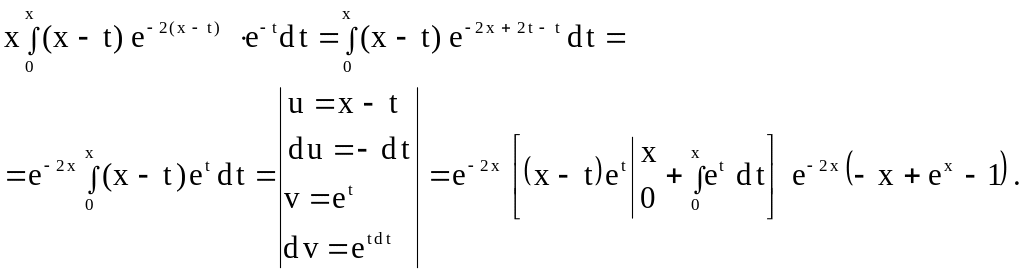
Подставим в решение .