Пример 3.

Решить уравнение .

Решение. Запишем уравнение в виде , разделив на обе части уравнения. Сделаем замену . Тогда , . Получим или .

Разделяя переменные, будем иметь .

Отсюда интегрированием находим

или

, так как , то обозначая , получим

. Заменяя на , будем иметь общий интеграл

, отсюда - общее решение.

Ответ: .

Упражнения. Решить уравнения

1. . Ответ: .

2. . Ответ: .

3. . Ответ: .

4. . Соберем коэффициенты при . Ответ: .

Решить однородные дифференциальные уравнения.

1.	.
2.	.
3.	.
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.

Задача 3. Линейные дифференциальные уравнения первого порядка.

Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной. Оно имеет вид

(1)

где - заданные функции от , непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если , то уравнение (1) называется линейным однородным. Оно является уравнением с разделяющимися переменным и имеет общее решение

.

Общее решение неоднородного уравнения можно найти следующими способами:

1) методом вариации произвольной постоянной, который состоит в том, что

решение уравнения (1) находится в виде

, где - новая неизвестная функция.

2) уравнение (1) может быть проинтегрирован с помощью подстановки , где - неизвестные функции от .

3) решение уравнения (1) можно найти еще и по формуле

.

Замечание. Может оказаться, что дифференциальное уравнение линейно относительно как функции от . Нормальный вид (коэффициент при равен 1) такого уравнения

( )

Пример 4.

Решить уравнение .

Решение. Вид уравнения нормальный

.

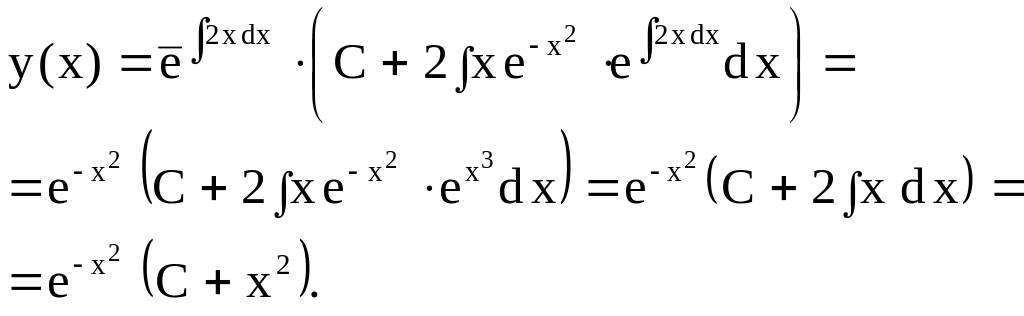
Ответ: .

Упражнения. Решить уравнения

1. . Ответ: .

2. .

Приводим к виду , и решаем по формуле, которая была выведена на лекциях ( повторить, потому, что вывод спрашивают !) . Ответ: .

3. . Ответ: .

4. . Ответ: .

Уравнение линейное относительно функции . Приводим его к виду

или .

Решить линейные дифференциальные уравнения первого порядка:

1.	.
2.	.
3.	; .
4.	.
5.	.
6.	.
7.	.
8.	.
9.	.
10.	.
11.	.
12.	.
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.
22.	.
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.