1.6. Расчет элементов плиты по первой группе предельных состояний

1.6.1 Расчет верхней обшивки каркасной панели

13. Напряжение в верхней обшивке:

< f_с.o.d. = 27,45 МПа – напряжения в элементах каркасных плит не превышают расчетного сопротивления сжатию листового асбестоцемента.

1.6.2 Расчёт нижней обшивки каркасной панели

14. Напряжение в нижней обшивке определяем по формуле:

< f_t.o.d. = 7,65 МПа – напряжения в нижней обшивке не превышают расчетного сопротивления растяжению листового асбестоцемента.

1.6.3 Расчёт рёбер каркаса панелей

Определение геометрических характеристик сечения с учётом податливости (m=0,22)

15. Определение нового положения нейтральной оси с учетом податливости соединения обшивок с каркасом:

16. Моменты инерции поперечного сечения относительно новой нейтральной оси у_w, положение которой определяется с учетом податливости соединений:

- ребра:

- верхней обшивки:

- нижней обшивки:

17. Определяем коэффициент β:

18. Напряжения изгиба в каркасе определяем по формуле:

< f_m.d = 16,85 МПа – напряжения в элементах каркасных плит не превышают расчетного сопротивления изгибу древесины.

19. Напряжения скалывания в каркасе при изгибе определяем по формуле:

,

где - статический момент сдвигаемой части поперечного сечения конструкции, приведенный к древесине, относительно нейтральной оси :

- момент инерции всего расчетного сечения, приведенного к древесине, относительно с учетом податливости (m₀ = 0,22):

Так как < f_v.0.d = 1,73 МПа - напряжения скалывания в ребре не превышают расчетного сопротивления скалыванию вдоль волокон древесины.

1.7. Расчет элементов плиты по второй группе предельных состояний

Проверку производим по формуле

;

где - прогиб плиты без учета деформаций сдвига; U_lim / l – максимально допустимый предельный прогиб плиты, определяемый по /1, табл.4.1/. При =5029,2 мм

, - проверка не выполняется.

1.8. Расчет элементов соединений обшивок с каркасом

Расчет элементов соединения обшивок с каркасом проводим, исходя из выполнения неравенства:

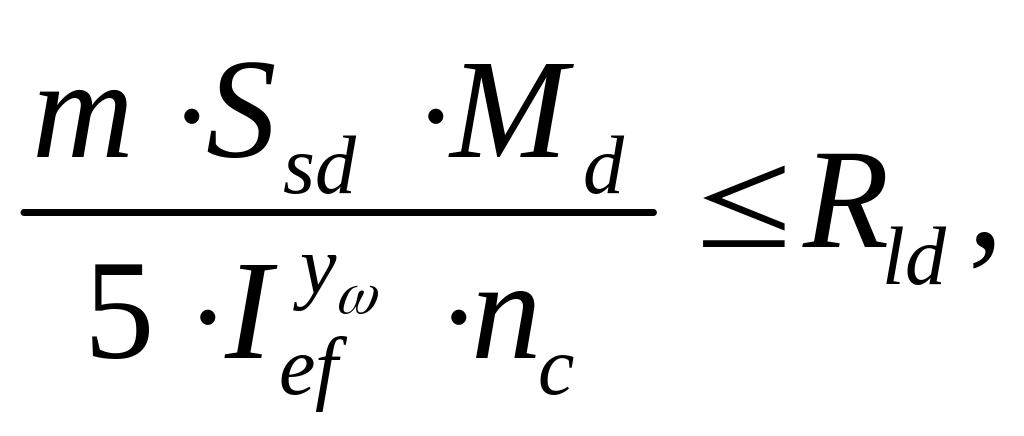
где – максимальный расчетный изгибающий момент на рассматриваемом участке с однозначной эпюрой поперечных сил;

= 14 – число принимаемых срезов элементов соединения в каждом шве на рассматриваемом участке с однозначной эпюрой поперечных сил;

–статический момент сдвигаемой части поперечного сечения конструкции относительно нейтральной оси;

– момент инерции всего расчетного сечения, приведенного к древесине, относительно y_w с учетом податливости (при максимальном значении m=0,79):

Расчетная несущая способность одного шурупа:

где f_сm = 27,45 МПа – расчетные сопротивления смятию обшивки;

f_h.2.d = 2,5·1,2·1,2·1=3,6 МПа – расчетное сопротивление смятию древесины /1, табл.4.2/ с учетом коэффициентов k_mod·k_x·k_t;

f_n.d – расчетное сопротивление изгибу нагеля /1,табл.4.3/;

t₁ = 10 мм – толщина обшивки;

t₂ = 100 мм – толщина древесины каркаса;

d = 4 мм – диаметр шурупа;

β_n– коэффициент, зависящий от отношения толщины более тонкого элемента к диаметру нагеля;

k_α – коэффициент, учитывающий угол между силой и направлением волокон /1,табл. 4.4 /.

где k_n = 0,0632 – коэффициент, зависящий от типа нагеля /1,табл.4.3/.

Значение коэффициента _n не должно превышать значения _n,max = 0,7746 /1, табл.4.3/.

Проверяем условие:

Условия прочности выполняются.