
- •Законы распределения случайных величин. Статистический анализ рядов распределения
- •Тема. Законы распределения случайных величин. Статистический анализ рядов распределения
- •Основные теоретические сведения
- •Случайная величина и ее распределение. Функция распределения и плотность вероятности.
- •Теоретическое распределение дискретной случайной величины
- •Эмпирическое распределение дискретной случайной величины
- •Эмпирическое распределение случайной величины непрерывного типа
- •1.2. Законы распределения случайных величин
- •1.2.1. Закон биноминального распределения.
- •1.2.2. Закон редких событий (Пуассона)
- •1.2.3. Закон нормального распределения.
- •1.2.4. Закон равной вероятности.
- •1.2.5. Закон распределения эксцентриситета (Релея).
- •1.2.6. Закон распределения модуля разности.
- •Значения для величин
- •Значения для величин
- •1.2.7. Закон экспоненциального распределения
- •1.2.8. Закон распределения Вейбулла
- •1.2.9. Закон логарифмического нормального распределения
- •Методические рекомендации по выполнению анализа статистических данных
- •3. Задание
- •Варианты заданий по п. 2
- •Варианты заданий по п.1
- •Результаты проверки качества деталей
- •Результаты испытаний надежности изделий
- •Результаты исследования стойкости резцов
- •Результаты исследования стойкости сверл
- •Отклонения от номинального размера диаметра валиков в мм.
- •Результаты исследования стойкости плашек м10 × 1,5
- •Величина конусности роликов в мкм
- •Величина овальности валиков в мкм
- •Отклонения от номинального размера диаметра отверстия втулок в мм.
- •4. Порядок выполнения работы
- •5. Пример выполнения и оформления отчета Тема. Законы распределения случайных величин. Статистический анализ рядов распределения
- •5.1. Задание
- •5.2. Выполнение задания по п. 1.
- •5.3. Выполнение задания по п. 2.
- •Эмпирическое распределение х
- •6. Содержание отчета
- •Контрольные вопросы
- •Литература
1.2.5. Закон распределения эксцентриситета (Релея).
Закон распределения эксцентриситета (закон Релея), имеет место при отклонениях эксцентриситета осей или биения поверхностей деталей, которые являются непрерывными случайными величинами. Этот закон однопараметрический и дифференциальная функция распределения его имеет выражение:
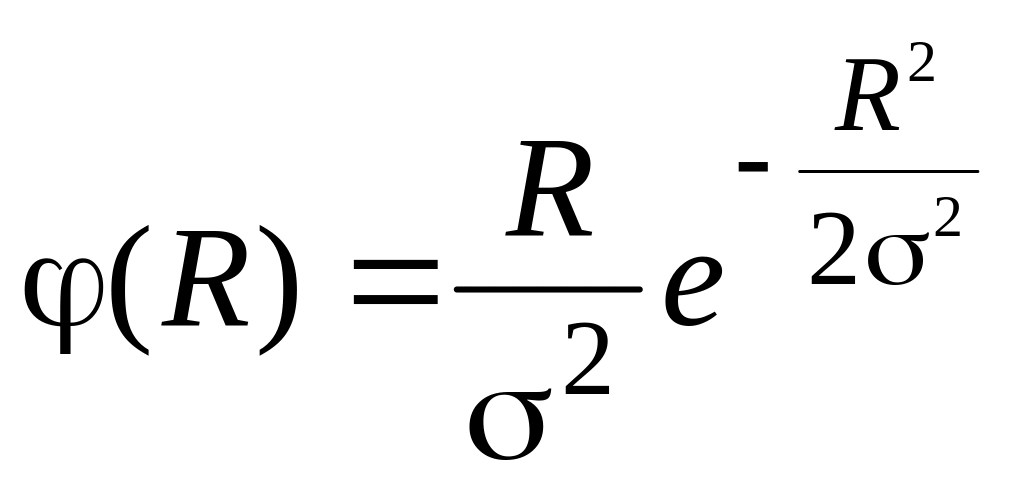 ,
(7)
,
(7)
где R
— переменная величина эксцентриситета
или биения,
![]() ;
;
х и у — координаты точки конца R; σ - среднее квадратическое отклонение значений координат х и у, имеющих одинаковое распределение; поэтому
σ = σх = σу.
Интегральный закон распределения эксцентриситета записывается в виде
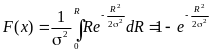 .
(8)
.
(8)
1.2.6. Закон распределения модуля разности.
Если две случайные
величины х1
и
х2
каждая в отдельности имеют нормальное
распределение с параметрами
![]() и
и
![]() и
и
![]() ,
то модуль разности этих величин
,
то модуль разности этих величин
![]()
имеет распределение, которое носит название закона распределения модуля разности. Этому закону распределения, например, часто подчиняются погрешности взаимно расположенных поверхностей и осей, а также погрешности формы деталей: овальность, конусность.
Дифференциальная функция распределения случайной величины r выражается следующим уравнением:
 ,
(9)
,
(9)
где
![]() и σ0
являются параметрами распределения
модуля разности r.
и σ0
являются параметрами распределения
модуля разности r.
Интегральная функция распределения модуля разности r имеет вид:
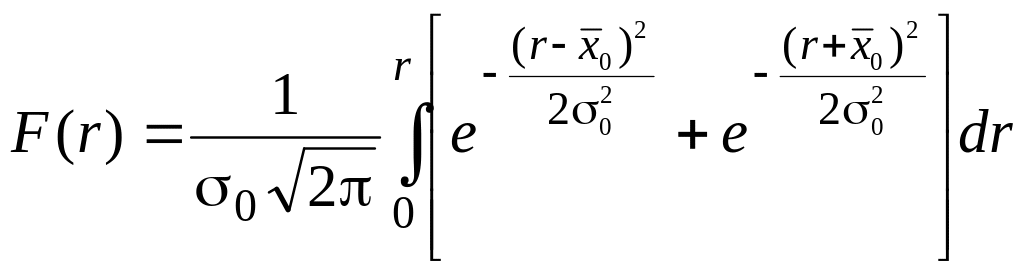 (10)
(10)
Произведя замену переменных в уравнениях (9) и (10):
![]() ,
,
![]() ,
,
![]() ,
,
получим следующие выражения
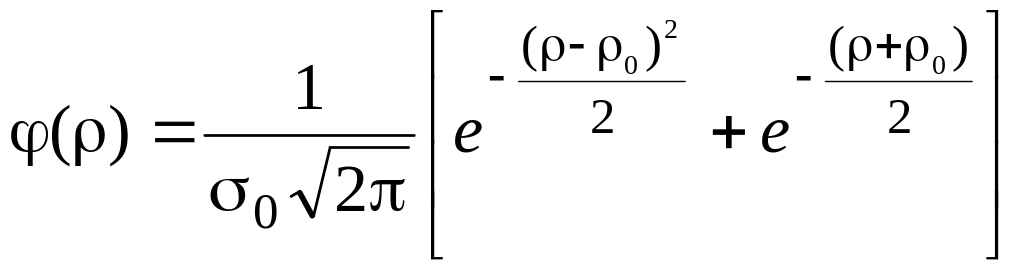 ;
;
 .
.
Между
σr,
![]() и ρ0
существует определенная зависимость,
которая определяется через нормированное
,
обозначаемое λ0:
и ρ0
существует определенная зависимость,
которая определяется через нормированное
,
обозначаемое λ0:
![]() .
.
Среднее значение и среднее квадратическое отклонение σr случайной величины r вычисляются по экспериментальным данным. По полученному значению λ0 определяют ρ0 при помощи табл. 4, а по ρ0 определяют σρ по табл. 5.
3ная ρ0
и σρ,
можно определить параметры распределения
σ0 и
![]() по формулам
по формулам![]() ;
;
![]() .
.
Таблица 4
Значения для величин
|
|
|
|
|
|
|
|
|
|
1,3236 |
0,00 |
1,360 |
0,65 |
1,59 |
1,28 |
1,90 |
1,76 |
2,43 |
2,39 |
1,324 |
0,19 |
1,370 |
0,70 |
1,61 |
1,32 |
1,93 |
1,80 |
2,47 |
2,44 |
1,325 |
0,27 |
1,380 |
0,75 |
1,63 |
1,35 |
1,96 |
1,84 |
2,51 |
2,48 |
1,326 |
0,31 |
1,390 |
0,79 |
1,65 |
1,39 |
1,99 |
1,88 |
2,55 |
2,52 |
1,327 |
0,34 |
1,400 |
0,82 |
1,67 |
1,42 |
2,03 |
1,93 |
2,59 |
2,56 |
1,329 |
0,38 |
1,410 |
0,86 |
1,69 |
1,45 |
2,07 |
1,98 |
2,63 |
2,61 |
1,331 |
0,41 |
1,430 |
0,92 |
1,71 |
1,48 |
2,11 |
2,02 |
2,67 |
2,65 |
1,333 |
0,44 |
1,450 |
0,97 |
1,73 |
1,51 |
2,15 |
2,07 |
2,71 |
2,69 |
1,335 |
0,47 |
1,470 |
1,03 |
0,75 |
1,54 |
2,19 |
2,12 |
2,76 |
2,74 |
1,337 |
0,49 |
1,490 |
1,07 |
1,77 |
1,57 |
2,23 |
2,17 |
2,81 |
2,80 |
1,339 |
0,51 |
1,510 |
1,12 |
1,79 |
1,60 |
2,27 |
2,21 |
2,86 |
2,85 |
1,342 |
0,53 |
1,530 |
1,16 |
1,81 |
1,63 |
2,31 |
2,26 |
2,91 |
2,90 |
1,346 |
0,57 |
1,550 |
1,20 |
1,84 |
1,68 |
2,35 |
2,30 |
2,96 |
2,95 |
1,350 |
0,59 |
1,570 |
1,24 |
1,87 |
1,72 |
2,39 |
2,35 |
3,00 |
2,99 |
Таблица 5
