1.2. Законы распределения случайных величин

1.2.1. Закон биноминального распределения.

Закон биноминального распределения используется при оценке качества и надежности изделий.

Закон биномиального распределения формулируется в виде: если вероятность события А постоянна в серии последовательных независимых испытаний и равна p, то вероятность появления события А ровно k раз в n испытаниях будет равна

(1)

Это уравнение определяет собой распределение вероятностей случайного числа k, которое называется биномиальным.

Параметры закона: n – число испытаний; p - вероятность появления события А заданное число k раз.

Математическое ожидание Мk и дисперсия биномиального распределения равны:

Мk = пp; = пpk.

Вероятность того, что случайная величина k не превысит заданного значения k΄, находится по формуле

1.2.2. Закон редких событий (Пуассона)

Если вероятность р события А очень мала (p ≤ 0,1), а число испытаний велико, то вероятность того, что событие А наступит k раз в п испытаниях, будет равна

(2)

где а = пp = Мk — математическое ожидание числа k.

Уравнение (2) определяет собой распределение редких событий, или распределение Пуассона.

Интегральная функция распределения определяется по формуле

.

Теоретические частоты распределения вычисляются по формуле

где - среднее значение чисел k_i появления события A в i-й партии изделий (i = 1, 2, 3,…,n).

Распределение Пуассона имеет только один параметр a = np = Мk. Для этого распределения дисперсия численно равна математическому ожиданию: = Мk. Поэтому, когда в распределении дискретной случайной величины и σ² мало отличаются друг от друга по своим численным значениям, то можно уверенно считать, что данное распределение подчиняется закону редких событий.

Закон редких событий имеет практическое применение в машиностроении для выборочного контроля готовой продукции, когда по техническим условиям в принимаемой партии продукции допускается некоторый процент брака (обычно небольшой) и поэтому обычно p << 0,1, а объем выборки n берут таким, чтобы было np << 4.

1.2.3. Закон нормального распределения.

Закон нормального распределения находит большое применение в различных отраслях техники. Этому закону подчиняются, многие непрерывные случайные величины, встречающиеся в технике, например ошибки измерения, высота микронеровностей на обработанной поверхности и многие другие.

Плотность вероятности случайной величины непрерывного типа, подчиняющейся закону нормального распределения, имеет следующее выражение:

(3)

где х- переменная случайная величина; φ(х)- плотность вероятности; σ- среднее квадратическое отклонение случайной величины х от ; - среднее значение (математическое ожидание) величины х;

Интегральный закон нормального распределения записывается в виде:

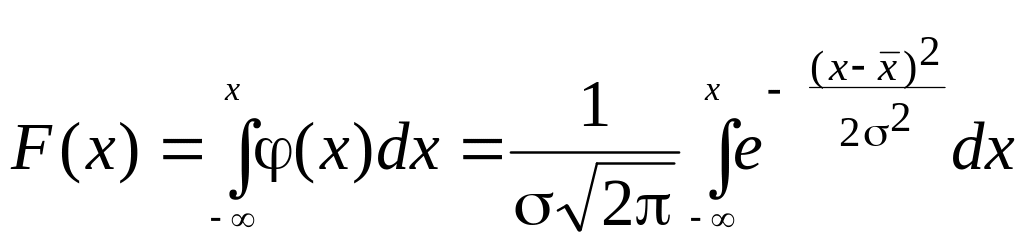. (4)

1.2.4. Закон равной вероятности.

Если непрерывная случайная величина х при испытаниях принимает все значения интервала (a, b) с одинаковой плотностью вероятности, то распределение плотности вероятности графически будет выражаться в виде прямоугольника с основанием ab и высотой φ(х) = const. Такой закон распределения непрерывной случайной величины называется законом равной вероятности, а само распределение - равномерным.

Уравнение дифференциальной функции распределения по закону равной вероятности имеет вид:

(5)

Закон равной вероятности имеет два параметра: Мх  и σ², которые равны: , .

Интегральная функция равномерного распределения выражается следующим уравнением для (а < х < b):

. (6)

Законом равной вероятности описывается распределение показателей точности обработки, на величину которых оказывает влияние доминирующий фактор, изменяющийся во времени (износ инструмента, изменение температуры и т. п.)