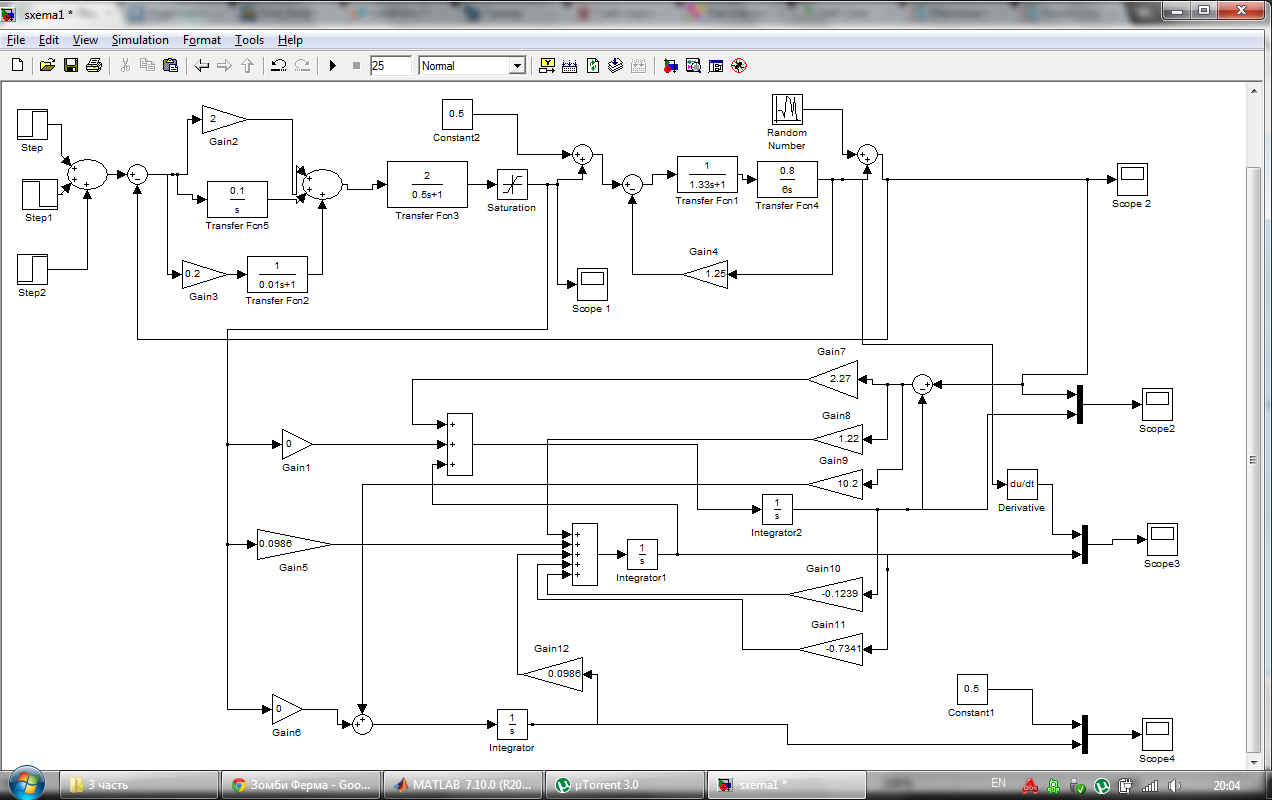
3.Построение наблюдателя

Разработка наблюдателя состояния:

f

u

y

Передаточная функция объекта:

W(s)= =

Дифференциальное уравнение объекта:

1.0621y’’+5,9213y’+y=0.9958(u+f)

Измеряется у. Введем координаты состояния:

_{Тогда уравнения в пространстве состояний:}

Y(t)=y(t); у=

_{Так как f меняется медленно, то предположим, что f=const.}

А= ; В= ; С=

Матрица наблюдаемости:

M=

Динамическая система называется наблюдаемой, если найдется такой интервал [tн;tк], что по результатам измерения вектора Y(t) можно однозначно восстановить значения вектора координат состояния Х(t).

Ранг матрицы наблюдаемости очевидно равен трем, значит система наблюдаема.

_{Матрица коррекции:}

Вычислим детерминант матрицы :

Для того, чтобы переходный процесс в наблюдателе длился tп=6с, выберем все собственные числа . Уравнение, в котором полином 3-го порядка относительно λ имеет все корни равные -0.5, можно записать в виде:

_{Приравнивая коэффициенты при одинаковых степенях λ, получаем}

Отсюда:

_{Выбранные таким образом коэффициенты матрицы коррекции К обеспечат сходимость оценок координат состояния наблюдателя к истинным значениям примерно за 6с.}

Далее предлагается рассмотреть систему с наблюдателем, построенную в MatLab и графики изменения во времени истинных значений координат состояния и результатов их наблюдения. При задании нулевых начальных условий в блоке Integrator в строке Initial Condition ввели начальные условия в соответствии с заданием.

В качестве помехи f=const=0.2 использовали блок Constant.

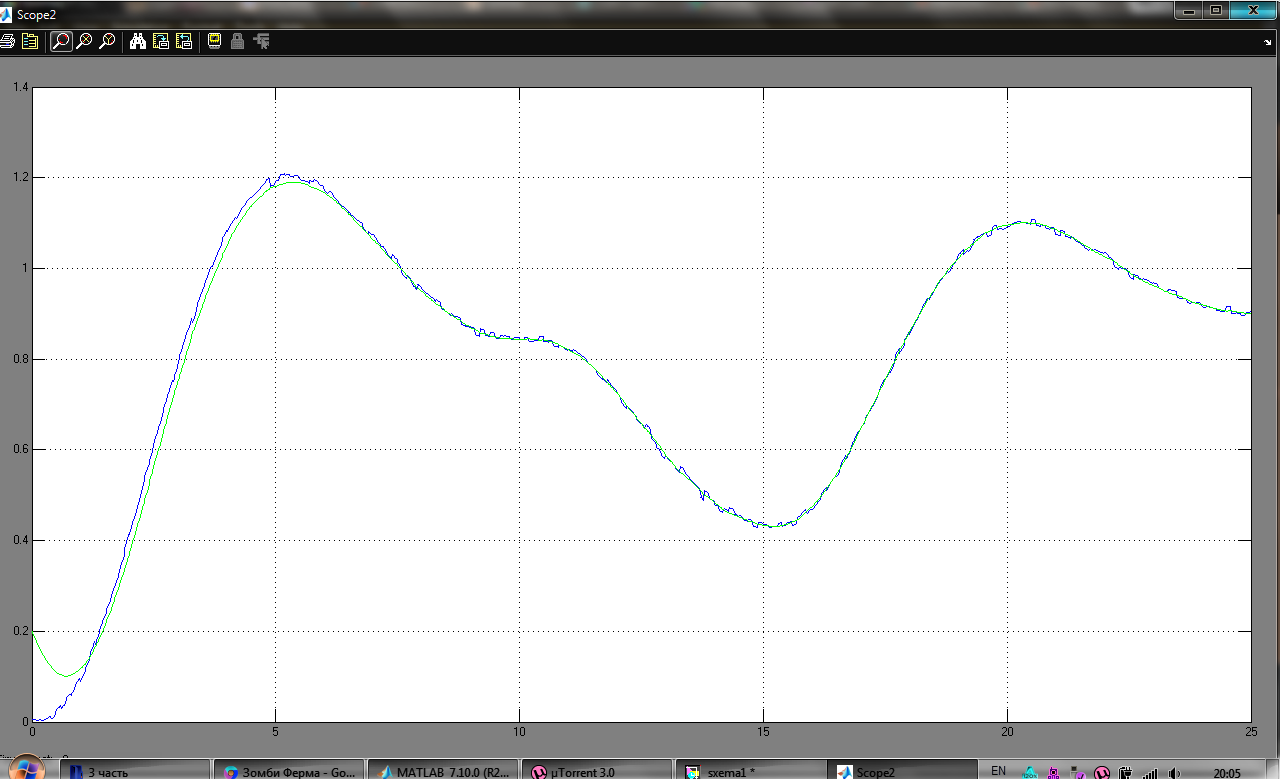
График, показывающий у при движении объекта из нулевых начальных условий и у(0) при движении наблюдателя из у(0)=-0,2

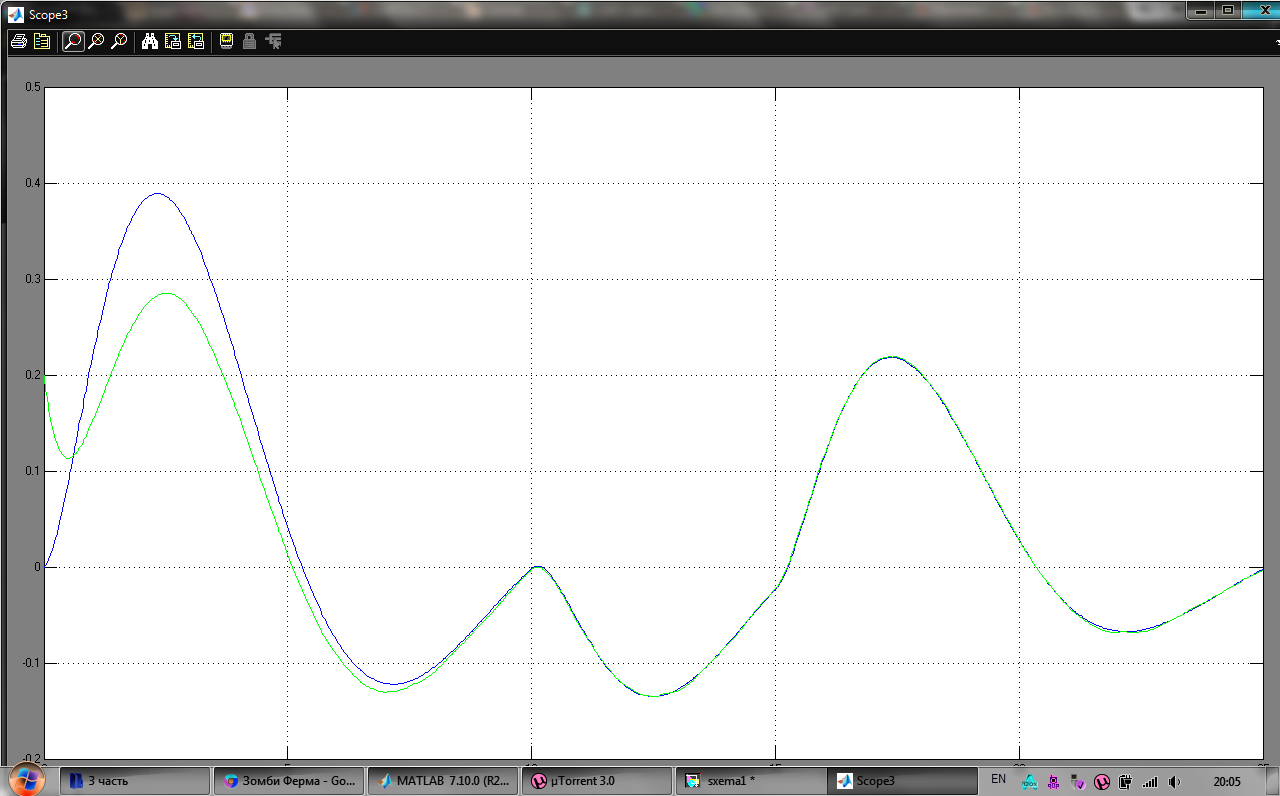
График, показывающий у´ при движении объекта из нулевых начальных условий и у´ (0) при движении наблюдателя из у´ (0)=0,1

График, показывающий f при движении объекта и f=const=0,2 при движении наблюдателя

Заключение

Приобрели практические навыки в моделировании на ЭВМ динамических систем управления, в идентификации объектов по данным нормальной эксплуатации в контуре управления, а также в построении и моделировании работы наблюдателя координат состояния.

Список литературы

1. Моделирование систем: метод. Указания к выполнению курсовой работы/ В.А. Кривоносов. – Старый Оскол, 2003. – 22с.