2.1. Арифметика целых чисел

В арифметике целых чисел мы используем множество целых чисел и несколько операций. Вы знакомы с этим множеством и соответствующими операциями, но они рассмотрены здесь, чтобы объяснить потом основы действий со сравнениями по модулю m.

Множество целых чисел

Множество целых чисел, обозначенных Z, содержит все числа (без дробей) от минус бесконечности до плюс бесконечности

Бинарные операции

В криптографии нас интересует три бинарных операции в приложении к множеству целых чисел. Бинарные операции имеют два входа и один выход. Для целых чисел определены три общих бинарных операции — сложение, вычитание и умножение. Каждая из этих операций имеет два входа (a и b) и выход (c). Два входа принимают числа из множества целых чисел; выход выводит результат операции — число из множества целых чисел.

Обращаем внимание, что деление не относится к этой категории операций, потому что мы скоро убедимся, что этой операции нужны два выхода вместо одного.

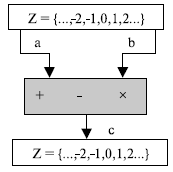
Рис. 2.2.  Три бинарных операции для множества целых чисел

Пример 2.1

Следующие примеры показывают результаты трех двоичных операций на множестве двух целых чисел. Поскольку каждый вход может быть или положителен или отрицателен, мы имеем четыре случая для каждой операции.

Сложение 5+9=14 (-5)+9=4 5+(-9)=-4 (-5)+(-9)=-14

Вычитание 5-9=-4 (-5)-9=-14 5 - (-9)=14 (-5)- (-9)=+4

Умножение 5 × 9=45 (-5) × 9=-45 5 × (-9)=-45 (-5) × (-9)=45

Деление целых чисел

В арифметике целых чисел, если мы a делим на n, мы можем получить q и r. Отношения между этими четырьмя целыми числами можно показать как

В этом равенстве a называется делимое; q — частное; n — делитель и r — остаток. Обратите внимание, что это — не операция, поскольку результат деления a на n — это два целых числа, q и r. Мы будем называть это уравнением деления.

Пример 2.2

Предположим, что a = 255, а n = 11. Мы можем найти q = 23 и r = 2, используя алгоритм деления, из элементарной арифметики

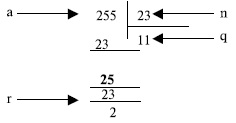
Рис. 2.3.  Пример 2.2, нахождение частного и остатка

Два ограничения

Когда мы используем вышеупомянутое уравнение деления в криптографии, мы налагаем два ограничения. Первое требование: чтобы делитель был положительным целым числом (n > 0). Второе требование: чтобы остаток был неотрицательным целым числом (r > 0). показывает эти требования с двумя указанными ограничениями.

Рис. 2.4.  Алгоритм деления целых чисел

Пример 2.3

Предположим, мы используем компьютер или калькулятор, а r и q отрицательны, при отрицательном a. Как можно сделать, чтобы выполнялось ограничение, что число r должно быть положительным? Решение простое: мы уменьшаем значение q на 1 и добавляем значение n к r, чтобы r стало положительным.

–255 = (–23 × 11) + (–2) ↔ –255 = (–24 × 11) + 9

Мы уменьшили (–23), получили (–24) и добавили 11 к (–2), чтобы получить + 9. Полученное равенство эквивалентно исходному.

Теория делимости

Теперь кратко обсудим теорию делимости — тема, с которой мы часто сталкиваемся в криптографии. Если a не равно нулю, а r = 0, в равенстве деления мы имеем

a = q × n

Мы тогда говорим, что a делится на n (или n — делитель a). Мы можем также сказать, что a делится без остатка на n. Когда мы не интересуемся значением q, мы можем записать вышеупомянутые отношения как a|n. Если остаток не является нулевым, то n не делится, и мы можем записать отношения как a†n.

Пример 2.4

a. Целое число 4 делит целое число 32, потому что . Это можно отобразить как 4|32. Число 8 не делит число 42, потому что . В этом уравнении число 2 — остаток. Это можно отобразить как 8†42.

Пример 2.5

а. Отображение делимости 13|78, 7|98, –6|24, 4|44, и 11 | (–33).

б. Отображение неделимости 13†27, 7†50, – 6†23, 4†41, и 11†(–32).