§ 7. Когерентность и монохроматичность электромагнитного поля
Понятие “когерентность” широко используется в различных областях физики. В § 5 было рассмотрено квантовое описание поля и введено понятие “когерентное состояние”. В классической оптике для характеристики источников излучения по их способности к созданию интерференционной картины также вводится понятие когерентности. Например, если свет от одного источника соответствующим образом разделить на два пучка, а затем наложить их друг на друга, то возникает интерференция – интенсивность от точки к точке будет достигать максимальных и минимальных значений, причем максимальная интенсивность пучков будет превосходить интенсивность одного пучка в предельном случае в четыре раза, а минимальная – стремится к нулю. О таких случаях говорят как о полной или частичной когерентности.
В строго монохроматическом поле амплитуда колебаний в любой точке постоянна, а фаза линейно меняется со временем. Если интерферируют два таких поля, то возникает максимально возможная разница между максимальными и минимальными значениями интенсивности. Волновое поле, создаваемое реальным источником, никогда не бывает монохроматическим. Самая узкая спектральная линия обладает конечной шириной. Амплитуда и фаза волны такого поля испытывают флуктуации (амплитудную и фазовую модуляции), которые могут быть совершенно нерегулярными.
Возмущение,
создаваемое таким источником,
представляется в виде суперпозиции
строго монохроматических волн –
волнового “пакета”. Амплитуда “пакета”
остается более или менее постоянной
лишь в течение времени, малого по
сравнению с длительностью цуга, то есть
при
,
где
- эффективная ширина спектра. В этом
интервале излучение источника подобно
монохроматической волне с некоторой
средней частотой. Таким образом,
длительность цуга может быть характеристикой
когерентности источника в указанном
выше смысле, а время
характеризует время когерентности. Два
таких пучка дадут интерференцию, если
их цуги перекрываются.
Теперь
рассмотрим возмущения в двух точках
пространства поля, созданного некоторым
протяженным квазимонохроматическим
источником. Пусть расстояние от источника
до каждой из этих точек значительно
больше длины волны излучения. Если
разница этих расстояний
для любой исходной точки на поверхности
источника мала по сравнению с длиной
волны, то следует ожидать, что флуктуации
амплитуд и фаз в точках наблюдения будут
одинаковы (при этом расстояние между
точками наблюдения может значительно
превышать длину волны). Более того, между
двумя точками наблюдения может
существовать некоторая корреляция и в
том случае, когда разница между
расстояниями
.
Иными словами, корреляция всегда
существует, когда разница между
расстояниями от любой точки на источнике
до точек наблюдения меньше длины цуга
волнового “пакета”. Следовательно,
вокруг любой точки поля существует
некоторая окрестность когерентности,
а длина
характеризует длину когерентности.
Математическую степень когерентности полей (для одной компоненты поля) можно описать с помощью корреляционных функций
(7.1)
где операторы полей представлены выражениями (5.24) и (5.25) , а усреднение проводится по состоянию электромагнитного поля.
Рассмотрим когерентные состояния поля, определенные, например, формулами (5.30 - 5.33). В этом случае корреляционная функция (7.1) принимает вид
,
(7.2)
то есть в классическом пределе это произведение амплитуд электромагнитного поля, которое обычно описывает интерференционные явления. Для одной моды плоских бегущих волн получим
.
(7.3)
Для
совпадающих координат
и времени
корреляционные функции характеризуют
интенсивность поля в определенный
момент в определенной точке. Легко
видеть, что для рассматриваемых
когерентных состояний поля имеется
следующее соотношение
,
(7.4)
где
индексы 1 и 2 означают совокупности
координат и времени
и
соответственно. Подчеркнем, что последнее
выражение означает необходимое условие
полной когерентности поля в классическом
смысле. Действительно, для определения
интенсивности двух световых полей имеем
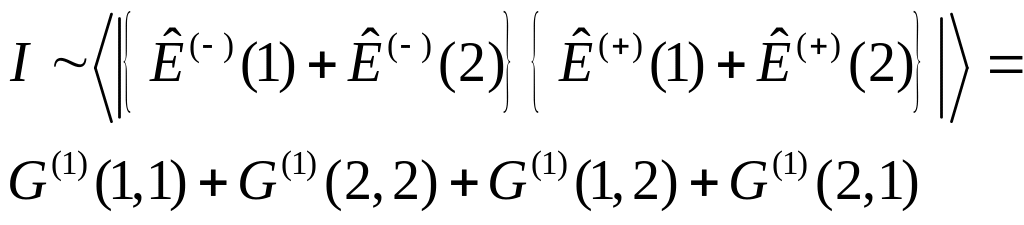(7.5)
Из формулы (7.1) следует, что
,
поэтому (7.5) можно переписать
,
(7.6)
Откуда видно, что максимальная контрастность интерференционной картины достигается при выполнении условия (7.4). Таким образом, когерентное состояние электромагнитного поля является полностью когерентным в рассмотренном выше смысле.
Если ввести нормированную корреляционную функцию
(7.7)
то условие полной когерентности (7.4) принимает вид
(7.8)
Если корреляционную функцию (7.1) можно представить как произведение (7.2),то такое свойство называют факторизацией. Иногда его удобно использовать в качестве определения оптической когерентности первого порядка. Как было показано, корреляционная функция первого порядка описывает интерференционные явления типа опыта Юнга (интерференция излучения при прохождении двух щелей, явления в интерферометре Майкельсона и др.).
В общем случае степень когерентности можно описать корреляционными функциями N-го порядка
(7.9)
где усреднение проводится по состоянию поля, которое описывается некой матрицей плотности
.
(7.10)
Например, корреляционные функции второго порядка описывают интерференционные явления при регистрации излучении двумя независимыми детекторами, например, в радиоинтерферометре Хенбери, Брауна и Твисса [6].