
- •Глава I. Классическое и квантовое описание оптического поля.
- •§ 1. Постулаты квантовой механики и квантовой оптики.
- •§ 2. Классический гармонический осциллятор
- •§3. Квантовый гармонический осциллятор в стационарном состоянии
- •§ 4. Квантовый гармонический осциллятор в когерентном состоянии
- •5. Квантование электромагнитного поля в вакууме
- •§ 6. Уравнения максвелла для поля в среде
- •§ 7. Когерентность и монохроматичность электромагнитного поля
- •Глава II. Рапространение электромагнитной волны в нелинейной среде.
- •§ 8. Общие представления о нелинейном отклике среды
- •§ 9. Нелинейная геометрическая оптика
- •§ 10. Нелинейное параболическое уравнение
- •§ 11. Устойчивость плоской волны в нелинейной среде
- •§ 12. Солитоны
- •§ 13. Самофокусировка и самоканализация
- •Глава III. Нелинейные восприимчивости
- •§14. Нелинейная связь между поляризацией и электрическим полем
- •§15. Классификация нелинейно-оптических эффектов
- •§16. Модель ангармонического осциллятора
- •§17. Общая теория нелинейных восприимчивостей для произвольной квантовомеханической системы
- •Глава IV. Нелинейные волновые взаимодействия
- •§18. Генерация оптических гармоник
- •§19. Пространственный синхронизм
- •§20. Резонансная генерация третьей гармоники
- •§21. Методы создания фазового согласования
- •22. Параметрические взаимодействия
- •§23. Вынужденное рассеяние мандельштама-бриллюэна (врмб)
- •Глава V. Фотоионизация лазерным излучением
- •§ 24. Трехступеньчатая фотоионизация в сильном лазерном поле
- •§ 25. Кинетические уравнения при фотоионизации оптически тонкого слоя.
- •§ 26. Метод матрицы плотности для фотоионизации.
- •§ 27. Макроскопический дипольный момент
- •§ 28. Однофотонные, ступеньчатые и двухфотонные процессы
- •§ 29.Уравнение для матрицы плотности в энергетическом
- •§ 30. Модель двухуровневой системы для фотоионизации
- •§ 31. Модель трехуровневой системы для фотоионизации
- •Постулаты класической механики
- •Постулаты нерелятивисткой квантовой механики
- •3.Уравнениие движения
- •4.Правило нахождения Гамильтониана
- •5.Постулат тождественности
§ 4. Квантовый гармонический осциллятор в когерентном состоянии
Определим
когерентное
состояние
как собственный вектор оператора
уничтожения
,
обладающего собственной функцией
![]() и собственным значением
в соответствии с их стандартным
определением в квантовой теории:
и собственным значением
в соответствии с их стандартным
определением в квантовой теории:
![]() (4.1)
(4.1)
где есть комплексное число. Когерентное состояние разложим в ряд типа (3.10) по полной ортонормированной системе собственных векторов оператора чисел заполнения (3.30):
![]() (4.2)
(4.2)
Чтобы
найти коэффициенты разложения, т.е.
проекции
![]() ,
умножим скалярно (4.1) на бра-вектор
и,
воспользовавшись правилами (3.29), получим
цепочку равенств:
,
умножим скалярно (4.1) на бра-вектор
и,
воспользовавшись правилами (3.29), получим
цепочку равенств:
![]() (4.3)
(4.3)
Произведем нормировку когерентного состояния на единицу, т.е. будем полагать, что скалярное произведение
![]() (4.4)
(4.4)
Подставим в (4.4) разложение(4.2). Учитывая ортонормированность собственных векторов , т.е.
![]() (4.5)
(4.5)
получим, что
![]() (4.6)
(4.6)
Теперь подставим в (4.6) вместо последнее равенство из (4.3). В результате получим
![]() (4.7)
(4.7)
откуда следует, что
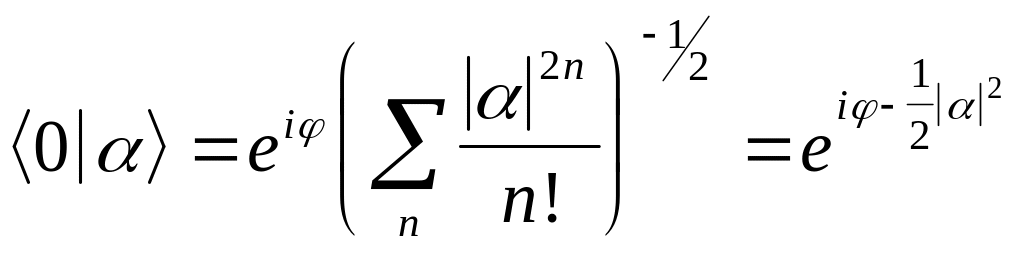 (4.8)
(4.8)
где
![]() есть произвольное число. Иными словами,
из условия нормировки (4.4) можно получить
проекцию
есть произвольное число. Иными словами,
из условия нормировки (4.4) можно получить
проекцию
![]() с точностью до произвольной фазы. Полагая
с точностью до произвольной фазы. Полагая
![]() ,
окончательно получим выражение (4.2) для
когерентного состояния одномерного
(одномодового) гармонического осциллятора
в виде
,
окончательно получим выражение (4.2) для
когерентного состояния одномерного
(одномодового) гармонического осциллятора
в виде
![]() (4.9)
(4.9)
Отсюда
видно, что когерентное состояние при
![]() является в то же время основным состоянием,
при котором
,
т.е. оно является единственным основным
состоянием осциллятора. Из (4.3) и (4.8)
однозначно следует также, что вероятность
обнаружить осциллятор в n-ом
энергетическом состоянии
является в то же время основным состоянием,
при котором
,
т.е. оно является единственным основным
состоянием осциллятора. Из (4.3) и (4.8)
однозначно следует также, что вероятность
обнаружить осциллятор в n-ом
энергетическом состоянии
![]() (4.10)
(4.10)
откуда
видно, что вероятность заполнения
состояния
есть распределение
Пуассона
со средним значением
![]() .
.
Любое когерентное состояние можно получить из основного состояния, заменив собственный вектор оператора чисел заполнения в соответствии с формулой (3.31). После замены получаем выражение
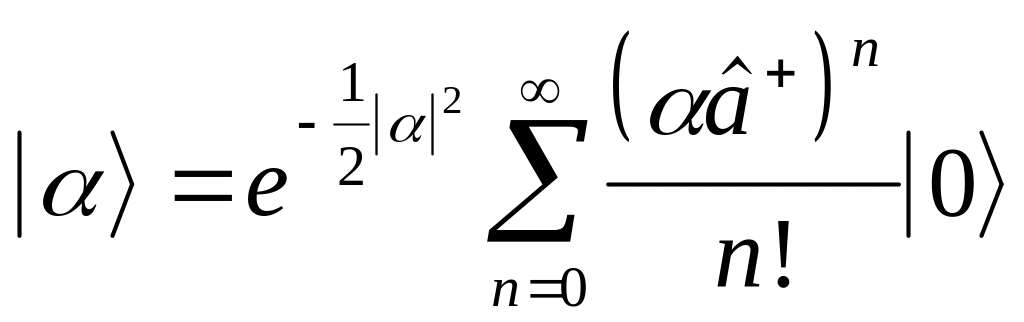 (4.11)
(4.11)
которое в общем виде означает, что
![]() (4.12)
(4.12)
где
![]() есть некоторый оператор
сдвига,
частный вид которого определяется
сравнением (4.12) с (4.11) Таким образом,
когерентные состояния представляют
собой в точности основное состояние
осциллятора, на которое подействовали
оператором сдвига
.
есть некоторый оператор
сдвига,
частный вид которого определяется
сравнением (4.12) с (4.11) Таким образом,
когерентные состояния представляют
собой в точности основное состояние
осциллятора, на которое подействовали
оператором сдвига
.
Из
условия нормировки (4.4) следует, что
оператор
есть унитарный оператор, т. е. он
удовлетворяет условию:
![]() Далее, если учесть, что из очевидного
условия
Далее, если учесть, что из очевидного
условия
![]() следует также условие
следует также условие
![]() ,
которое эквивалентно действию единичного
оператора, то унитарный оператор
можно представить в виде
,
которое эквивалентно действию единичного
оператора, то унитарный оператор
можно представить в виде
![]() (4.13)
(4.13)
Воспользовавшись известной формулой
![]() (4.14)
(4.14)
которая
справедлива для коммутатора
![]() ,
коммутирующего в свою очередь с любым
из
,
коммутирующего в свою очередь с любым
из
![]() и
и
![]() ,
получим вид оператора сдвига в компактном
форме:
,
получим вид оператора сдвига в компактном
форме:
![]() (4.15)
(4.15)
Этот оператор сдвига обладает следующими свойствами:
![]()
![]() (4.16)
(4.16)
![]()
Теперь
обратим внимание на тот важный факт,
что набор когерентных состояний
удовлетворяет условию полноты, нормировки,
но не удовлетворяет условию ортогональности.
Последнее свойство легко доказать путем
прямого вычисления скалярного произведения
![]() на основе формул (4.5) и (4.9). В результате
получим следующее выражение
на основе формул (4.5) и (4.9). В результате
получим следующее выражение
![]() (4.17)
(4.17)
откуда
находим, что абсолютное значение
скалярного произведения сводится к
простой экспоненциальной зависимости:
![]() .
Следовательно, когерентные состояния
строго не ортогональны, хотя они почти
ортогональны при значениях
.
Следовательно, когерентные состояния
строго не ортогональны, хотя они почти
ортогональны при значениях
![]() много больше единицы. Для значений
,
близких к
много больше единицы. Для значений
,
близких к
![]() ,
происходит сильное перекрытие волновых
функций, аналогичных по форме. Заметим,
однако, что ортогональность набора
базисных состояний не является необходимым
свойством для разложения по ним
произвольных состояний. Более важным
и необходимым в этом случае является
свойство полноты. Это положение, в
некотором смысле, эквивалентно разложению
обычных векторов на проекции по осям в
прямоугольных и косоугольных системах
координат.
,
происходит сильное перекрытие волновых
функций, аналогичных по форме. Заметим,
однако, что ортогональность набора
базисных состояний не является необходимым
свойством для разложения по ним
произвольных состояний. Более важным
и необходимым в этом случае является
свойство полноты. Это положение, в
некотором смысле, эквивалентно разложению
обычных векторов на проекции по осям в
прямоугольных и косоугольных системах
координат.
Набор когерентных состояний является полным, т.е. удовлетворяет соотношению
![]() (4.18)
(4.18)
где
интегрирование осуществляется по всей
-плоскости,
а дифференциальный элемент площади
![]() ,
и он есть действительная величина. Для
доказательства воспользуемся кет-вектором
(4.9)
и соответствующим ему бра-вектором
,
и он есть действительная величина. Для
доказательства воспользуемся кет-вектором
(4.9)
и соответствующим ему бра-вектором
![]() :
:
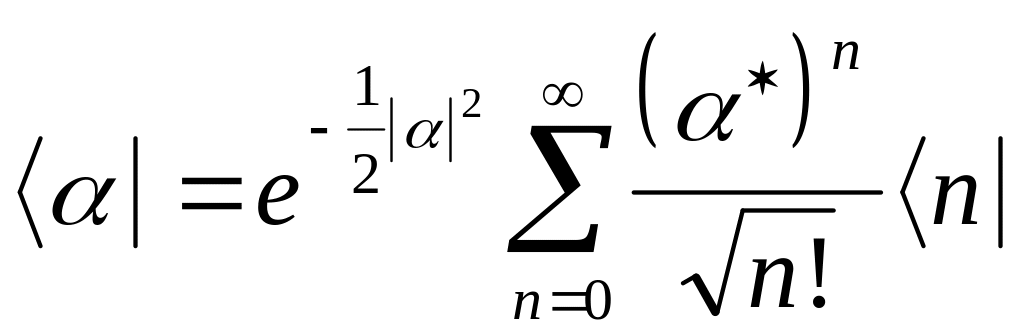 (4.19)
(4.19)
Представим
комплексную
![]() .
Тогда в полярных координатах дифференциал
.
Тогда в полярных координатах дифференциал
![]() ,
а двойной интеграл в (4.18) с учётом (4.19)
преобразуется к произведению однократных
определенных интегралов по
,
а двойной интеграл в (4.18) с учётом (4.19)
преобразуется к произведению однократных
определенных интегралов по
![]() и
:
и
:
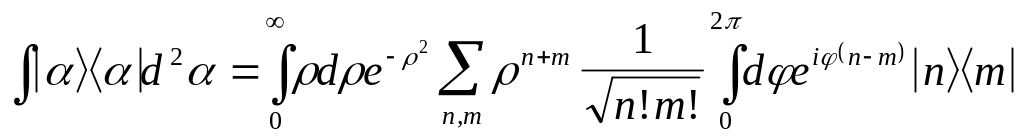 =
=
![]() =
=![]() (4.20)
(4.20)
где
![]() есть гамма-функция:
есть гамма-функция:
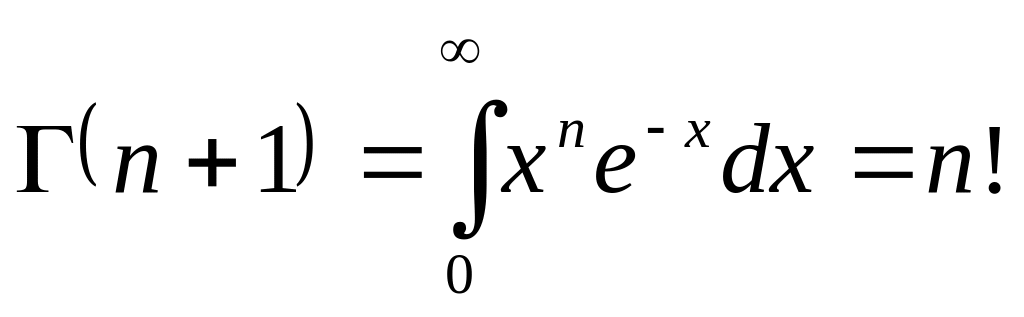 .
Интегрирование по азимутальному углу
дает в результате величину
.
Интегрирование по азимутальному углу
дает в результате величину
![]() .
Поскольку хорошо известно, что состояния
образуют полный ортонормированный
базис, то мы имеем
.
Поскольку хорошо известно, что состояния
образуют полный ортонормированный
базис, то мы имеем
![]() ,
и, следовательно, с учётом (4.20), справедливо
условие полноты и для когерентных
состояний (4.18).
,
и, следовательно, с учётом (4.20), справедливо
условие полноты и для когерентных
состояний (4.18).
С помощью вышеприведенных в этом параграфе определений и свойств когерентных состояний одномодового осциллятора рассмотрим различные средние значения механических величин. Прежде всего, обратим внимание, что от упорядоченного произведения операторов рождения и уничтожения и легко рассчитывать средние значения когерентных состояний [6]. Например, из выражений (3.20) и определения (4.1) следует:
![]()
(4.21)
![]()
Далее из (3.24) и определения (4.1) получаем
![]() (4.22)
(4.22)
Из последних формул (4.21) и (4.22) видно, что в когерентном состоянии
![]()
(4.23)
![]()
Как и следовало ожидать, в общем случае когерентные состояния не являются стационарными: вероятность обнаружить осциллятор в конкретном энергетическом состоянии с определенной энергией дается распределением Пуассона (4.10). Среднеквадратичное отклонение для n, вычисленное с помощью пуассоновского распределения, приводит, как известно к результату (см. напр. [1]):
![]() (4.24)
(4.24)
При
малых
![]() и для больших
и для больших
![]() распределение Пуассона переходит в
распределение Гаусса. В этом случае
необходимо воспользоваться асимптотической
формулой Стирлинга для факториала
большого числа:
распределение Пуассона переходит в
распределение Гаусса. В этом случае
необходимо воспользоваться асимптотической
формулой Стирлинга для факториала
большого числа:
![]() .
Используя (4.10) и разложив
.
Используя (4.10) и разложив
![]() в ряд по степеням
в ряд по степеням
![]() ,
получаем гауссово распределение
вероятностей
,
получаем гауссово распределение
вероятностей
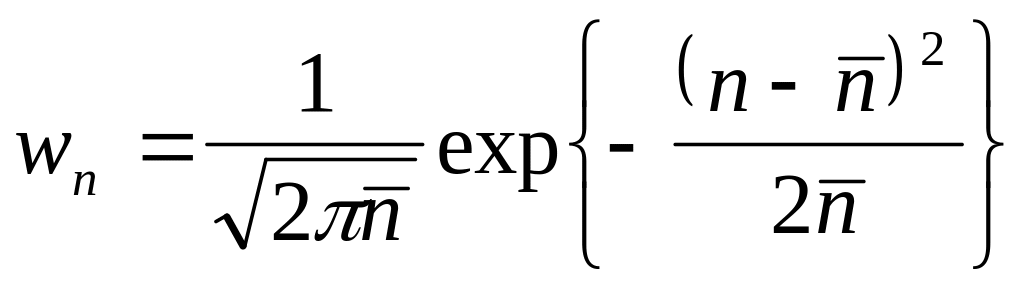 (4.25)
(4.25)
Теперь найдём волновые функции (3.11) и (3.12), или, другими словами, проекции вектора когерентного состояния в координатном и импульсном представлениях. Подставим в исходное выражение (4.1) оператор уничтожения из (3.20), получим
![]() (4.26)
(4.26)
Умножим
в этом выражении скалярно обе части
равенства на сопряженные состояния
![]() и
и
![]() ,
а затем воспользуемся определениями
дифференциальных операторов координаты
и импульса согласно постулатам квантовой
механики ( см. Прил. 1). Они имеют вид:
,
а затем воспользуемся определениями
дифференциальных операторов координаты
и импульса согласно постулатам квантовой
механики ( см. Прил. 1). Они имеют вид:
а) в q-представлении
![]()
(4.27)
![]()
б) в p-представлении
![]()
(4.28)
![]()
В результате из (4.26) с учетом (4.27) и (4.28) получаем дифференциальные уравнения для волновых функций (3.11) и (3.12) в виде
а) в q-представлении
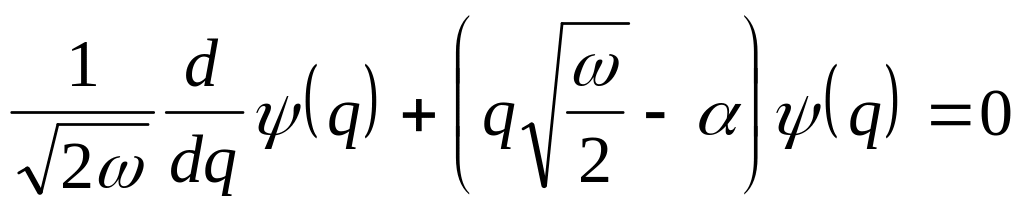 (4.29)
(4.29)
б) в p-представлении
![]() (4.30)
(4.30)
Эти
линейные уравнения (4.29) и (4.30) можно
проинтегрировать и получить решения
для волновых функций
![]() и
и
![]() ,
которые в нормированном виде представлены
следующими выражениями[6]:
,
которые в нормированном виде представлены
следующими выражениями[6]:
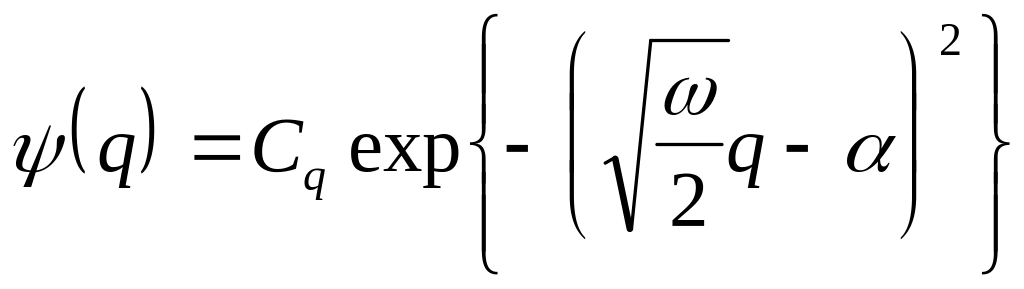 (4.31)
(4.31)
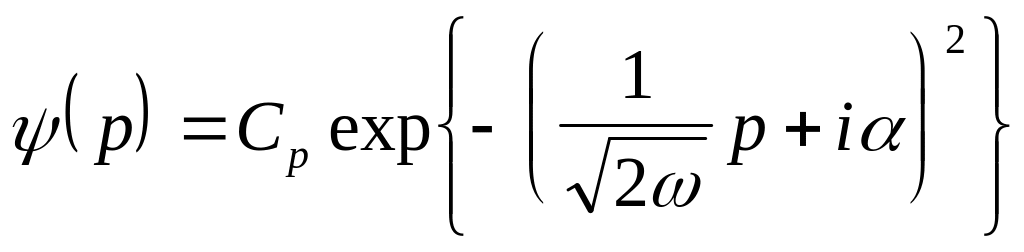 (4.32)
(4.32)
где
нормировочные константы
 и
и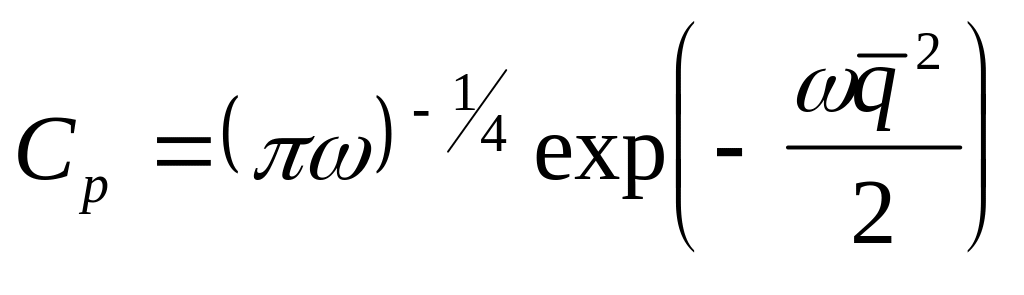 .
.
Обе
волновые функции при
совпадают с явным видом проекций вектора
основного состояния в координатном и
импульсном представлениях (3.35). При
любых
![]() они представляют собой волновые функции
основного состояния осциллятора, на
которые подействовал оператор сдвига
(4.13).
они представляют собой волновые функции
основного состояния осциллятора, на
которые подействовал оператор сдвига
(4.13).
До
сих пор в этом параграфе говорилось о
гейзенберговском представлении, в
котором вектор состояния квантовой
системы не зависит от времени, а вся
зависимость от времени содержится в
операторах. Перейдем к рассмотрению
шредингеровского представления, где
временная зависимость содержится в
векторах состояний. Соотношение (3.3)
связывает векторы состояний в обоих
представлениях. В качестве гамильтониана
осциллятора возьмем выражение (3.24),
опустив второе слагаемое
![]() ,
так как оно дает одинаковый для всех
состояний фазовый множитель, которым
можно пренебречь. Подставляя (3.24) в (3.3)
и учитывая (4.9), получаем следующую
цепочку равенств вектора когерентного
состояния в шредингеровском представлении:
,
так как оно дает одинаковый для всех
состояний фазовый множитель, которым
можно пренебречь. Подставляя (3.24) в (3.3)
и учитывая (4.9), получаем следующую
цепочку равенств вектора когерентного
состояния в шредингеровском представлении:
![]() (4.33)
(4.33)
Итак,
соответствующее шредингеровское
состояние принимает такой же вид, как
и гейзенберговское выражение (4.9), если
заменить
на
![]() .
Заменяя в формулах (4.21), (4.31) и (4.32)
символом
получаем, что средние значения
.
Заменяя в формулах (4.21), (4.31) и (4.32)
символом
получаем, что средние значения
![]() и
и
![]() квантового осциллятора в когерентном
состоянии совершают те же гармонические
колебания, что и классический осциллятор
(2.9), причём амплитуды колебаний
и
равны
квантового осциллятора в когерентном
состоянии совершают те же гармонические
колебания, что и классический осциллятор
(2.9), причём амплитуды колебаний
и
равны
![]() и
и
![]() соответственно. Иначе говоря, для средних
и
справедливы уравнения движения
классического гармонического осциллятора
(2.6) и их решения (2.7), в которых амплитуда
А заменяется на
.
Отсюда также следует, что выражения
(4.31) и (4.32) остаются справедливыми и в
шредингеровском представлении, если
дополнительно ввести множитель
соответственно. Иначе говоря, для средних
и
справедливы уравнения движения
классического гармонического осциллятора
(2.6) и их решения (2.7), в которых амплитуда
А заменяется на
.
Отсюда также следует, что выражения
(4.31) и (4.32) остаются справедливыми и в
шредингеровском представлении, если
дополнительно ввести множитель
![]() при величине
.
Гауссова плотность вероятности для
произвольного когерентного состояния,
которая по форме совпадает с аналогичной
формой для основного состояния, также
обладает колебательным характером
движения. Рассмотрим это детальнее.
при величине
.
Гауссова плотность вероятности для
произвольного когерентного состояния,
которая по форме совпадает с аналогичной
формой для основного состояния, также
обладает колебательным характером
движения. Рассмотрим это детальнее.
Подставим в виде (4.23) в (4.31) и (4.32). В результате простых алгебраических преобразований получим и в виде волновых пакетов:
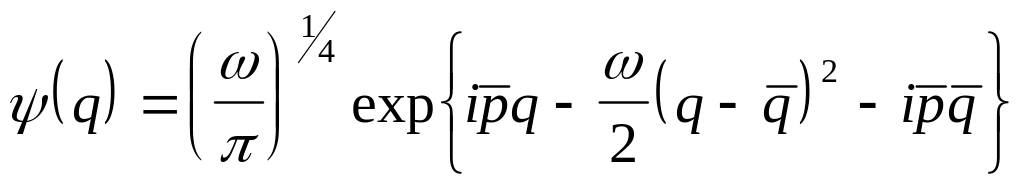
(4.34)
![]()
Поскольку
зависимость от времени средних
и
полностью определена, то из формул
(4.34) также можно увидеть, что когерентное
состояние одномерного осциллятора
представляет собой волновой пакет,
который не расплывается с течением
времени. Центр пакета в фазовой плоскости
![]() и
находится в точке с "координатами"
и
находится в точке с "координатами"
![]() и
и совершает движение по круговой орбите,
которая полностью совпадает с круговой
траекторией классического гармонического
осциллятора, если вместо А в (2.7) поставить
радиус окружности, равный
и
и совершает движение по круговой орбите,
которая полностью совпадает с круговой
траекторией классического гармонического
осциллятора, если вместо А в (2.7) поставить
радиус окружности, равный
![]() (4.35)
(4.35)
Вероятность
измерения![]() в некоторый момент времени координаты
в интервале
в некоторый момент времени координаты
в интервале
![]() и
импульса
в
интервале
и
импульса
в
интервале
![]() задается функцией распределения
(плотностью вероятности) вида
задается функцией распределения
(плотностью вероятности) вида
![]() (4.36)
(4.36)
Подставляя в (4.36) выражения (4.34), получаем
![]() (4.37)
(4.37)
которое перепишем в форме распределения Гаусса (3.37), а именно
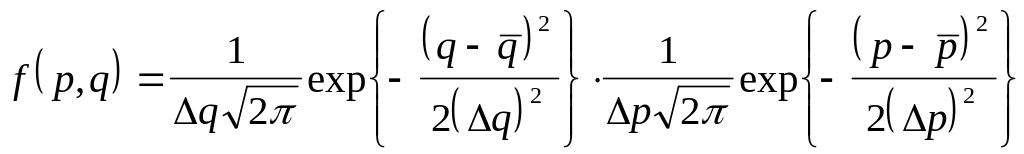
где
![]()
(4.38)
![]()
Произведение
![]() ,
и это означает, что когерентное состояние
представляет собой волновой пакет с
наименьшей неопределенностью, допускаемой
квантовой теорией для значений координаты
и импульса.
,
и это означает, что когерентное состояние
представляет собой волновой пакет с
наименьшей неопределенностью, допускаемой
квантовой теорией для значений координаты
и импульса.
В
виду особой важности последнего вывода
получим соотношение неопределенностей
в когерентном состоянии осциллятора
ещё раз другим способом. При этом дадим
вывод и конечные результаты в физической
системе единиц esu.
В этих единицах вместо (3.20) выражения
операторов
и
![]() должны быть записаны в виде
должны быть записаны в виде
![]()
(4.39)
![]()
из которых получаем, что
![]()
(4.40)
![]()
Вычисление средних в когерентных состояния удобно проводить от упорядоченного произведения операторов рождения и уничтожения. В упорядоченном произведении операторы должны стоять слева от операторов . Усреднение производится по формуле:
![]()
![]()
![]() ,
,
(4.41)
справедливость
которой следует из определения когерентных
состояний (4.1). Любое произведение
расположенных в произвольном порядке
операторов
и
преобразуется в сумму упорядоченных
произведений этих же операторов путем
последовательного применения правила
коммутации операторов рождения и
уничтожения:
![]() .
.
В
качестве примера проведем вычисление
среднеквадратичных отклонений координаты
и импульса осциллятора, находящегося
в когерентном состоянии, следуя общим
формулам (3.32). Воспользуемся выражениями
(4.40) и запишем
![]() и
в виде суммы упорядоченных произведений
операторов
и
:
и
в виде суммы упорядоченных произведений
операторов
и
:
=![]() =
=![]() =
=![]()
(4.42)
=![]() =
=![]() =
=![]()
Вычисление средних значений операторов и по формуле (4.41) дает
![]()
(4.43)
![]()
Средние
значения
и
получены были ранее в виде (4.21). В системе
единиц esu
![]() и
и
![]() равны
последним слагаемым в выражениях (4.43)
соответственно. Подставляя (4.43) и
соответствующие выражения для
и
в (3.32), окончательно получаем
равны
последним слагаемым в выражениях (4.43)
соответственно. Подставляя (4.43) и
соответствующие выражения для
и
в (3.32), окончательно получаем
![]()
![]() (4.44)
(4.44)
![]()
Сопоставление выражений (3.34) и (4.44) показывает, что когерентное состояние одномерного гармонического осциллятора обладает минимально возможным соотношением неопределенностей для координаты и импульса при любых значениях , а следовательно, при любых средних значениях чисел заполнения по сравнению со стационарным состоянием того же осциллятора, который обладает этим свойством только при .
На
рис. 3
в фазовой плоскости
и
изображены кривые
![]() ,
которые представляют собой множество
концентрических окружностей вокруг
центра пакета, т.е. вокруг точки
и
,
которая, в свою очередь, вращается по
кругу радиуса
,
которые представляют собой множество
концентрических окружностей вокруг
центра пакета, т.е. вокруг точки
и
,
которая, в свою очередь, вращается по
кругу радиуса
![]() (4.35) с угловой скоростью
.
Угол поворота радиус-вектора центра
пакета определяет среднее значение
фазы
(4.35) с угловой скоростью
.
Угол поворота радиус-вектора центра
пакета определяет среднее значение
фазы
![]() квантового осциллятора в когерентном
состоянии в полной аналогии со случаем
классического осциллятора (см. рис.1).
квантового осциллятора в когерентном
состоянии в полной аналогии со случаем
классического осциллятора (см. рис.1).
Неопределенность
фазы можно оценить следующим образом.
Проведем из центра круговой фазовой
траектории радиуса
( из начала координат ) два луча, которые
будут касаться окружности с центром в
точке
и
.
Диаметр этой окружности возьмём равным:
![]() ,
т.е. он определяется среднеквадратичными
отклонениями координаты и импульса
квантового осциллятора в когерентном
состоянии. Интервал углов
,
т.е. он определяется среднеквадратичными
отклонениями координаты и импульса
квантового осциллятора в когерентном
состоянии. Интервал углов
![]() ,
ограниченный этими двумя лучами,
оказывается равным
,
ограниченный этими двумя лучами,
оказывается равным
![]() (4.45)
(4.45)
а
произведение неопределенностей
из(4.45) и
![]() из (4.24) дает в результате
из (4.24) дает в результате
![]() (4.46)
(4.46)
которое
справедливо при любых значениях
![]() .
Корректное рассмотрение операторов
фазы
.
Корректное рассмотрение операторов
фазы
![]() и чисел заполнения
и чисел заполнения
![]() ,
а также состояний квантового гармонического
осциллятора с точно определенной фазой
или точно определенной амплитудой можно
найти в монографии [13].
,
а также состояний квантового гармонического
осциллятора с точно определенной фазой
или точно определенной амплитудой можно
найти в монографии [13].
