§3. Квантовый гармонический осциллятор в стационарном состоянии

В квантовой теории состояние системы характеризуется вектором состояния в некотором линейном гильбертовом пространстве [2]. Согласно постулатам квантовой механики (см. приложение 1A) измеримыми на опыте величинами p и q являются собственные значения соответствующих эрмитовых операторов и .

Среднее значение любого оператора определяется формулой

(3.1)

Эволюция квантовой системы может быть описана несколькими эквивалентными способами (представлениями).

В шредингеровском представлении операторы не зависят от времени. Зависимость от времени содержится в векторе состояния и определяется путём решения уравнения Шредингера

(3.2)

или в иной форме - посредством воздействия на начальное состояние унитарного оператора эволюции :

(3.3)

где - гамильтониан квантовой системы.

Если вектор состояния считать независящим от времени, то из формул (3.1) и (3.3) следует, что необходимо ввести зависимость операторов от времени следующим образом:

(3.4)

или, дифференцируя выражение (3.4) по времени, представить в такой форме

(3.5)

Такое представление называют гейзенберговским. Оно в некотором смысле соответствует классическому описанию (сравни с уравнением (2.2)), где скобки Пуассона заменяются коммутатором: . Очевидно, что оба представления -шредингеровское и гейзенберговское-приводят к одинаковым средним значениям:

(3.6)

Любой вектор состояния в линейном гильбертовом пространстве может быть задан на некотором базисе. Если в качестве базиса выбрать собственные векторы оператора координаты

(3.7)

которые удовлетворяют необходимым свойствам полноты

(3.8)

и ортонормированности

(3.9)

то вектор состояния можно записать в виде разложения

(3.10)

где скалярное произведение как функция координат

(3.11)

есть проекция вектора на ось с направлением в координатном представлении.

Аналогично можно выбрать в качестве базиса собственные векторы оператора импульса. Проекции вектора состояния в импульсном представлении имеют формально такой же вид

(3.12)

Оба представления связаны между собой посредством соотношения

(3.13)

Рассмотрим состояние квантового гармонического осциллятора, которое является собственным вектором гамильтониана

(3.14)

Из (3.5) видно, что для замкнутой системы оператор не зависит от времени. Положим

(3.15)

где - собственный вектор гамильтониана (оператора энергии), т.е.

(3.16)

с собственными значениями (спектр энергий гармонического осциллятора)

(3.17)

Здесь и далее используется атомная система единиц: . Переход в гауссову систему единиц (esu) или международную (SI) будет оговариваться особо в каждом конкретном случае..

Эти состояния называют стационарными, или энергетическими. Волновые функции и гармонического осциллятора в стационарных состояниях, или, другими словами, проекции вектора имеют следующий вид (соответственно в q- и p-представлениях) [18]:

=

(3.18)

=

где функции есть полиномы Эрмита n-ой степени от переменной , определяемые производящей формулой

= (3.19)

Вместо операторов координаты и импульса удобно ввести ( в гейзенберговском представлении ) операторы рождения и уничтожения и следующего вида:

(3.20)

Операторы и связаны с операторами и линейными преобразованиями (3.20), которые полностью совпадают с соответствующими преобразованиями между каноническими переменными и и динамическими переменными и (2.9) при описании классического гармонического осциллятора в § 1.2. Исходя из последних формул (3.20), выразим в явном виде и через и , возведём в квадратную степень и подставим в гамильтониан (3.14). После приведения подобных членов, получим гамильтониан осциллятора, зависящий от операторов рождения и уничтожения, в виде

(3.21)

который полностью совпадает с видом (2.10) функции Гамильтона осциллятора в канонических переменных и . Используя коммутатор для координаты и импульса

(3.22)

а также выражения (3.20) легко получить коммутатор для операторов рождения и уничтожения:

(3.23)

Гамильтониан (3.21) с учётом коммутатора (3.23) преобразуется к виду

(3.24)

Существенное отличие от классического осциллятора заключается в наличии слагаемого 1/2 в гамильтониане квантового гармонического осциллятора.

Далее, используя уравнение движения для операторов в гейзенберговском представлении (3.5) и коммутатор (3.23), получим уравнения движения операторов рождения и уничтожения в виде

(3.25)

Общие решения уравнений (3.25) имеют вид экспоненциальных функций:

(3.26)

Полученные выражения (3.25) и (3.26) совпадают по форме с соответствующими уравнениями и их решениями в классическом случае (2.13) и(2.14). В шредингеровском представлении необходимо пользоваться операторами, и , независящими от времени. Всюду далее мы будем пользоваться гейзенберговским представлением, оговаривая случаи, когда будем переходить к шредингеровскому. При этом будем опускать скобки с временными аргументами (t) и (0).

Матричные элементы оператора координаты и импульса определенные на базисе собственных векторов оператора энергии, имеют следующие значения, отличные от нуля[18]:

(3.27)

а для операторов рождения и уничтожения из формул (3.20) и (3.27) получим

(3.28)

Из последних выражений для матричных элементов следует, что действие операторов и на стоящие справа от них собственные вектора энергии (кет-вектор - по дираковской терминологии) и на стоящие слева от них собственные вектора (бра-вектор ),определяется правилами:

(3.29)

Видно, что действие операторов рождения и уничтожения и на кет-вектор приводит соответственно к увеличению и уменьшению энергетического состояния на квант . Оператор

(3.30)

называется оператором чисел заполнения. Из правил (3.29) видно, что собственный вектор оператора энергии является в тоже время и собственным вектором оператора чисел заполнения , поскольку . Собственное значение оператора есть квантовое число n, т.е. натуральный ряд чисел n=0, 1, 2, …

В матричной форме кет- вектор представляет собой бесконечную матрицу, состоящую из одного столбца с нулевыми элементами, кроме n+1 -ой строки, где стоит единица; бра-вектор представляет собой бесконечную матрицу, состоящую из одной строки с нулевыми элементами, кроме n+1 -ого столбца, где стоит единица. Ортонормированность и полнота этих n-квантовых состояний легко проверяется путем перемножения соответствующих матриц по правилу "строка на столбец":

(3.31)

Например, скалярное произведение , т.е. символу Кронекера. Далее, произведение , называемое внешним произведением, или проекционным оператором, сводится к бесконечной матрице с нулевыми элементами, кроме одного диагонального, равного единице и стоящего в n-ой строке (столбце). Очевидно, что сумма по всем n слагаемым даст единичную матрицу, т.е. удовлетворяет условию полноты.

Низшее, основное состояние гармонического осциллятора характеризуется нулевым квантовым числом (n = 0) и вектором состояния .

Согласно первой формуле в (3.29) последовательное действие оператора рождения на вектор основного состояния n-раз приводит к образованию возбужденного состояния , которое можно представить в компактной форме:

(3.32)

Как известно, средние значения координаты и импульса в любом стационарном состоянии равны нулю. Это непосредственно следует формул (3.20) и (3.29). Поэтому состояния не могут, в принципе, соответствовать решениям для движения классического осциллятора по определенной траектории. На рис.2 приведен пример распределения плотности вероятности для координат линейного гармонического осциллятора. Это распределение демонстрирует резко осциллирующую зависимость в пространстве, мало похожую на соответствующие плотности для классического случая. Из выражений (3.18) хорошо видно, что аналогичное распределение плотности вероятности имеет место для импульсов .

В заключении этого параграфа дадим вывод соотношения неопределенности для координаты и импульса в случае линейного гармонического осциллятора. Введем величины и , характеризующие корни из среднеквадратичных отклонений импульса p и координаты q от своих средних значений и в виде:

(3.33)

Положим , и вычислим средние от квадратов операторов и по формуле умножения матриц (3.31). Учитывая, что ненулевыми матричными элементами операторов и в энергетическом базисе являются лишь недиагональные, приведенные в (3.27), получим из (3.33) для среднеквадратичных отклонений и соотношения неопределенностей хорошо известные выражения:

(3.34)

Здесь в (3.34) окончательные формулы представлены в системе (esu).

Отсюда видно, что наименьшее значение соотношение неопределенностей имеет при n=0, т.е. в основном состоянии.

Для дальнейшего изложения приведём явный вид проекций вектора основного состояния в координатном и импульсном представлениях, и другим путем получим соотношение неопределенностей в низшем по энергии состоянии осциллятора. Если в (3.18) положить n=0, то нетрудно убедиться, что в обоих представлениях эти проекции описываются функциями распределения Гаусса:

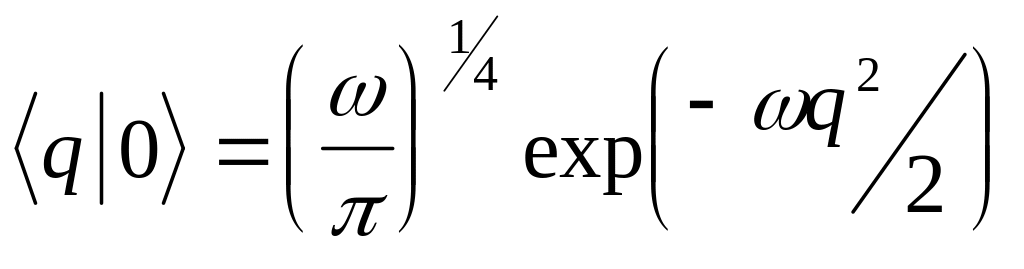
(3.35)

Отсюда видно, что соответствующие плотности вероятностей для координат и импульсов имеют следующее гауссово распределение

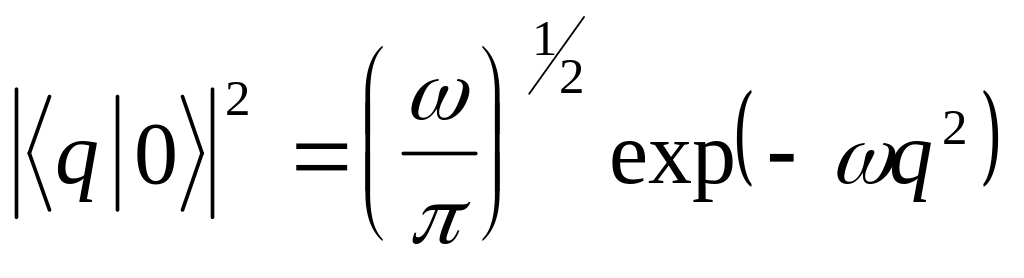
(3.36)

Сравнивая эти выражения (3.36) с канонической формой распределения Гаусса

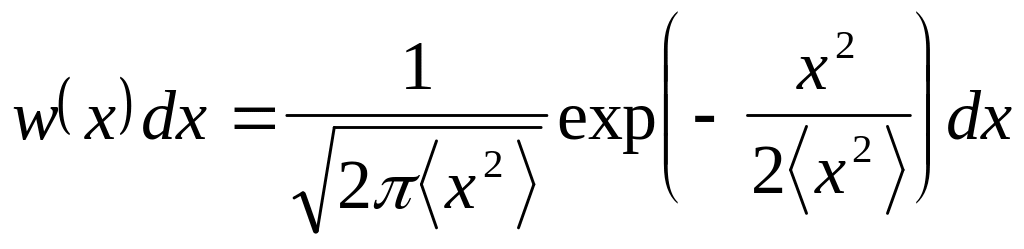(3.37)

найдём, что , а . Следовательно, для основного состояния произведение , т.е. имеет минимально возможное значение как и должно быть при согласно (3.34). Подчеркнем ещё раз, что, таким образом, волновые функции основного состояния линейного гармонического осциллятора (3.35) обладают минимальным соотношением неопределенностей, по сравнению с возбужденными и особенно с высоковозбужденными состояниями.

Возникает естественный вопрос, существуют ли такие состояния осциллятора, кроме основного, которые бы также минимизировали соотношение неопределенностей. В следующем параграфе мы подробно опишем когерентное состояние осциллятора, которое обладает именно каким свойством.