§ 31. Модель трехуровневой системы для фотоионизации

Аналогичная процедура применима для рассмотрения трехуровневой схемы фотоионизации. Очевидным образом обобщается система уравнений для матрицы плотности (30.1). Схема уровней для рассматриваемой модели показана на Рис. 3. Аналогичным образом, как в случае двухуровневой схемы можно ввести релаксацию. Математически удобно сформулировать всю процедуру трехуровневой схемы фотоионизации исходя из наглядного примера когерентного взаимодействия света с веществом, т.е. практически это означает, что импульсы достаточно короткие по сравнению с характерными временами релаксации T и ₀₁, ₁₂ и т.п. Затем сделать обобщение на длинные оптические импульсы.

Рис. 3. Трехуровневая схема фотоионизации.

Итак, рассмотрим изолированный атом в трех лазерных полях с частотами 1, 2 и 3 ( рад/с = 2 Гц) и амплитудами электри­ческого поля E1, E2 и E3. Оптические расстрой­ки определяются так же, как и в предыдущем случае (см. § 30) . Мы будем использовать в этом параграфе те же определения и те же обозначения для амплитуд полей, их частот и атомных переходов, что и § 30: 10 = 1 – 10, 21 = 2 – 21 (см. Рис. 3). Последний шаг ионизации, т.е. возбуждение атома с уровня 2 в непрерывный спектр,

будет описывать эффективность фотоионизации

_i = _i I_i T_i (31.1)

где индекс i  указывает на то, что все входящие сюда величины относятся к последней стадии ионизации (I_i  – лазерная интенсивность, связанная с амплитудой поля I_i =  ,  T_i – длительность лазерного импульса). Сечение трехступенчатой ионизации, которая в ряде простейших случаев определяется формулой _i = ₂(t)_2i , где ₂(t) есть населенность уровня энергии ₂ в некоторый фиксированный момент времени, а _2i есть поперечное сечение ионизации атома, когда он находится в возбужденном состоянии . Вероятность обнаружить атом в состоянии определяется эффективностью возбуждения атома полями E₁ (для перехода из основного состояния с энергией ₀ в промежуточное с энергией ₁) и E₂ (для перехода из состояния в возбужденное состояние с энергией ₂). В случае когерентного взаимодействия ₂(t)=  , где а₂ есть амплитуда вероятности обнаружить квантовую систему в состоянии . Влияние непрерывного спектра и автоионизационных состояний должно учитываться при расчете сечения ₂. Мы подчеркиваем, что наиболее важными являются первые две стадии процесса, где действуют когерентные лазерные поля.

Будем исходить из уравнения Шредингера в форме , где по индексу m₁ производится суммирование по всем энергетическим состояниям атома, а матрица V_nm(t) определяется формулой (3.3.17) и более конкретно (30.2 ) и (30.3 ) Только теперь вместо одного поля у нас имеются два резонансных поля с амплитудами E₁ и E₂. Для трехуровневой системы с энергиями ₀, ₁ и ₂ (см. Рис. 3) из уравнения Шредингера стандартными методами записывается следующая система уравнений для амплитуд вероятностей а₀, а ₁ и а ₂ соответственно в виде:

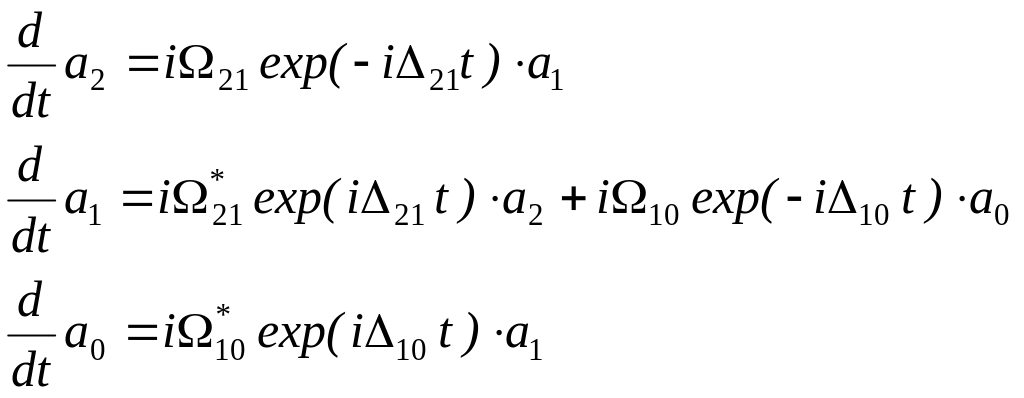(31.2)

где введены обозначения:

(31.3)

d₂₁ и d₁₀ есть характерные значения матрицы дипольных моментов атома между соответствующими состояниями и .

Для постоянных во времени (или достаточно медленных по сравнению с периодом лазерных монохроматических волн) амплитуд поля решение системы уравнений выполняется стандартными методами, поскольку заменами

a₂ = b₂ exp(-i ₂₁ t)

a₁ = b₁ (31.4)

a₀ =b₀ exp(i ₁₀ t)

система (31.2) преобразуется к системе уравнений с постоянными коэффициентами для нахождения искомых функций b₂, b₁ и b₀:

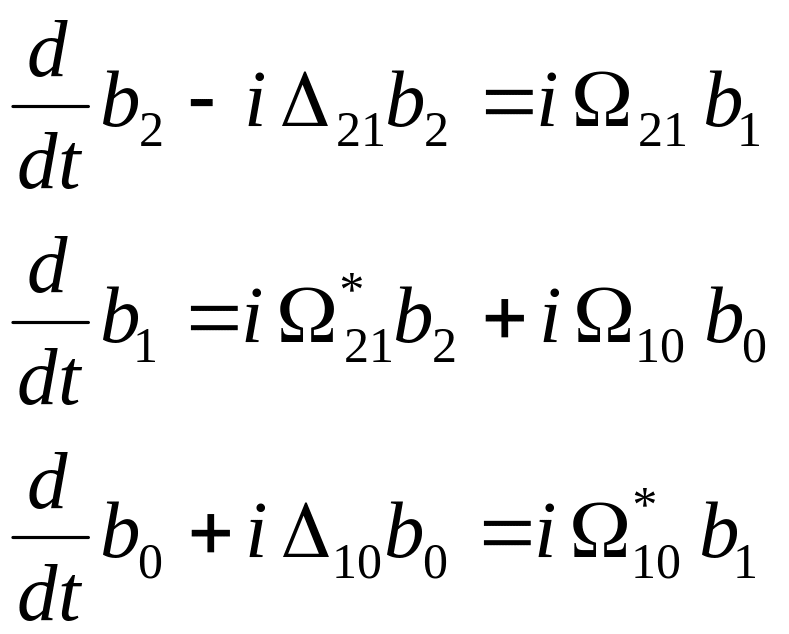(31.5)

Последняя преобразуется подстановкой b_j = B_jexp(-ixt) к системе однородных алгебраических уравнений

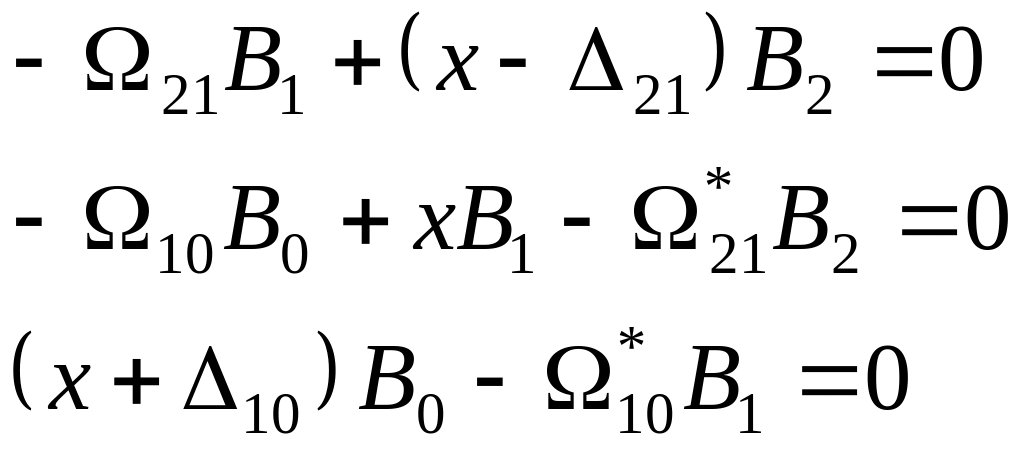(31.6)

Нетривиальное решение (31.6) существует, если ее детерминант равен нулю, т.е. в результате мы получаем для нахождения корней x₀, x₁, и x₂ алгебраическое уравнение третьей степени (кубическое):

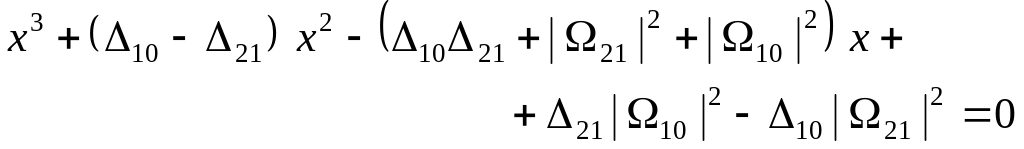(31.7)

Отсюда следует первый важный результат для системы (31.2): общее решение (31.2) и, соответственно, вероятность ₂ =  есть осциллирующая функция с угловыми частотами x₀, x₁, и x₂. Причем эти частоты в качестве корней уравнения (31.7) являются действительными величинами. Решение (31.7) можно выполнить, используя формулы Кардано или эквивалентное ему тригонометрическое решение.

Итак, общее решение (31.5) будет представлять есть суперпозиция осциллирующих экспонент exp (– ix_j t) с постоянными множителями. С учетом (31.4) то же самое справедливо для исходной системы уравнений (31.2). Например, общее решение для амплитуды вероятности а₂ уровня ₂ будет иметь вид:

a₂ = exp(–i ₂₁ t) (C₀ exp(ix₀ t)+ C₁exp(ix₁ t) + C₂exp(ix₂ t)) (31.8)

Используя связь а₀, а₁, и а₂ через уравнения (31.2)можно получить формулы для а₀ и а₁ в виде (31.8), которые мы не будем здесь выписывать. Далее, если мы примем следующие начальные условия:

a₀ (t = 0) = 1

a₁ (t = 0) = 0 (31.9)

a₂ (t = 0) = 0

которые соответствуют первоначальному нахождению атома в основном состоянии, то легко получаем систему неоднородных алгебраических уравнений для нахождения коэффициентов С₀, С₁, и С₂. В результате получаются следующие коэффициенты:

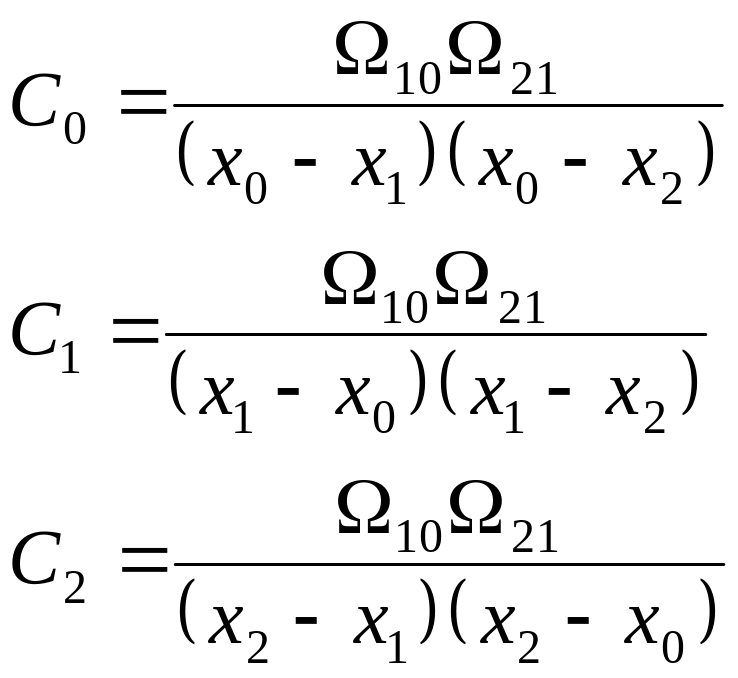(31.10)

Вид этих коэффициентов свидетельствует, что их числители одинаковы, а в знаменателе стоят два множителя в виде двучленов с разницей корней с легко запоминающейся структурой.

Таким образом, выражения (31.8) и (31.10) полностью определяют амплитуды а₀, а₁, и а₂, если найдены корни уравнения (31.7). Зная амплитуды, мы легко находим матрицу плотности _mn(t) в любой момент времени. Теперь мы можем добавить к найденным матричным элементам ₂₂, ₂₁, ₁₁, ₁₀, ₀₀ соответствующие релаксационные добавки. Этот путь нахождения матрицы плотности наиболее простой и краткий. Он пригоден и для более сложной, но конечной по состояниям квантовой системы.

Частные случаи для трехуровневой системы (аналитические решения).

1. ₁₀ = ₂₁ =0

В этом случае для произвольных значений ₁₀ и ₂₁ кубическое уравнение (31.7) имеет тривиальный вид: и его корни: x₀ = 0 и . Подставляя их в (31.10) можно далее найти, например

₂ = 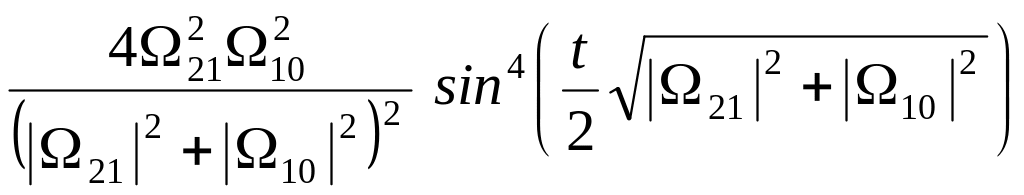 = (31.11)

Используя усреднение по времени, когда , получаем

(31.12)

при | ₁₀| = | ₂₁| имеем = 3/8. Таким образом, в максимально благоприятном случае, когда осуществляется точный резонанс на первых двух ступенях возбуждения, населенность уровня с энергией ₂, с которого производится фотоионизация, не превышает 3/8, тогда как в двухуровневом случае эффект насыщения дает 1/2. Анализ других уравнений показывает, что в этом случае =1/4, =3/8. Таким образом, на промежуточном уровне в условиях насыщения сохранится 25% атомов. На Рис. 4 показана зависимость от частот Раби | ₂₁| и | ₁₀|.

Рис. 4 Точный резо­нанс на обоих ре­зонансных перехо­дах и 2=21, 1=10. Зависимость усреденнной по вре­мени вероятности на уровне 2 от частоты Раби | 21| на втором пе­реходе при раз­личных частотах Раби | 10| для пер­вого перехода.

2. ₁₀ = ₂₁= ; ₁₀ = ₂₁ = .

Корни кубического уравнения (31.7) равны: x₀ = 0 и . Из (31.10) следует, что

; (31.13)

И для амплитуды вероятности а₂ получаем из (31.8):

(31.14)

и далее

(31.15)

Аналогично вычисляются усредненные по времени вероятности нахождения атома в состояниях и :

= ; = (31.16)

Заметим, что из (31.15) и (31.16) следует, что . При  = 0 мы получаем и , что совпадает с результатом в предыдущем разделе 1 ( = 0). В случае  >>  мы получим , и . Отсюда видно, что увеличение отстройки от резонанса существенно уменьшает населенность уровня ₂. Рис. 5 показывает графики , и как функции параметра r = .

Рис. 5 Усредненные вероятности , и при | 10| = | 21| =  и 10 = 21 =  в зависимости от параметра r = 2/2.

3. ₁₀ = ₂₁= ; ₁₀ = – ₂₁ = .

Кубическое уравнение (31.7) обладает в этом случае корнями: x₀ = 0 и , а коэффициенты (31.10) оказываются равными

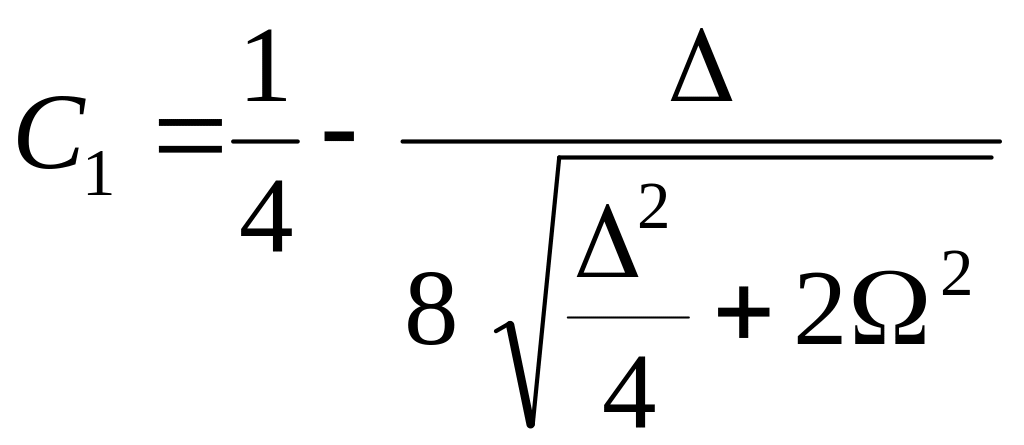; ; (31.17)

После подстановки (31.17) в (31.8) мы получим выражение

= (31.18)

где .

Численные результаты.

В общем случае необходимо решать кубическое уравнение (31.7), используя известные численные методики (см. приложение А). Затем рассчитать коэффициенты С₀, С₁, и С₂ в (31.10) и из (31.8) получить амплитуду а₂ в наивысшем возбужденном состоянии . Для оценки эффективности трехступенчатой фотоионизации достаточно вычислить усредненную по времени вероятность . При усреднении можно опустить осциллирующие слагаемые, так как они дают нулевой вклад. В этом приближении мы получим, что

(31.19)

Вероятность зависит, в самом общем случае, от четырех параметров: ₁₀, ₂₁, ₁₀, и ₂₁. Все эти аргументы имеют размерность угловой частоты (сек^-1). Выберем в качестве масштаба единицу гигигерц (10⁹ сек^-1). Эта величина соответствует значениям, характерным для АВЛИС метода (_D = 1,3 ГГц, _лаз = 1  4 ГГц). Оценим характерную частоту Раби для интенсивности лазерного излучения в 100 кВт/см². Напряженность (амплитуда) электричес­кого поля E₀ (для вида Е = 2E₀ cos t) и интенсивности лазерной волны I используем следующую связь:

E = 2E₀ = или E  30,6 , где [E ] = В/см [I] = Вт/см².

Для I = 10⁵ Вт/см² мы получаем E₀  510³ В/см. В качестве меры для дипольного момента перехода используем величину, равную одному дебаю (1 Д). При таком выборе частота Раби   410¹⁰ с^-1. Типичное значение дипольного момента для перехода (резонансный переход из основного состояния атома в первое возбужденное) есть 0,1 Д. Для второго перехода оно около 0,01 Д. Эти величины для интенсивностей 100 кВт/см² дают значение частот Раби  ~ 10⁹  10¹⁰ с^-1. Таким образом, в наших экспериментальных условиях частоты Раби при указанных интенсивностях лазерного излучения того же порядка, что и доплеровское уширение и ширина лазерного поля (примем во внимание, что  = 2 ~ 10¹⁵с^-1).

Удобно выбрать выражение для частоты Раби через интенсивность I , длину волны лазерного луча  и время жизни возбужденного состояния :

 = 0,7810⁵

где [] = сек, [] = мкм, [I ] = Вт/см², [] = с^-1.

Предыдущие теоретические выводы часто верны только при жестком условии  >> , где  – однородное (радиационное) уширение линии атомного перехода. Тем не менее их можно считать качественно верными и при  ~ . Далее следует принять во внимание, что теория рассматривает изолированный атом. Ее результаты могут быть обобщены на случай учета доплеровского уширения, если  ~ _D. Для этого достаточно усреднить результаты для изолированного атома по частотной отстройке  в соответствии с распределением Максвелла, а именно

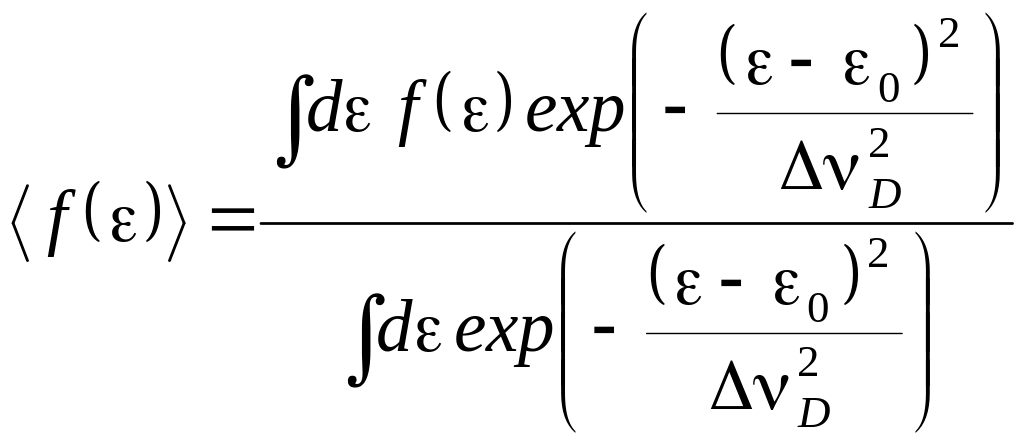
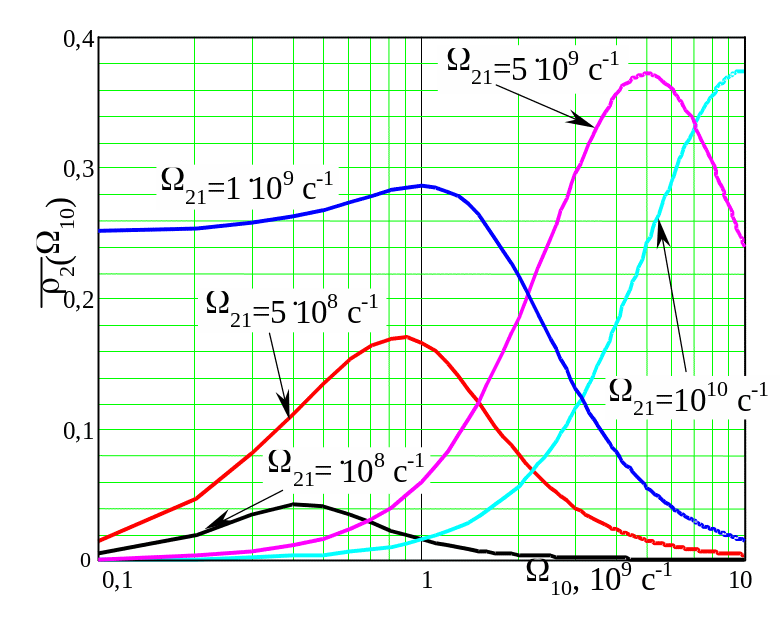
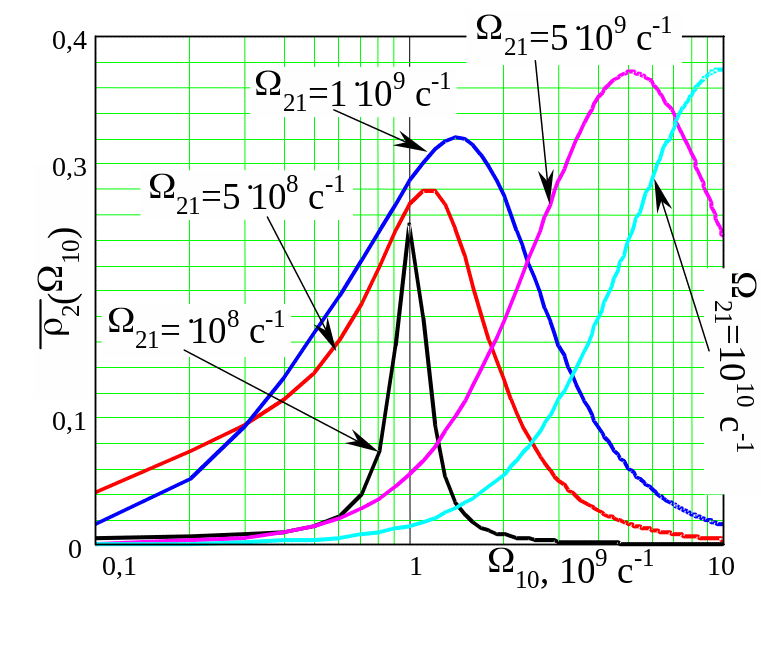
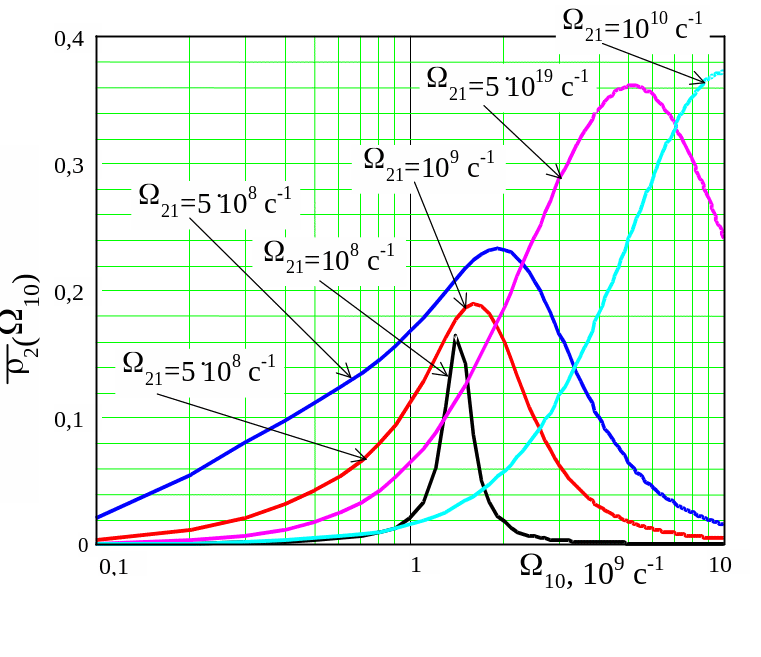
Численные расчеты показывают, что при ₂₁ = 0 и при ₁₀ = 110⁹ с^-1, а также при ₁₀ = 0 и при ₂₁ = 110⁹ с^-1 поведение как функции аргументов ₁₀ и ₂₁ качественно совпадает со случает точного резонанса (₂₁ = ₁₀ = 0). Это можно видеть из Рис. 6 и 7. Также отметим, что рост интенсивности лазерного излучения при таких когерентных взаимодействиях может приво­дить к уменьшению эффективности трехступенчатой ионизации. Поэтому надо стремиться выбирать оптимальную интенсивность.

a) Вероятность заселения верхнего уровня для различных величин частоты Раби на втором переходе.		б) Вероятности заселения уров­ней , и для случая сильной накачки на первом переходе и слабой на втором (21 << 10)

Рис. 6 Зависимости верятностей заселения уровней при различных соотношениях между частотами Раби ₁₀ и ₂₁ для случая точного резонанса по второй ступени (₁₀ = 110⁹ с^-1, ₂₁ = 0).

a) 10 = 1109 с-1, 21 = 0 (точный резонанс по второй ступени)			б) 21 = 1109 с-1, 10 = 0 (точный резонанс по первой ступени)

Рис. 7 Зависимость вероятности возбуждения верхнего уровня при различных соотношениях между частотами Раби ₁₀ и ₂₁ для случая точного резонанса по одной из ступеней.

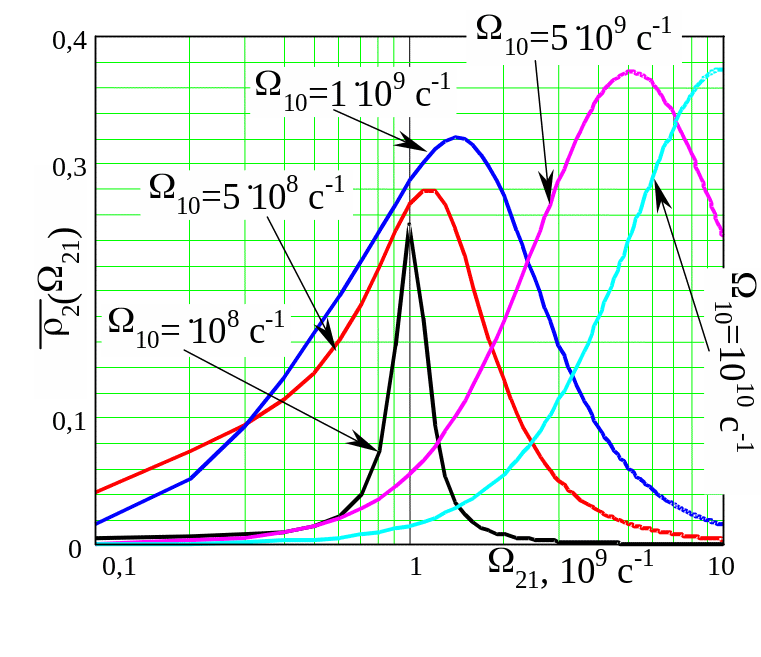
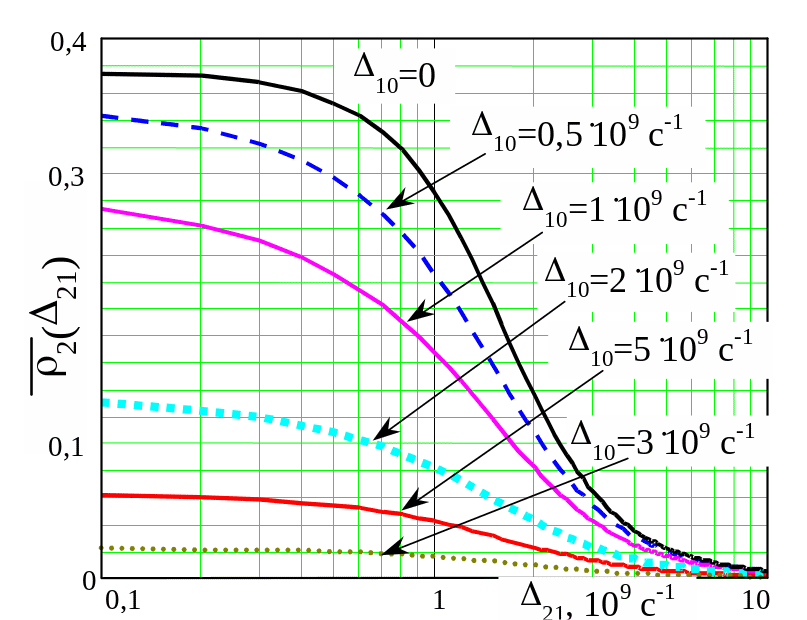
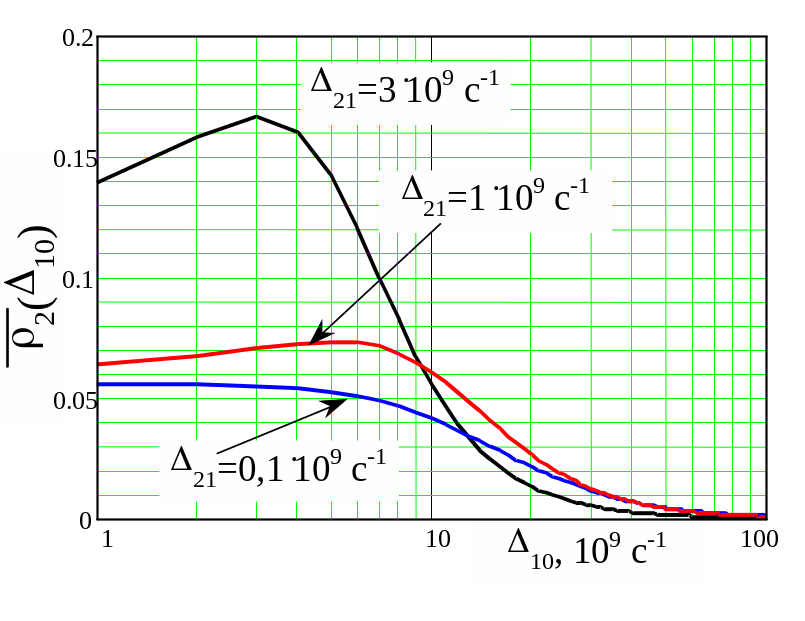
На Рис. 8 и 9 показана зависимость населенности уровня в зависимости от отстройки от резонансов ₁₀ и ₂₁. Увеличение отстройки на втором переходе в случае оптимальной накачки, когда ₁₀ = ₂₁ ведет к монотонному уменьшению . Естественно, что более предпочтительно использовать нулевую отстройку, т.е. ₂₁ = ₁₀ = 0.

a) При оптимальном соотношении интенсивностей возбуждения первой и второй ступеней 10 = 21=109 с-1			б) При 10 =5109 с-1 и 21=109 с-1.

Рис. 8 Зависимость вероятности возбуждения на верхний уровень от отстроек на первой (₁) и второй (₂) ступенях.

a) Равные отстройки 10 = 21			б) 10 = 10109 с-1, 21 = 1109 с-1

Рис. 9 Зависимости вероятности возбуждения на верхний уровень от отстроек ₁₀ и ₂₁ при различном соотношении частот Раби для первой и второй ступеней ₁₀ и ₂₁.

На Рис. 10, 11 показана зависимость селективности по изотопическому сдвигу на первой стадии возбуждения в схеме трехступенчатой ионизации. При этом второй переход находится в точном резонансе с излучением для обоих изотопов. Здесь также видно, что предпочтительно использовать нулевые отстройки.

Рис. 10 Зависимость се­лективности возбуж­де­ния в трехступенчатой схеме ионизации от изотопического сдвига на первой ступени (вто­рой переход нахо­дится в точ­ном резо­нансе с излуче­нием для обоих изотопов) при различ­ных соот­ноше­ниях между 10 и 21

Рис. 11 Зависимость селективности возбуж­дения в трехступенча­той схеме ионизации от величины изо­топи­ческого сдвига для случая одинаковых изотопических сдви­гов на первой и второй ступенях 1=2= при различных соотно­шени­ях между часто­тами Раби 10 и 21

Учет релаксационных членов и их влияние на эффективность трехступенчатой фотоионизации см. в приложении II.

.

Приложение I .

Кубические уравнения.

[Г.Корн, Т.Корн Справочник по математике. М., "Наука", 1977 ]

1. Решение Кордано.

Уравнение x³+ax²+bx+c=0 подстановкой x = y – a/3 приводится к виду

y³ + py + q = 0, p = -a²/3 + b, q=2(a/3)³ - ab/3 + c, (1)

корни которого

y₁ = A + B, y_2,3 = – (A+B)/2 i (A+B)/2,

где A= , B= , , A и B – любые кубичные корни, удовлетворяющие соотношению AB = –p/3.

2. Тригонометрическое решение.

Если уравнение (1) имеет действительные коэффициенты, то:

a) При

где

b) При

где

c) При

где

Всюду берется действительное значение кубичного корня.

Приложение II.

Уравнения для матрицы плотности в трехуровневой модели фотоионизации.

Процедура вывода уравнений для матрицы плотности та же самая, что и в случае двухуровневой модели. В этом случае по аналогии с выводом системы (30.1 а,б,в) система уравнений имеет следующий исходный вид:

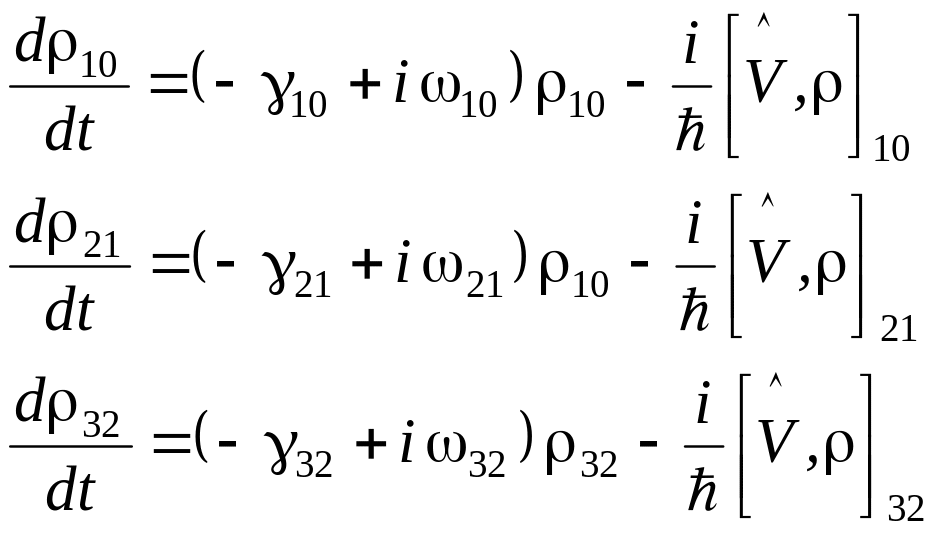(1)

где ₁₀, ₂₁, ₃₂ есть константы релаксации недиагональных элементов матрицы плотности, описывающих квантовые корреляции между состояниями , , и в соответствии с (3.3.48) напомним, что , , . Далее, для диагональных элементов матрицы плотности получаем, что

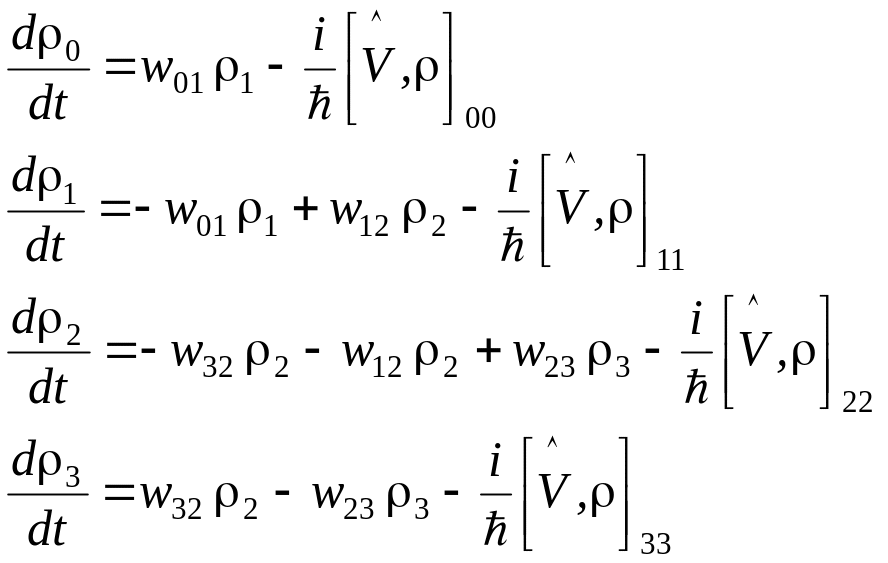(2)

где все вероятности w_nm означают вероятность переходов из состояния в состояние . В эти же уравнения для ₀, ₁, ₂ и ₃ можно добавлять различные дополнительные процессы, например, уход и приход в определенные состояния атома с метастабильных состояний или подобного типа. Коммутаторы , входящие во все вышеприведенные выражения в этом разделе, вычисляются так же как и в разделе А в формулах (30.5):

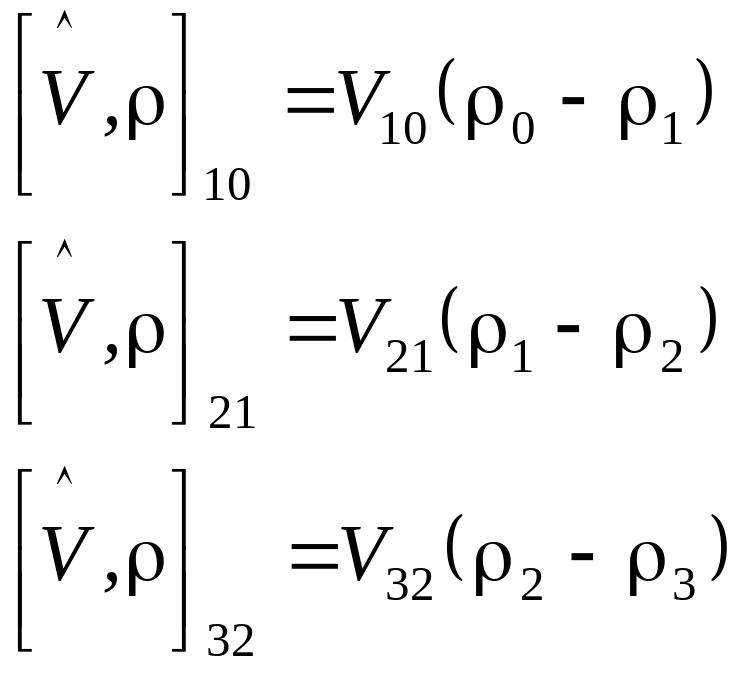(3)

(4)

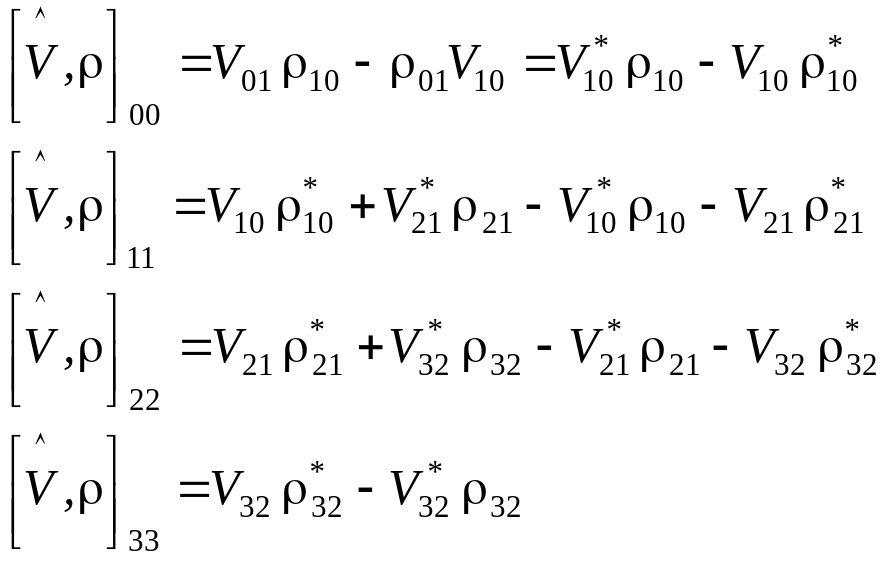
Здесь использованы соотношения и . Полученные выше коммутаторы подставляются в соответствующие уравнения для матрицы плотности, а матричные элементы V_nm раскрываются по формуле (30.3) с использованием обозначений, принятых при выводе выражения (30.4), где  приравнивается соответствующей переходу частоте ₁, ₂ или ₃.

Итак, выпишем необходимые для дальнейшего виды матричных элементов V₁₀, V₂₁ и V₃₂, входящие в вышеприведенные выражения:

(5)

где использованы обозначения: ₁₀ =  , ₂₁ =  , ₃₂ =  , при этом , , (в отличие от формулы (30.3) здесь в определения частот переходов Раби ₁₀, ₂₁ и ₃₂ входит коэффициент 1/2).

Для недиагональных элементов матрицы плотности решение уравнений ищем в том же виде, что и (30.6), т.е. _mn = _mn exp (–i_ t) где _ =(₁, ₂, ₃) для соответствующего резонанса, т.е. ₁₀ = ₁₀ exp (–i₁ t), ₂₁ = ₂₁exp (–i₂ t), ₃₂ = ₃₂ exp (–i₃ t).

Подставляя последнее выражение в систему уравнений (1) и отбрасывая быстропеременные слагаемые, содержащие удвоенные частоты осцилляций, получим, что

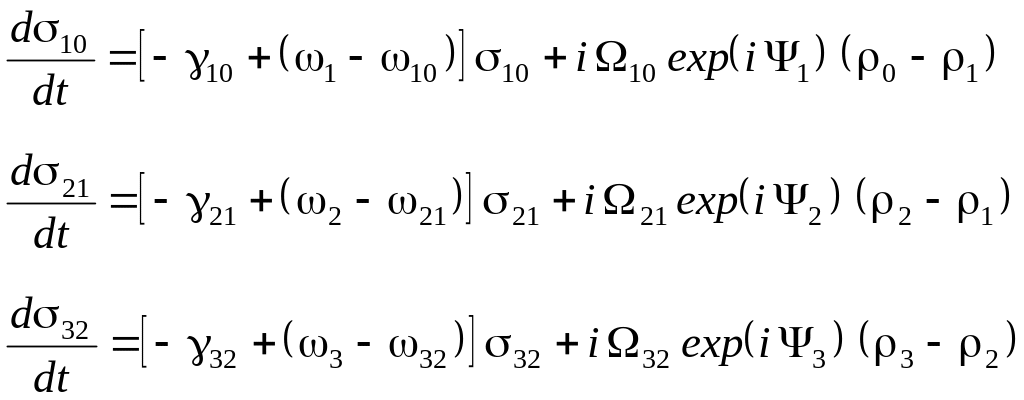(6)

где ₁ = k₁ r + ₁, ₂ = k₂ r + ₂ и ₃ = k₃ r + ₃.

Сравнивая (6) с уравнениями (30.7), мы видим, что они ему аналогичны по форме, за исключением последнего слагаемого в (30.7), который был отброшен во всех уравнениях (5). Далее введем обозначения ₁₀ = ₁ – ₁₀, ₂₁ = ₂ – ₂₁, ₃₂ = ₃ – ₃₂. Поэтому по аналогии с (30.10) получаем

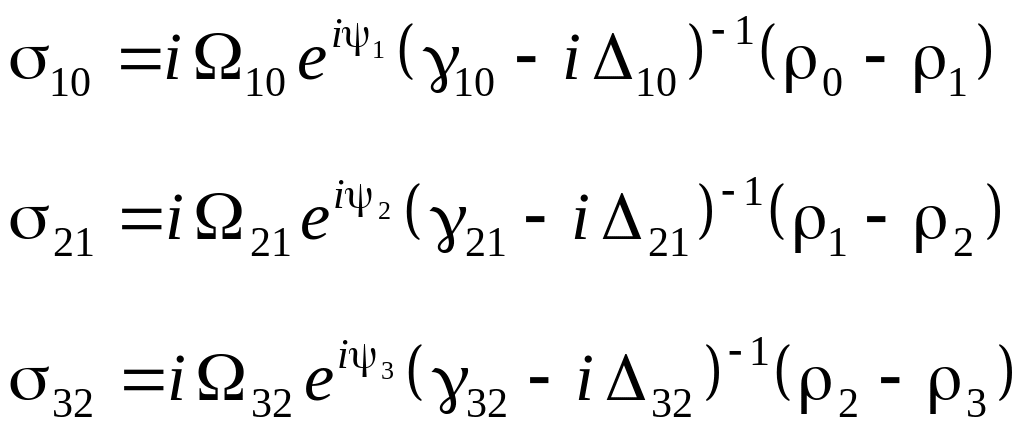(7)

которые справедливы для быстрой релаксации, т.е. при ₁₀ >> , ₂₁ >> и ₃₂ >>

Опуская быстропеременные слагаемые в уравнениях для диагональных элементов матрицы плотности, приходим окончательно к следующей исходной системе уравнений, пригодной для численного счета:

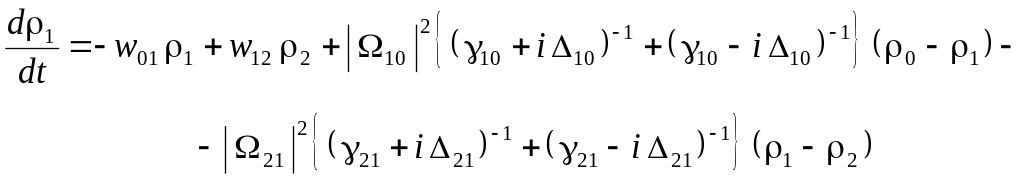
(8)

Полученная система имеет простой физический смысл: в каждое состояние есть приход или уход или и то и другое за счет термостата (вероятности w_mn) и за счет внешнего лазерного поля (вынужденные переходы). Выражение в фигурных скобках в каждом уравнении есть действительная величина, равная

(9)

которая учитывает частотную расстройку при резонансных переходах. Квадраты частот Раби пропорциональны интенсивностям соответствующих лазерных полей. В представленной форме уравнения для матрицы плотности (8) эквивалентны кинетическим (балансовым) уравнениям при статистическом подходе к проблеме фотоионизации. В этих уравнениях при строгом резонансе ( = 0) нельзя сделать переход к чисто когерентному взаимодействию, так как при   0 выражение {   } расходится.

В более компактном виде систему уравнений (8) можно представить, если ввести обозначение (по аналогии с формулой (30.11 в)

(10)

С учетом (9) и (10) система уравнений преобразуется к окончательному виду (для сравнения см. также формулу (30.12 б)):

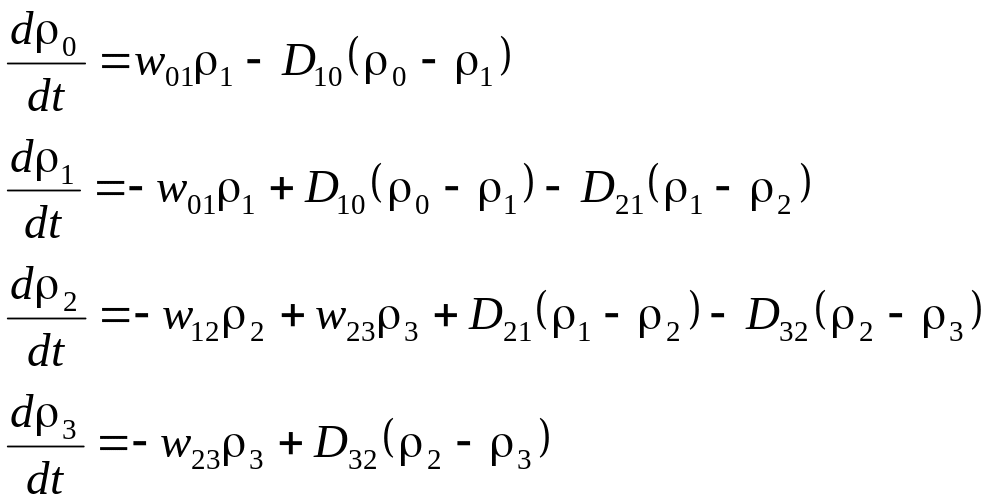(11)

Аналогично можно составлять уравнения для многоуровневых систем с учетом всевозможных переходов.

Если релаксационные процессы того же порядка, что и соответствующие частоты Раби, т.е ₁₀ ~  ,₂₁ ~  и ₃₂ ~  , то в этом случае решения в виде (7) и уравнения (8) непригодны для анализа. Необходимо обратиться к системе исходных уравнений для  (6), присоединяя к ним систему уравнений для диагональных элементов (2) с учетом формул (4) и (5). Формулы (4) с учетом отброшенных быстропеременных во времени слагаемых (с удвоенными частотами) примут следующий вид:

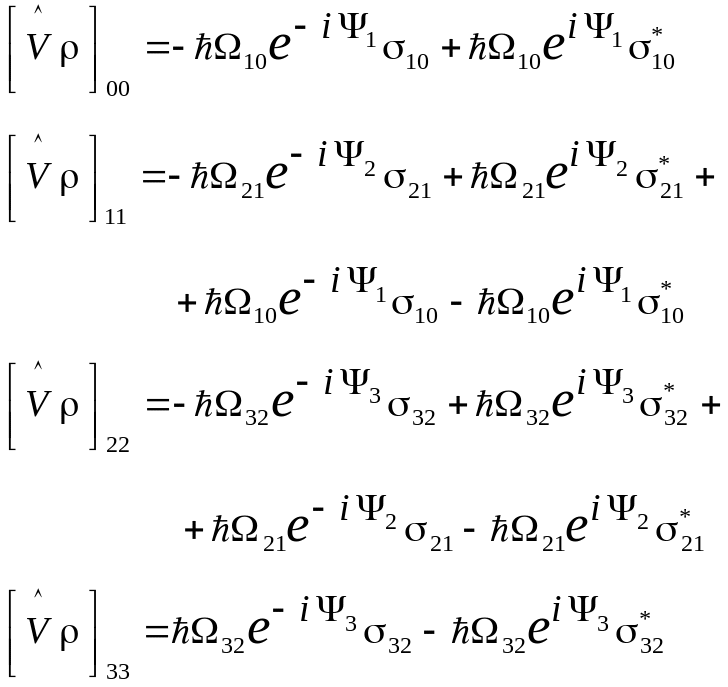(12)

Итак, система (2) с учетом (12) и система (6) полностью определяют систему уравнений для трехуровневой модели фотоионизации при произвольных параметрах релаксации, частот Раби и малых отстроек.

ПРИЛОЖЕНИЕ III