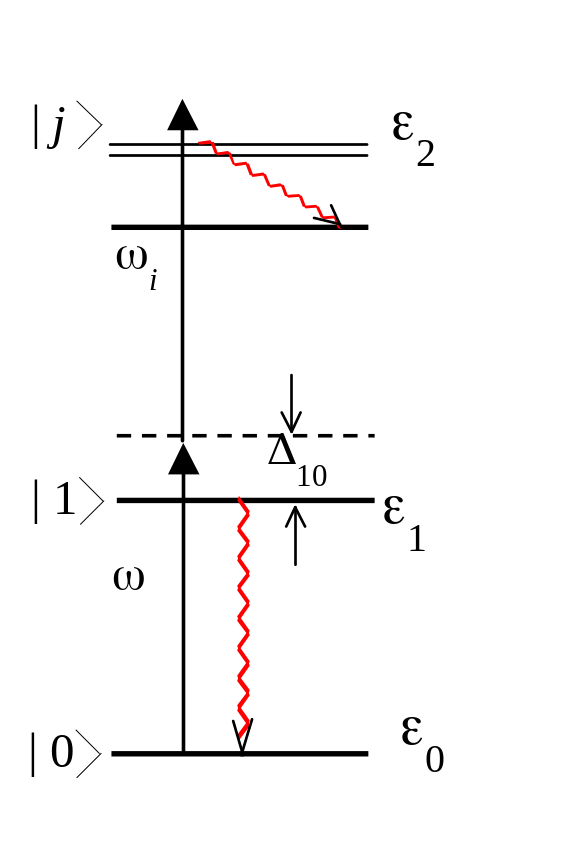§ 30. Модель двухуровневой системы для фотоионизации

Рассмотрим следующую систему уровней атома Рис. 2

Рис. 2 Двухступеньчатая ионизация.

Уравнения для матрицы плотности (29.7) в этом случае примут вид: (30.1 а) (30.1 б) (30.1в)

Полагаем, что дополнительно с уровня ₁ на уровень ₂ происходит процесс возбуждения с вероятностью w_j1. Фотоионизация осуществляется через автоионизационное состояние со скоростью w_j2, значительно превышающей скорость возбуждения, т.е. w_j1 << w_j2.

Сначала предположим, что вероятность второй ступени (фотоионизации) ничтожно мала по сравнению со скоростью перехода между первым состоянием и основным состоянием , т.е. w₁₀ >> w_j1. Допустим, что разница ₁₀ =  – ₁₀ (т.н. отстройка частоты оптической волны  от частоты атомного перехода) много меньше  и ₁₀.

Из уравнения (26.3) следует, что оператор взаимодействия лазерных волн с веществом имеет вид . Лазерные поля являются плоскими монохроматическими волнами в соответствии с (26.5). Оператор взаимодействия для одной волны с частотой  состоит из двух слагаемых:

(30.2)

Здесь мы ограничились одной компонентой вектора электрического поля и одной компонентой оператора дипольного момента , где ⁺ есть эрмитово сопряженный с : (d ⁺)_nm =  . В общем виде матричный элемент оператора (30.2) также состоит из двух слагаемых

(30. 3)

Для двухуровневой системы между состояниями и достаточно ограничиться равными друг другу двумя матричными элементами V₁₀, :

= =

(30.4)

где мы ввели новое обозначение ₁₀ =  , совпадающее с частотой Раби. При этом . Как видно из (30.4) в этом конкретном случае V₁₀ = V₀₁. Для двухуровневой системы коммутаторы, входящие в (30.1), имеют простой вид:

(30.5)

Заметим, что и . Подставим (30.5) в уравнения (30.1), получим, что

(30.5 а)

и поскольку диагональные элементы матрицы плотности ₀ и ₁ входят в (30.5 а) в виде разницы, то составим из (30.5 б) и (30.5 в) уравнение для ₀ – ₁:

(30.5 б)

где мы ввели время (для инфракрасного диапазона).

В оптическом диапазоне при температурах меньше 10⁴ К можно пренебречь спонтанными переходами из основного состояния в возбужденные, то есть считать что w₁₀ = 0 в соответствующих формулах (30.5 б) и (30.5 в). В этом случае удобно записать непосредственно уравнения для ₀ и ₁ отдельно, именно

(30.5 в)

Заметим, что уравнение для разницы (₀ – ₁) будет иметь вид (30.5 б), где в правой части вместо релаксационного слагаемого появится слагаемое (см. также (30.9)).

Будем искать решение уравнения (30.5 а) в виде

(30.6)

Подставим (30.6) и (30.3) в уравнение (30.5 а), которое преобразуется к виду

(30.7)

где  = .

Это дифференциальное уравнение имеет точное решение, именно:

(30.8)

где . Решение (30.8) часто используют для численных расчетов.

Уравнение (30.5 б) с использованием выражений (30.3) для V₁₀ и (30.6) преобразуется к виду

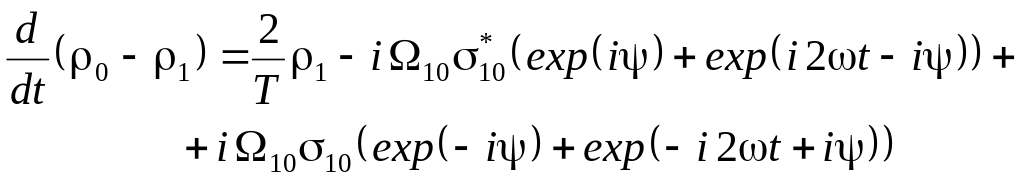(30.9)

Здесь учтено, что в оптическом диапазоне из возбужденного состояния есть переход в основное состояние , тогда как обратный переход из  под действием термостата отсутствует. Кроме того, ₀ + ₁ = 1 (или N – число частиц в единице объема).

Следует отметить, что в уравнении (30.7) для ₁₀(t) и (30.9) для (₀ – ₁) некоторые члены являются быстропеременными, в то время как другие – медленноменяющимися по сравнению с частотами  и ₁₀. В первом приближении быстропеременные слагаемые, которые содержат временной фазовый множитель , можно не учитывать. Более точный их учет можно сделать методом последовательных приближений, и он приводит к сдвигу атомной частоты ₁₀, т.е. к так называемому штарковскому сдвигу, которым в большинстве практических случаев при однофотонном резонансе, как здесь рассматривается, можно пренебречь. Кроме того, за счет быстрой релаксации фазовой памяти, обычно в (30.7) опускают левое слагаемое, т.е. производную по времени:  = 0. С этими оговорками, решение (30.7) запишется следующим образом

(30.10)

Сначала рассмотрим случай инфракрасного диапазона. Подставляя (30.10) в (30.6), а последнее в (30.5 б) и опуская быстропеременные во времени слагаемые, получим следующее уравнение для разницы населенностей в виде экспоненциального закона:

; (30.11 а)

где введены обозначения

D = (30.11 б)

D₁₀ = 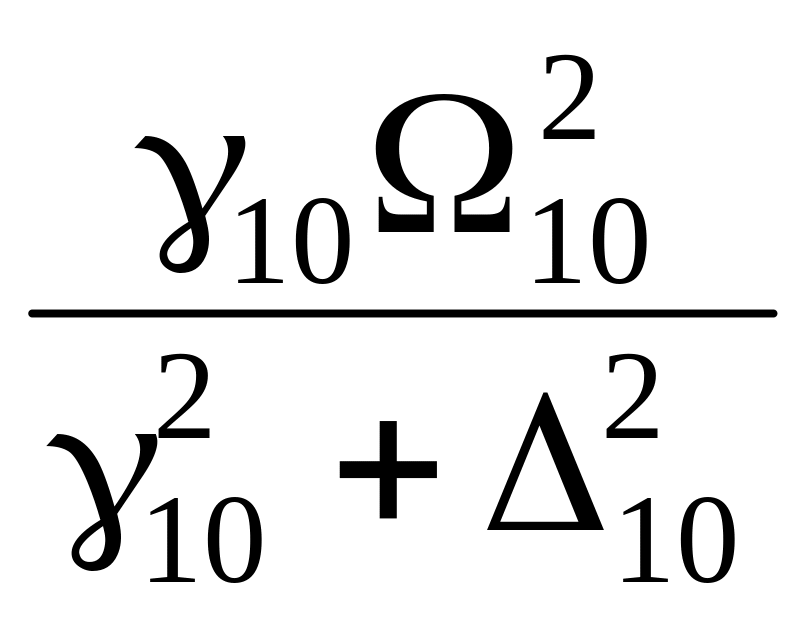(30.11 в)

здесь ₁₀ =  – ₁₀ =  –  (₁ – ₀),

которое должно быть решено при начальных условиях ₀(0) = N, ₁(0) = 0.

С учетом нормировки матрицы плотности на концентрацию атомов N в единице объема (₀ + ₁ = N) получаем следующее окончательное решение

(30.11 г)

Теперь обратимся к случаю оптического диапазона. Подставляя выражение (30.10) в формулу (30.6), а последнюю в систему уравнений (30.5 в), с учетом (3.3.53) нетрудно преобразовать эту систему к более наглядному виду:

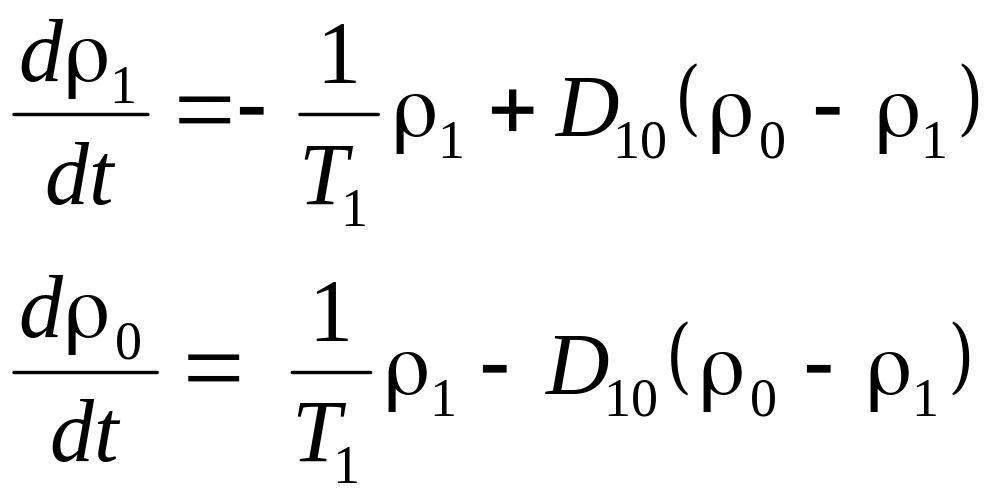(30.12 а)

При выводе системы уравнений (30.12 а) были опущены слагаемые, содержащие множитель exp( i 2t). В данном случае (как и при выводе уравнения (30.11 а)) это пренебрежение быстропеременными во времени слагаемыми эквивалентно усреднению этих уравнений по времени (обычно – по периоду колебаний лазерного поля Т = 2/). Входящие в рассматриваемые уравнения (30.11 а) и (30.12 а) искомые ₀(t) и ₁(t) являются медленно­меняющимися функциями времени с характерным временем t_хар ~ D^‑1.

Для тех же начальных условий, что и ранее (₀(0) = N, ₁(0) = 0) решение системы уравнений(30.12 а) имеет следующий вид:

(3.3.12 б)

Из общего вида решений (30.11 г) для инфракрасного диапазона и (30.12 б) для оптического диапазона хорошо видно, что качественно временнáя зависимость носит экспоненциальный характер. При условии, что D₁₀T₁ << 1 влиянием оптического поля можно пренебречь. В противоположном случае сильного поля при условии D₁₀T₁ >> 1 влияние поля весьма существенно, при этом с течением времени населенности выравниваются:₀  N/2, ₁  N/2, (эффект насыщения).

Более точный расчет с учетом влияния отброшенных быстропеременных слагаемых в уравнениях (30.7) и (30.9) был выполнен в [1]. Основные уравнения, применимые к рассматриваемой двухуровневой модели, остаются по форме те же самые. Однако вместо частоты атомного перехода ₁₀ в формулах (30.7), (30.9) и (30.10) необходимо сделать замену на ₁₀ + _s, где дополнительное слагаемое _s (сдвиг атомной частоты) квадратично зависит от электрического поля лазерной волны

_s =  (30.13)

Иногда эта величина называется динамическим штарковским сдвигом. Коэффициент  определяется следующей формулой:

= (30.14)

Здесь суммирование по n производится по нерезонансным состояниям, т.е. n  0 и n  1. Отметим, что даже для двухуровневой системы, когда отсутствуют нерезонансные состояния также существует штарковский сдвиг за счет первого слагаемого в (30.14). Подчеркнем, что выражение для _s остается справедливым и в когерентном случае взаимодействия лазерного поля со средой, когда полностью исключается механизм релаксации.