§ 25. Кинетические уравнения при фотоионизации оптически тонкого слоя.
В этом параграфе представлена процедура решения системы скоростных уравнений из предыдущего параграфа в случае строгого резонанса. Отклонение от резонанса рассматривается далее в §26. Аналитическое решение удается найти при следующих предположениях: 1) двухфотонное поглощение несущественно 2) световые пучки однородны по интенсивности в пространстве и во времени (т.е. импульсы лазерного излучения – прямоугольные).
Система трех уравнений (24.2), (24.5) и (24.6) без учета двухфотонного поглощения имеет следующий вид:
(25.1)
В принятых предположениях система уравнений (25.1) содержит только постоянные коэффициенты в правых частях. Общее решение подобных обыкновенных линейных дифференциальных уравнений представляется в виде суммы экспоненциальных функций exp( t). Например, общее решение для 3(t) можно записать в виде:
(25.2)
где Р находятся из конкретных начальных условий. Общий вид решения для 2(t) легко находится, если подставить (25.2) в первое уравнение системы (25.1). Получим, что
(25.3)
Здесь и далее, ради простоты, считается, что W23 = W32 = W2, W21 = W12 = W1 и Wi3 = W3, А23 = А2, А12 = А1. В этих же обозначениях и при подстановке 3(t) в виде (25.2) и 2(t) в виде (25.3) во второе уравнение системы (25.1) находим общий вид для 1(t):
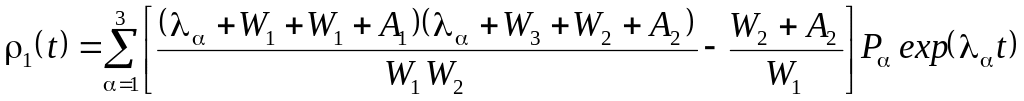(25.4)
Таким образом, общее решение системы трех уравнений (25.1) определяется формулами (25.2) – (25.4) через коэффициенты P и корни характеристического уравнения, которое для данной системы линейных дифференциальных уравнений сводится к нулю детерминанта третьего ранга:
= 0 (25.5)
или, после раскрытия этого детерминанта по известным правилам получаем вместо (25.5) кубическое относительно алгебраическое уравнение:
( + W3 + W2 + A2)( + W2 + W1 + A1)( + W1) –
– ( + W1)W2(W2 + A2) – ( + W3 + W2 + A2)W1(W1 + A1) = 0 (25.6)
В приложении Б к этой главе содержатся два аналитических метода нахождения корней произвольного кубического уравнения.
Наиболее важным является состояние , которое первоначально находится в основном состоянии с энергией 1. Поэтому положим в качестве начальных условий следующие:
1(t0) = 0
2(t0) = 0 (25.7)
3(t0) = 0
где 0 есть исходная концентрация атомов выделяемого изотопа. Далее, опуская выкладки по нахождению коэффициентов Р и подставляя формулу (25.2) в интеграл (24.7) получим выражение для концентрации фотоионов (или, в данном случае, и для фотоэлектронов) для i(t) в следующем виде (для упрощения вида конечного выражения положим t0 = 0):
(25.8)
где коэффициент Z определяется формулой:
Z = [(1 + W3 + W2 + A2)(1 + W2 + W1 + A1) – W2 (W2 + A2)] (2 – 3) + + [(2 + W3 + W2 + A2)(2 + W2 + W1 + A1) – W2 (W2 + A2)] (3 – 1) + + [(3 + W3 + W2 + A2)(3 + W2 + W1 + A1) – W2 (W2 + A2)] (1 – 2)
|
(25.9) |
Из (25.8) и (25.9) видно, что структура слагаемых в них обладает своеобразной циклической симметрией: каждое слагаемое совпадает с последующим за ним в результате циклической перестановки корней, т.е. 1 2 3 1 2 … и т.д. Видно также, что временнáя зависимость i(t) определяется тремя экспонентами с показателями t, где = 1, 2, 3.
В качестве примера рассмотрим предельный случай, когда существует мощное лазерное излучение на первой и второй ступени возбуждения. Предположим, что вероятность индуцированных переходов много больше вероятности спонтанных переходов. С другой стороны, будем также считать, что вероятность фотоионизации с верхнего возбужденного состояния мала в сравнении с индуцированными переходами. В этом случае система трех уравнений (25.1) сильно упрощается, именно:
(25.10)
и характеристическое уравнение (25.5) в форме кубического (25.6) имеет вид:
3 +22 (W1 + W2) + 3 W1 W2) = 0 (25.11)
которое обладает корнями
1 = 0 2,3 = –(W1 + W2) 
(25.12)
Нулевой корень преобразует первое слагаемое в формуле для концентрации фотоионов (3.2.14) к линейной зависимости от времени:
=
=
= (25.13)
=
Два других корня имеют отрицательные значения и поэтому сумма двух последних слагаемых в (25.8) с течением времени стремится к стационарному значению.
Для большей наглядности выпишем концентрации атомов на дискретных уровнях для случая, когда интенсивности лазерных полей подбираются таким образом, чтобы скорости переходов на первой и второй ступени возбуждения были бы равны (W1 = W2 = W). В этом случае система уравнений (25.10) становится однопараметрической:
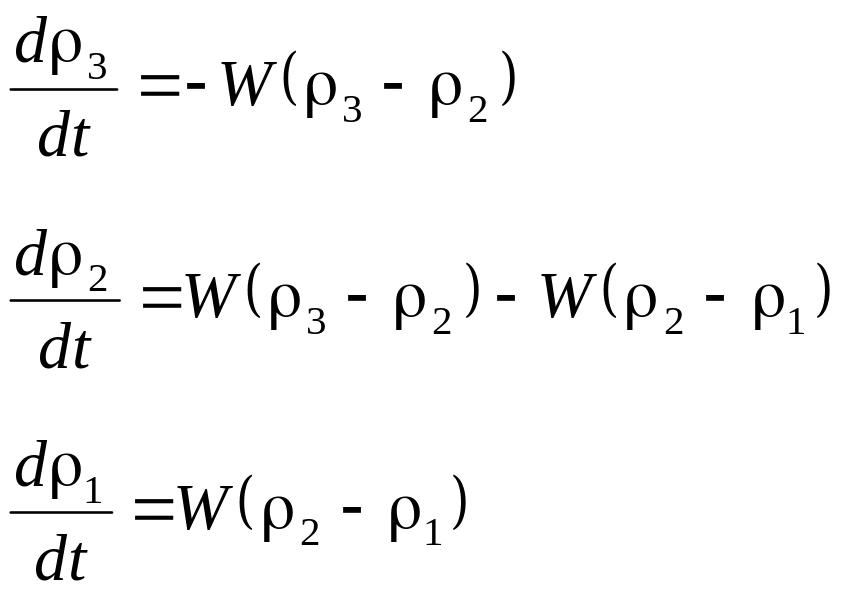(25.14)
а формулы (25.2) – (3.2.4) для начальных условий (25.7) преобразуются к простому виду:
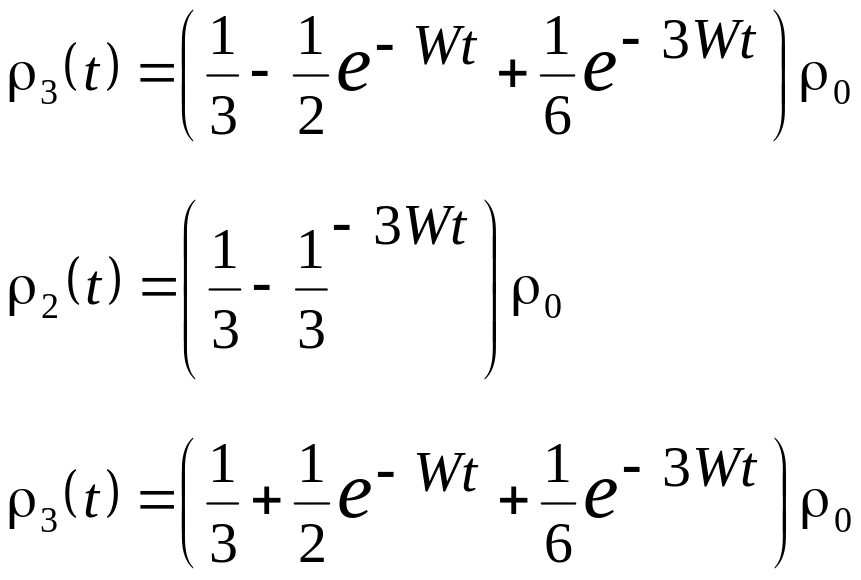(25.15)
Видно, что при t населенность уровней стремится к стационарному значению по 1/3 в каждом состоянии , и . Заметим, что этот результат справедлив только для некогерентного взаимодействия лазерного излучения с веществом. В следующем §26 этой главы будут рассмотрены следствия когерентного взаимодействия на основе формализма матрицы плотности, где населенность рассматриваемых уровней иная.