Глава V. Фотоионизация лазерным излучением

§ 24. Трехступеньчатая фотоионизация в сильном лазерном поле

Если лазерное излучение есть полностью некогерентное световое поле, то для построения теории фотоионизации можно пренебречь фазой и фиксировать только число фотонов в импульсе (или выражать интенсивность через число фотонов). Этот статистический подход позволяет значительно упростить общую задачу, требующую рассмотрения системы уравнений для матрицы плотности трехуровневого атома, и ограничиться уравнениями баланса (скоростными уравнениями).

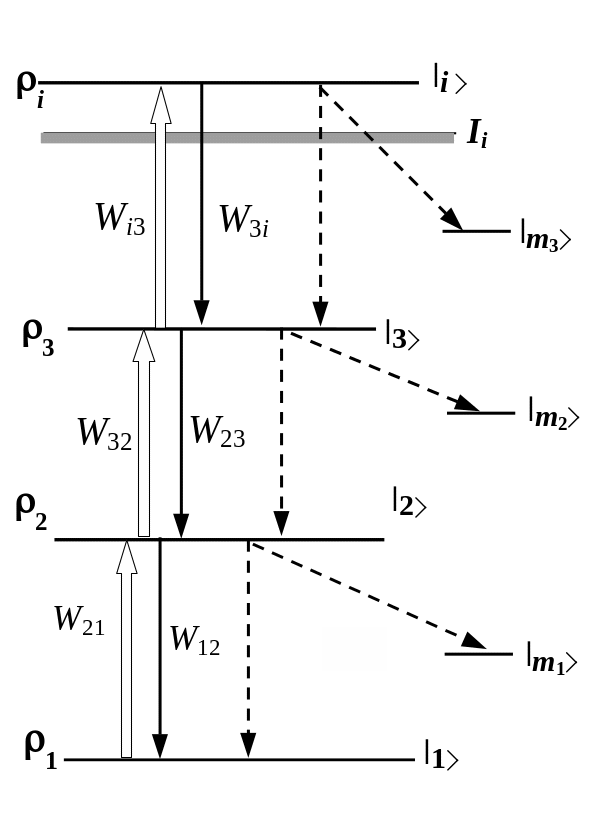
В этом параграфе представлены кинетические уравнения для трехступенчатой фотоионизации атомов в лазерном некогерентном поле. На Рис. 7 показаны дискретные уровни энергии атома с населенностями ₁, ₂, ₃

Рис.1 Схема трехступенчатой фотоионизации. Здесь 1, 2, 3 и i есть населенности уровней 1, 2, 3 и i (1 – энергия основного состояния атома, 2 и 3– энергии его возбужденных состояний, i – энергия автоионизационного уровня). Обозначения , , и соответствуют вышеуказанным энергиям и описывают квантовые состояния атома

с энергиями ₁, ₂, ₃ в состояниях: – основное состояние, – первое возбужденное состояние, – верхнее возбужденное состояние. Кроме того, состояние обозначает автоионизационное состояние, расположенное выше потенциала ионизации I_i. Сплошными линиями обозначены индуцированные (вынужденные) переходы под действием некогерентного лазерного излучения. Скорость вероятности таких переходов из состояния в состояние определяется величиной W_ba = Ф_ba _ba, где Ф_ba есть плотность потока фотонов с энергией , резонансных переходу  , а _ba – сечение возбуждения соответствующего перехода. Отметим, что исполь­зуются следующие размерности этих величин: [W_ba] = с^-1; [Ф_ba] = см^-2 с^-1; [_ba] = см². Вертикальные стрелки, направленные вверх, указывают на процессы возбуждения, направленные вниз – на процессы вынужденного испускания. Штрихованными линиями обозначены спонтанные переходы на соответствующие уровни, а также переходы на возможные метастабильные (долгоживущие) состояния , если таковые будут присутствовать и сильно влиять на процессы фотоионизации. Фотоэлектрон, который возникает на уровне _i автоионизационного состояния, довольно быстро (по сравнению с временами жизни электронов в дискретных состояниях ₁ и ₂) переходит в непрерывный спектр и далее вносит вклад в электронную составляющую ионизационного тока под действием постоянного поля в объеме ионизационной камеры. По этой причине часто можно пренебречь обратным индуцированным переходом W_3i. В этом случае изменение концентрации (населенности) электронов на уровне _i происходит за счет прямых переходов с уровня ₃. Пренебрегая первоначально процессами обратными (т.е. процессами распада), получим уравнение баланса, имеющее простейший вид:

(24.1)

Для нижележащих дискретных уровней вплоть до основного состояния следует отметить, что изменение концентрации (населенности) на этих уровнях существенно зависит от интенсивности световых, лазерных источников излучения, т.е. от плотности потока резонансных фотонов. Населенности этих уровней могут быть сравнимы друг с другом по порядку величины, так что необходимо тщательно и конкретно учитывать все прямые и обратные переходы в уравнениях баланса. Например, концентрация возбуж­денных атомов на уровне ₃ определяется скоростным уравнением вида:

(24.2)

Здесь первое слагаемое в правой части уравнения (24.2) содержит скорость индуцированного перехода на автоионизационный уровень, т.е. скорость перехода в непрерывный спектр (слагаемое – W_i3 ₃), а также "уход" на нижний уровень с энергией ₂ за счет вынужденного и спонтанного переходов (слагаемые – W₂₃ ₃ и – А₂₃ ₃), где А₂₃ = 1/₂₃, ₂₃ – время спонтанного распада состояния при переходе в состояние . Слагаемое +W₃₂ ₂ в (24.2) описывает "приход" атомов в состояние с энергией ₃ при индуцированном возбуждении лучом лазера, резонансным переходу  .

Здесь следует отметить, что иногда необходимо учесть процессы двухфотонных переходов из основного состояния в возбужденное состояние . Двухфотонный переход  соответствует одновремен­ному поглощению двух фотонов ₁+ ₂, где ₁ и ₂ – частоты лазерных лучей первой и второй ступеней возбуждения. В этом случае необходимо добавить в правую сторону уравнения (24.2) с положительным знаком слагаемое вида

+ (₃₁Ф₃₂Ф₂₁) ₁ (24.3)

где выражение в скобках соответствует скорости двухфотонных переходов  . Слагаемое (24.3) является "приходом" атомов в состояние с энергией ₃ при индуцированном возбуждении двумя лазерными лучами, находящимися в двухфотонном резонансе ₁+ ₂= ₃ – ₁.

Аналогичным образом необходимо в (24.2) учесть "уход" атомов за счет обратного индуцированного двухфотонного перехода. В отличие (3.2.3) при переходе  в (24.2) появляется слагаемое с отрицательным знаком вида

– (₁₃Ф₃₂Ф₂₁) ₃ (24.4)

где выражение в скобках соответствует скорости обратных индуцированных двухфотонных переходов  . Подчеркнем, что коэффициенты ₃₁ и ₁₃ в общем случае не обязательно равны друг другу!

При частотах ₁ и ₂, находящихся в строгом резонансе со своими атомными частотами переходов, вклады (24.3) и (24.4) в уравнение (24.2) в широкой области значений интенсивностей используемых лазерных излучений весьма малы и ими почти всегда можно пренебречь. Однако, если имеется расстройка между частотами лазерных волн и частотами атомных переходов, то двухфотонные переходы необходимо учитывать как в уравнении (24.2), так и в приводимом далее уравнении (24.6).

Аналогичный подход к определению концентраций атомов ₂ и ₁ на уровнях ₂ и ₁ соответственно приводит к уравнениям похожего вида, именно:

(24.5)

(24.6)

В уравнении (3.2.5) первое слагаемое в правой части описывает "уход" атомов с уровня ₂ за счет индуцированных и спонтанных переходов в состояния и ; остальные слагаемые есть "приход" из и за счет соответствующих переходов. В уравнении (24.6) слагаемые имеют ту же интерпретацию с той лишь разницей, что последние слагаемые учитывают двухфотонные переходы, и они имеют обратные знаки аналогичным слагаемым в уравнении (24.2).

При необходимости учета различных метастабильных состояний следует поступить в рамках той же процедуры: "уход" электрона из состояний , и в состояния (см. рис. 1) описывается слагаемым с отрицательным знаком – W_ma _a где W_ma есть скорость перехода из состояния а = 2, 3, i на соответствующее метастабильное состояние .

Таким образом, система уравнений (24.1) (24.2) (24.5) и (24.6) полностью определяет кинетику процесса изменения концентрации атомов в состояниях где а =1, 2, 3. При этом достаточно ограничиться рассмотрением трех уравнений (24.2) (24.5) и (24.6), поскольку дляш уравнения (24.1) общее решение очевидно – интегрируя (24.1) с учетом начального условия ₃(t) = ₃(t₀) получаем

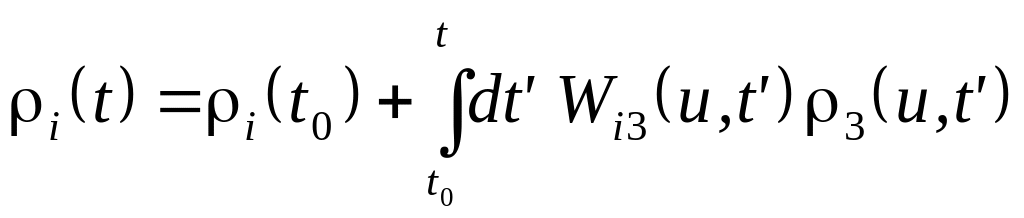(24.7)

Здесь явно введена зависимость интенсивностей пучков света от пространственных координат u = {r, z} где z – ось вдоль пучка света, а r – поперечные координаты.