§21. Методы создания фазового согласования

Условие пространственного синхронизма можно создать несколькими способами. При генерации второй гармоники используют двоякопреломляющие одноосные кристаллы. Одноосный кристалл может быть двух типов: положительный (показатель преломления обыкновенной волны меньше, чем необыкновенной) и отрицательный (показатель преломления обыкновенной волны больше, чем необыкновенной).

Для отрицательного кристалла основная волна, поляризованная как обыкновенный луч (то есть плоскость поляризации волны перпендикулярна оси кристалла), синхронизируется со второй гармоникой ( ) необыкновенной волны (плоскость поляризации лежит в главном сечении, то есть в плоскости, образованной волновым вектором и осью кристалла) путем изменения угла между волновым вектором основной волны и осью кристалла.

Для положительного кристалла ситуация прямо противоположная: условие пространственной синхронизации выполняется для основной необыкновенной волны и обыкновенной волны второй гармоники. Фазовая синхронизация достигается также путем взаимодействия двух основных волн – обыкновенной и необыкновенной – с одной обыкновенной волной второй гармоники (положительный кристалл) или с одной необыкновенной волной (отрицательный кристалл).

Возможны и другие методы создания синхронных взаимодействий. Наиболее выгодным оказывается случай, когда условие выполняется в направлении, перпендикулярном к оси кристалла (поверхности волновых векторов обыкновенной и необыкновенной волны в этом случае касаются). Это расширяет интервал углов для фазового согласования [14].

При генерации третьей гармоники синхронизация осуществляется иным путем. Необходимо выполнить условие: или . В парах металлов это достигается путем добавлении буферного газа. Выбирая подходящий буферный газ и используя его плотность в качестве регулируемой переменной, можно выполнить пространственный синхронизм в следующей форме:

.

(21.1)

На этом пути удалось продвинуться в область вакуумного ультрафиолета ( ), и появилась надежда создать источники когерентного излучения в мягком рентгеновском диапазоне ( ).

22. Параметрические взаимодействия

Генерация оптических гармоник есть частный случай эффекта смешения частот. В приближении заданного поля легко получить амплитуду поля на суммарной частоте. Для этого предположим, что две волны на частотах и фиксированы по амплитуде, тогда из уравнений Максвелла методом, рассмотренным в §18, для третьей волны частоты получим

, (22.1)

где

. (22.2)

Сравнивая (22.1) с (18.8), убедимся, что решение (22.1) будет иметь вид, аналогичный (18.9)

, (22.3)

где амплитуда вынужденной волны

(22.4)

что полностью определяет электродинамику малых преобразований эффектов смешивания частот.

Эффективность преобразования резко возрастает при условии фазового согласования: . В этом случае необходимо исходить из анализа укороченной системы уравнений (18.3).

Рассмотрим процесс параметрического преобразования частоты вверх, несколько отличающийся от эффекта смешения. Пусть частота генерируется путем сложения двух частот и . Однако предположим, что мощность излучения на частоте значительно превосходит мощность на частоте , а первоначальное излучение на частоте отсутствует. Тогда в системе (18.3) уравнение для сводится к тривиальному: , а два других (дополнительно дифференцируя каждое и подставляя одно в другое) примут вид

(22.5)

где

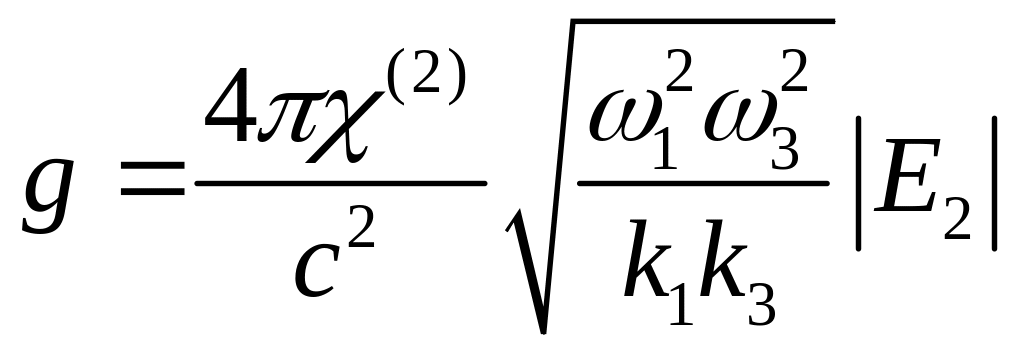. (22.6)

Для принятых граничных условий решение уравнений (22.5) выглядит таким образом:

; (22.7)

.

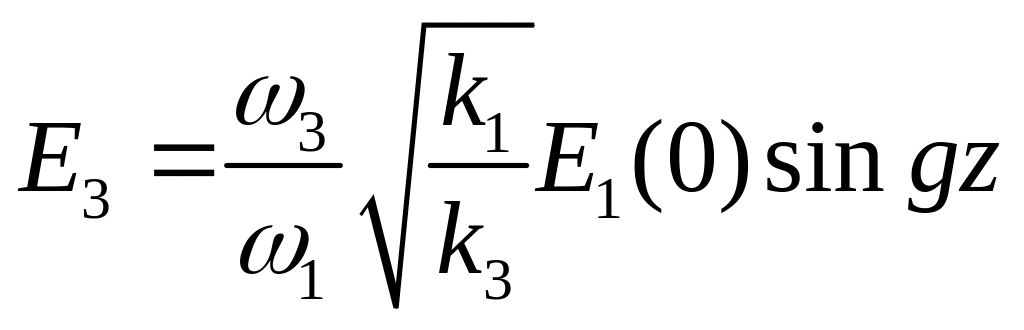Откуда видно, что волна с частотой полностью переходит в волну с частотой на характерной длине .

Далее обратимся к параметрическому усилению и генерации. Из соотношений Мэнли-Роу (18.5) следует, что фотон наибольшей частоты распадается на два фотона меньшей частоты. Таким образом, слабый сигнал на меньшей частоте может быть усилен за счет энергии волны высокой частоты – волны накачки. Возникающая волна разностной частоты – холостая волна – также будет усиливаться. Если организована обратная связь, например, сигнал повторно пропускается через кристалл в нужной фазе (резонатор), то усилитель превращается в генератор, причем самовозбуждение генератора может произойти с затравкой из шумов, когда усиление за один проход превысит соответствующие потери.

Из системы (18.3) следует, что для заданной амплитуды волны накачки поле сигнала и холостой волны определяется из уравнений

(22.8)

где . Дифференцируя еще раз каждое из уравнений и подставляя одно в другое, приходим к системе независимых уравнений второго порядка

;

, (22.9)

где

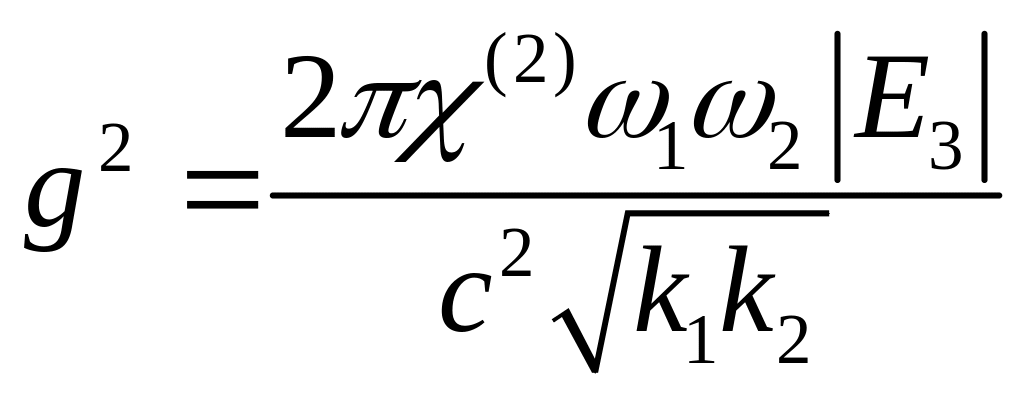. (22.10)

Общее решение (22.9) при имеет вид

, (22.11)

и аналогичное выражение для получаем из (22.11) перестановкой индексов. При имеем , то есть экспоненциальный рост мощности. Для параметрического усиления при взятых выше граничных условиях существуют выражения для сигнала

. (22.12)

и для холостой волны

. (22.13)

В предельном случае ( ), который описывает ситуацию для параметрического генератора, получим

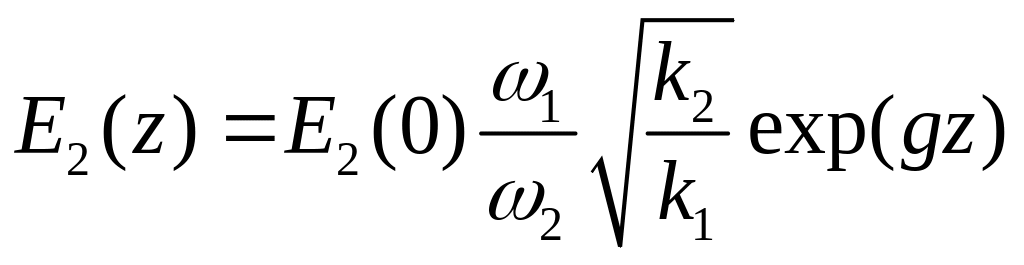(22.14)

Отклонение от условий фазового синхронизма ( ) приводит к уменьшению эффективности параметрического усиления. Характеристическое уравнение для каждого из (22.9) имеет вид

, (22.15)

откуда следует, что существует порог для усиления

. (22.16)

Если учесть потери, то в случае их равенства и при порог параметрического усиления запишется как

, (22.17)

Где – коэффициент поглощения [7].