§17. Общая теория нелинейных восприимчивостей для произвольной квантовомеханической системы

Эволюция произвольной квантовомеханической системы во времени описывается уравнением для матрицы плотности

, (17.1)

где гамильтониан относится к взаимодействию системы с внешним полем. Формальный вывод решения уравнения (17.1) можно получить путем следующего рассмотрения. В дальнейшем удобно использовать новые операторы, которые определяются правилами

; (17.2)

. (17.3)

Это так называемые операторы Лиувилля, действующие согласно этим правилам в пространстве обычных операторов (а не волновых функций), в связи с чем и называются супероператорами. Уравнение для матрицы плотности в этих обозначениях запишется в виде

. (17.4)

Переход к представлению взаимодействия можно совершить, вводя новую матрицу плотности

, (17.5)

для которой уравнение (17.4) преобразуется в

; (17.6)

. (17.7)

Общее решение уравнения (17.6) представляют в виде ряда (в чем легко убедиться непосредственной проверкой):

. (17.8)

Возвращаясь к исходному виду, получим для матрицы плотности общее решение в окончательном виде

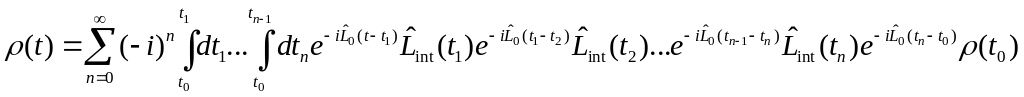. (17.9)

Это решение совместно с общим выражением для средней плотности тока

, (17.10)

В дипольном приближении , где - дипольный момент квантовой системы. Поэтому из (17.10) с учетом (17.9) и формулы (17.3) видно, что наведенный ток представляется в виде ряда по степеням электрического поля.

Если квантовая система замкнута, то супероператор просто определяется через матричные элементы гамильтониана согласно (17.2). Однако в ряде случаев (газ атомов или молекул, парамагнитные ионы в кристалле, оптические центры в твердых телах) квантовая система может быть разделена на две части: малую (подсистема) и большую (резервуар).

В подсистему могут быть включены парамагнитные ионы, которые можно иногда считать изолированными друг от друга, но тем не менее с каждым ионом путем сверхтонкого взаимодействия связано некоторое количество соседних ядер (ион хрома в решетке корунда взаимодействует с ядрами алюминия).

В большую часть – резервуар – включен весь остальной кристалл (или его часть – фононы, магноны и т.д.). Для подсистемы степени свободы во времени меняются в соответствии со взаимодействием отдельных ее частей (ион плюс ядра). Для резервуара степени свободы практически не зависят от наличия подсистемы, так что будем полагать, что резервуар находится в состоянии теплового равновесия.

При таком подходе к вычислению “отклика” среды на внешнее воздействие необходимо знать лишь матрицу плотности подсистемы. Поэтому предварительно проводят усреднение интересующих величин в зависимости от состояния резервуара и тем самым исключают из рассмотрения степени свободы резервуара. Этот подход применяется в теории релаксации [10], и именно с этой целью удобно использовать методику супероператоров.

В общем случае взаимодействие подсистемы и резервуара приводит к перенормировке уровней энергии подсистемы и смешиванию ее состояний. Супероператор для подсистемы не сводится к виду (17.2). Лишь в простых случаях (невырожденные системы, малые взаимодействия) происходит сдвиг уровней подсистемы и появляется экспоненциальное затухание возбужденных состояний. Иными словами, для подсистемы, взаимодействующей с термостатом, справедливо описание с помощью неэрмитового гамильтониана. В общем случае, особенно когда имеет место вырождение уровней, супероператор никакому гамильтониану не соответствует, а имеет сложную структуру.

Для невырожденных систем с затуханием действие супероператора сводится к следующему правилу:

, (17.11)

где , - энергетический спектр подсистемы; , - полуширина энергетического уровня .

В этом случае для монохроматических полей матрица плотности (17.9) принципиально вычисляется до конца. Вычисления носят простой характер, однако сложность и громоздкость окончательных выражений увеличивается с ростом порядка приближения по степени поля. Приведем конечные формулы. В дипольном приближении вместо тока вычисляют макроскопический дипольный момент :

, (17.12)

где - концентрация “центров”; - оператор дипольного момента центров. Подставляя в (17.12) матрицу плотности (17.9) и производя вычисления с учетом (17.11), получаем выражение

, (17.13)

где структура первых трех слагаемых представлена формулами (14.4), (14.6) и (14.7) с учетом тензорного характера восприимчивостей типа (14.8). Восприимчивости первых двух порядков имеют вид:

; (17.14)

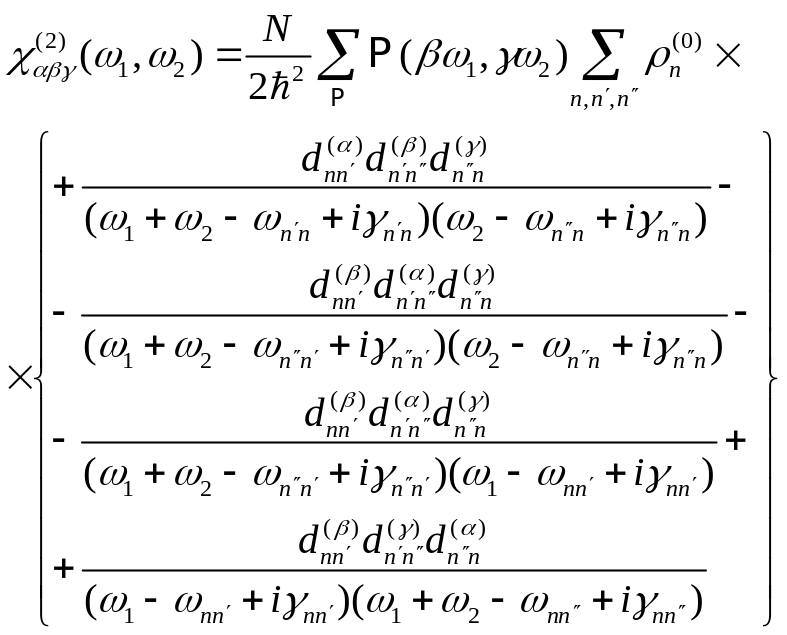. (17.15)

Здесь - операция перестановки величин.

Как видно из последней формулы и из классического результата (16.21), частотная зависимость квантово-механической системы количественно отличается от восприимчивости классической системы, хотя качественно они соответствуют друг другу. Для восприимчивости третьего порядка приведем лишь выражение, ответственное за генерацию третьей гармоники:

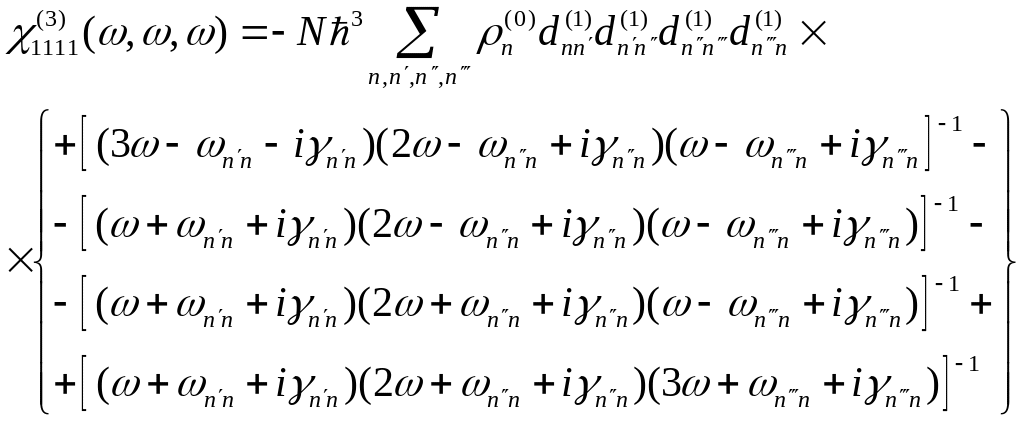. (17.16)

Интересно сравнить классическое выражение (16.23) и последнее (17.16). Оба содержат резонансы при , , (для классики: ). Однако промежуточный резонанс имеет место лишь для квадратичного ангармонизма, который довольно часто отсутствует. Кроме того, видно, что резонанс на основной частоте обладает особенностью третьего порядка для анграмонического осциллятора, тогда как для квантово-механической системы (атом, молекула) эта особенность первого порядка.