§16. Модель ангармонического осциллятора
Для
расчета линейной части поляризации
вещества полезной оказалась модель
гармонического осциллятора,
применяемая в настоящее время при
расчете ионной поляризуемости кристаллов.
Качественно ее можно применять для
оценки электронной поляризуемости. В
этом случае электроны вещества выступают
как гармонические осцилляторы, обладающие
собственными частотами, которые
соответствуют наблюдаемым спектральным
линиям. Переменное электрическое поле,
действуя на оптический электрон, вызывает
вынужденные колебания гармонического
осциллятора. Положим, что
– заряд электрона,
- его масса, а
– собственная частота. Под действием
электрического поля частоты
и амплитуды
электрон отклоняется в сторону действия
поля, а изменение его координаты
во времени описывается уравнением
Ньютона
,
(16.1)
где
- постоянная затухания. Частное решение
уравнения (16.1), описывающего вынужденные
колебании, имеет следующий вид
(16.2)
Таким образом, с каждым электроном связан дипольный момент
.,
(16.3)
где введена функция
,
(16.4)
для которой справедливо условие
Обычно величину
.
(16.5)
называют коэффициентом поляризуемости.
Коэффициент
линейной восприимчивости
связан с коэффициентом поляризуемости,
и эта связь особенно проста для газа
,
(16.6)
где
- число электронов в единице объема.
Для плотной среды она сложнее, но
принципиально ничего не меняется. Если
в атоме, молекуле или элементарной
ячейке кристалла имеется несколько
электронов, обладающих различными
частотами
и число электронов с частотой
есть
,
то вместо (16.5) следует использовать
общую формулу
,
(16.7)
где
(16.8)
Выражения
(16.6), (16.7) описывают зависимость от частоты
линейной восприимчивости
, а, следовательно, диэлектрической
проницаемости
,
коэффициента поглощения “
”
и показателя преломления вещества “
”,
которые определяются формулой
.
Именно таким путем удается объяснить
эффект аномальной дисперсии – зависимость
показателя преломления от частоты,
причем все рассматривается в рамках
классической механики.
Хотя квантовая механика построена на совершенно новых принципах, однако применение ее к данной задаче не меняет качественного описания на основе механики Ньютона. Изменения в основном коснулись количественных характеристик, а именно: выражение (16.7) сохраняет свой вид за исключением того, что собственную частоту необходимо заменить частотой перехода:
,
(16.9)
где
и
- энергетические уровни атома, молекулы
или какой-либо другой квантовой системы.
Число электронов с частотой
также должно быть заменено новым числом
,
(16.10)
Называемым
силой
осциллятора,
которая для этого электрона определяется
вероятностью спонтанного перехода
из состояния
в состояние с энергией
и выражается формулой [5]:
,
(16.11)
то
есть в конечном счете определяется
интенсивностью спонтанного излучения
с соответствующего уровня энергии. Если
в квантовой системе полное число
электронов равно
,
то
.
(16.12)
Например,
для атома водорода при переходе
соответствующая сила осциллятора равна
0,4162. Поскольку
в этом случае
,
то всем остальным переходам, в том числе
и переходам из непрерывного спектра на
уровень
,
соответствует сумма сил осцилляторов,
равная 0,5838.
По мере увеличения амплитуды электрического поля возрастает амплитуда колебаний осциллятора. Особенно сильно это проявляется в условиях, близких к резонансу, в которых уже необходимо учесть ангармонизм колебаний. Поэтому для описания нелинейной части поляризации вещества полезной оказалась модель ангармонического осциллятора. В связи с этим вместо уравнения (16.1) будем иметь
,
(16.13)
где
ангармоничность колебаний учитывается
слагаемыми
и
,
причем каждое последующее слагаемое
дает вклад, значительно меньший
предыдущего:
,
где
- амплитуда колебаний осциллятора.
Если
гармонический осциллятор подвергается
воздействию нескольких переменных
электрических полей, то каждое из полей
действует независимо от другого и
конечная координата осциллятора есть
простая сумма отклонений для каждого
поля в отдельности. Однако эта независимость
уже не имеет места для ангармонического
осциллятора, сколько малыми ни были бы
величины
и т.д.
Пусть
электрон находится в поле двух
электрических волн с частотами
и
и с амплитудами
и
.
Тогда решить уравнения (16.13) можно методом
последовательных приближений, полагая,
что
,
(16.14)
где
Подставляя (16.14) в (16.13) и ограничиваясь
первыми слагаемыми в наинизшем нелинейном
приближении, получим следующую систему
уравнений:
;
(16.15)
;
(16.16)
.
(16.17)
Решение уравнения (16.15) имеет вид, аналогичный (16.2),
(16.18)
Или в более компактной форме
,
(16.19)
где
.
Подставляя (16.19) в уравнение (16.16), получим его решение в следующем виде
,
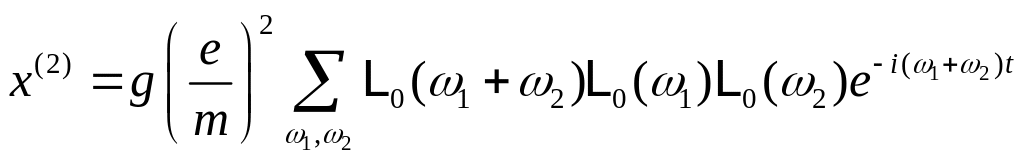(16.20)
где
.
Из (16.20) видно, что ангармонический
осциллятор испытывает колебания на
удвоенный частотах
и
(вторые гармоники), на суммарных и
разностных частотах
(комбинарные частоты), а также имеется
постоянное во времени смещение (эффект
выпрямления). С каждым таким колебанием
связан соответствующий дипольный момент
,
и по аналогии с линейной восприимчивостью
(16.6) можем записать нелинейную
восприимчивость:
.
(16.21)
Заметим,
что
резко возрастает при резонансах
,
,
.
Прохождение через вещество одной волны приводит к эффекту генерации второй гармоники – волны на частоте , и этот процесс будет описываться с учетом (16.4) нелинейной восприимчивостью следующим образом:
.
(16.22)
Аналогичным
путем выводится нелинейная восприимчивость
.
В последнем случае надо рассматривать
взаимодействие трех волн с частотами
и амплитудами
.
Конечный результат имеет вид
,
(16.23)
где
частоты
,
и
принимают значения
.
Из
(16.23) видно, что нелинейная восприимчивость
третьего порядка резко меняется в
следующих резонансных случаях:
.
Рассмотренные особенности изменения нелинейных восприимчивостей и в зависимости от частоты сохраняются и при более правильном расчете на основе квантовой механики. Однако такие расчеты имеют громоздкие формулы [6]. Модель ангармонического осциллятора хорошо описывает нелинейные свойства твердых тел в области инфракрасных частот, где основную роль играют оптические ветви колебаний кристаллов. Нетрудно видеть из вышеприведенных формул, что
.
Аналогичную связь можно найти и для . Полученные и обобщенные результаты распространяются на трехмерный случай [8].