§ 12. Солитоны
Как показано в предыдущем параграфе, при определенных условиях плоская волна становится неустойчивой относительно продольных возмущений. Волна разбивается на отдельные волновые пакеты, которые изменяют свою форму, в частности, испытывают самосжатие. Однако для сильно сжатого волнового пакета существенную роль начинает играть дисперсионное расплывание пакета, имеющее место в обычной линейной оптике. Конкуренция самосжатия и дисперсионного расплывания может привести к стабилизации формы волнового пакета. Возникает устойчивый импульс, который двигается в среде, не изменяя своей формы. Такую уединенную волну называют солитоном. Рассмотрим подробнее формирование такого устойчивого волнового пакета в нелинейной среде.
Будем искать амплитуду волнового пакета в виде
.
(12.1)
В данном случае полагаем, что волна стабилизирована в поперечном направлении и обладает огибающей амплитуды в продольном направлении, нахождение формы которой и является нашей задачей. Подставим (12.1) в нелинейное параболическое уравнение (11.1) и получим
.
(12.2)
Упростим это уравнение. Введем новую переменную
,
И перепишем (12.2) в иной форме, а именно:
;
(12.3)
,
(12.4)
где
.
Уравнение (12.3)
представляет
собой уравнение Ньютона для материальной
точки единичной массы в потенциальном
поле вида (12.4) (рис.5).
Из графиков видно, что имеется два
минимума при
.
Это означает, что плоская волна с такой
амплитудой будет устойчива. Потенциальная
энергия вблизи своего минимума имеет
вид
.
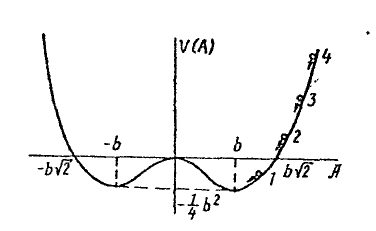
Рис.5. “Потенциальная энергия” образования устойчивых форм волнового “пакета” в нелинейной среде
Откуда
видно, что частота гармонических
колебаний равна
вблизи
.
По мере увеличения амплитуды колебания
становятся все в большей степени
отличными от гармонических, и период
этих колебаний возрастает. Наконец,
имеется особый случай, когда начальное
состояние материальной точки соответствует
,
и она находится в покое. Это положение
неустойчивого равновесия. Малое
возмущение приводит в движение
материальную точку. Она достигает своего
максимального значения
,
где происходит поворот, так что
материальная точка возвращается в
начальное состояние
.
Период такого колебания стремится к
бесконечности.
Эти физические соображения подтверждены точным расчетом. Положим
,
(12.5)
тогда первый интеграл уравнения (12.3) легко находится
.
(12.6)
Это
есть полная энергия материальной точки.
При
и
имеем
.
Далее
.
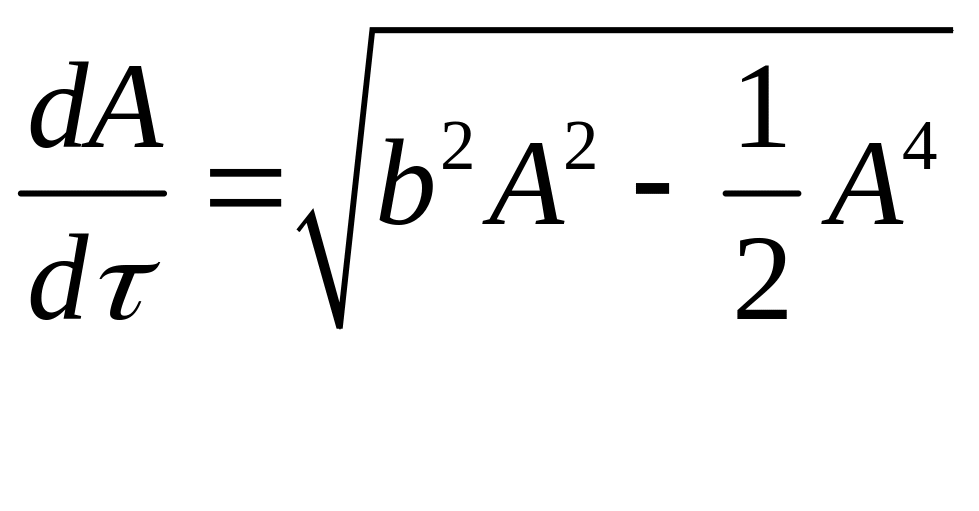Решение принимает вид
при
;
при
,
откуда находим
.
Окончательно преобразуя решение к
прежним переменным, получим
,
(12.7)
при
этом
.
Заметим, что если
при
,
то, как это видно из физической аналогии
с материальной точкой, будут возникать
периодические волны в виде последовательных
импульсов, близких по форме к солитонам
(12.7).