§ 11. Устойчивость плоской волны в нелинейной среде
Запишем нелинейное параболическое уравнение более компактно:
.
(11.1)
В уравнении (11.1) ввели обозначение оператора
Поле волны представим в виде
. (11.2)
Подставим выражение (11.2) в исходное уравнение (11.1) и разделяя мнимые и действительные части, получим
;
(11.3)
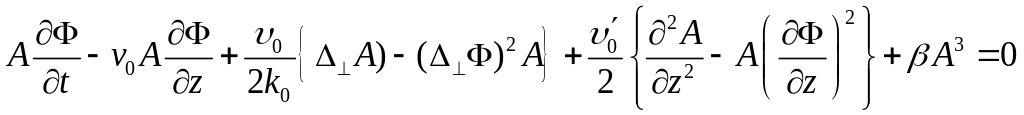. (11.4)
Отметим,
что если пренебречь вторыми производными
в (11.3) и (11.4), то придем к приближению
геометрической оптики, причем для
одномерного случая (
)
эти уравнения совпадают с (9.16) при
определении фазы с точностью до постоянной
величины.
Если
,
- лишь функция времени, то из (11.4) следует,
что
.
Таким
образом, при фиксированной амплитуде
и волновом векторе
частота плоской волны сдвигается и
становится равной
.
Этот эффект можно наблюдать в кольцевом лазере бегущей волны.
Исследуем устойчивость полученного решения. Предположим, что амплитуда и фаза волны имеют малые возмущения, то есть
,
,
Подставим эти выражения в уравнения (11.3) и (11.4) и удержим лишь величины первого порядка по малым возмущениям (то есть проведем линеаризацию уравнений), в результате получим систему
;
(10.5)
.
Делая
вывод, мы использовали явный вид оператора
.
Решение системы (11.5) представим в виде
;
(11.6)
.
Подставляя (11.6) в (11.5), получим дисперсионное уравнение
(11.7)
где
определяется соотношением
.
(11.8)
Из (11.7) находим, что
.
(11.9)
Проведем
анализ полученного результата для
некоторых частных случаев. Пусть
,
что означает отсутствие продольных
(вдоль направления распространения
волны) возмущений. Тогда из (11.8) и (11.9)
видно, что при условии
корень
в (11.9) становится чисто мнимым. Иными
словами, плоская волна становится
неустойчивой в поперечном направлении.
Знак равенства при этом соответствует
порогу самозахвата плоской волны, а
дифракционная расходимость подавляется
самофокусировкой. Если размер пучка
,
то наименьшее
,
поэтому пороговую мощность самозахвата
можно оценить согласно выражению
.
Видно, что пороговая мощность не зависит от размеров поперечного пучка.
Рассмотрим
плоскую волну, устойчивую в поперечном
направлении
.
Из (11.8) следует, что
.
Если
,
то при условии
(11.10)
корень
становится мнимым, то есть волна
неустойчива для продольных возмущений.
В отдельных местах она будет “расползаться”,
а в других – “сгущаться”. Этот эффект
носит пороговый характер, аналогичный
эффекту самофокусировки, при условии,
конечно, что нелинейный коэффициент
.
Для малых
неравенство
(11.10) выполняется со значительным запасом.
Более того, в этом случае имеем
И волна становится неустойчивой при
,
Которое
заведомо выполнялось в предыдущем
случае, но так же и при
и
.
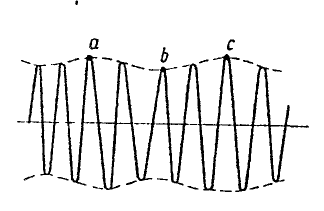
Рис.4. Разбиение монохроматической волны на отдельные волновые “пакеты”
(начальная стадия)
Физика неустойчивости в данном случае следующая: плоская волна, движущаяся в некотором направлении (рис.4), промодулирована по амплитуде в этом же направлении. В точках a (“горбы”) амплитуда поля больше, чем в точках b (“впадины”). Поэтому фазовая скорость на “горбах” больше (при ), чем во “впадинах”. Это приводит к тому, что в интервале (a, b) длина волны начнет уменьшаться, а волновой вектор – возрастать. В интервале (b, c), наоборот, длина волны увеличивается, а волновой вектор уменьшается.
Так как , то групповая скорость пакета волн в интервале (a, b) уменьшается по сравнению с групповой скоростью пакета в интервале (b, c). “Пакеты” начнут отделяться друг от друга, произойдет разбиение плоской волны на отдельные волновые пакеты. При этом в интервале (a, b) фронт волнового пакета становится более крутым, тогда как в интервале (b, c) – более пологим. Возникает вопрос, до каких пор будет происходить такое изменение плоской волны (в продольном и поперечном направлении) и какая волна будет в этом случае устойчивой. Частично не это дается ответ в следующем параграфе.