§ 10. Нелинейное параболическое уравнение
.
Распространение плоских волн и волновых пакетов, близких к плоских волнам, можно описывать параболическим уравнением, вывод которого дается в этом параграфе. Сначала рассмотрим вывод, характеризующей однородную линейную диспергирующую среду, затем обобщим результаты на случай рассмотрения неоднородной среды и далее нелинейной среды в нелинейной оптике.
Предположим, что электромагнитное поле распространяется в изотропном немагнитном диэлектрике. Электрическое поле волны удовлетворяет уравнению Максвелла (6.6). Для определения фурье-компоненты электрического поля и индукции удобно ввести следующие выражения:
(10.1)
В изотропной диспергирующнй линейной среде связь между фулье-компонентами поля и индукции представлена в виде
,
(10.2)
где
постоянная
обозначает диэлектрическую проницаемость,
зависящую от волнового вектора и частоты.
Из уравнения Максвелла (6.6) и из выражений
(10.1) с учетом уравнения
легко получаем
.
(10.3)
Поскольку
,
то из (10.3) следует хорошо известное
дисперсионное уравнение
,
которое
определяет функцию
,
причем для изотропной среды частота
зависит от величины волнового вектора,
а не от его направления:
.
Фиксированному значению
соответствует определенная
некоторой плоской
волны.
Предположим,
что фурье-компонента
отлична от нуля в окрестности точки
,
то есть волновой пакет, близкий к плоской
волне с заданными параметрами. Введем
обозначение
и перепишем (10.3) в виде
,
(10.4)
откуда следует, что
.
(10.5)
Функцию
представим как ряд
,
(10.6)
где
– значение функции
в
,
а индекс ноль у производных означает,
что они берутся в той же точке.
Рассмотрим
значение
,
близкое к
.
Введем обозначение
тогда
,
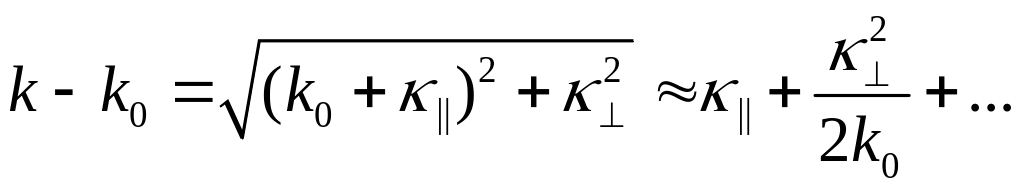(10.7)
где
- проекция вектора
на направление вектора
,
а
- проекция
на нормальное к вектору
направление. Производные в (10.6) представляют
собой групповую скорость пакета, именно
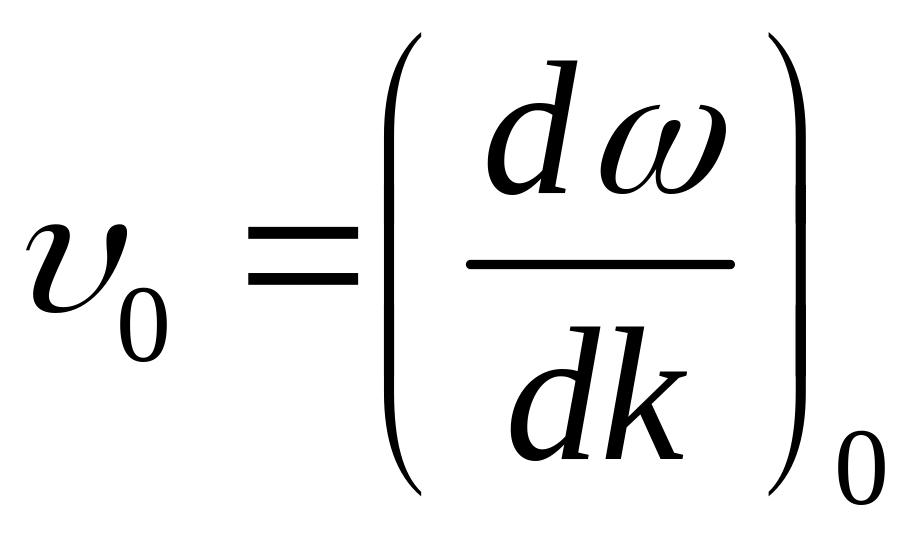
и ее производную
.
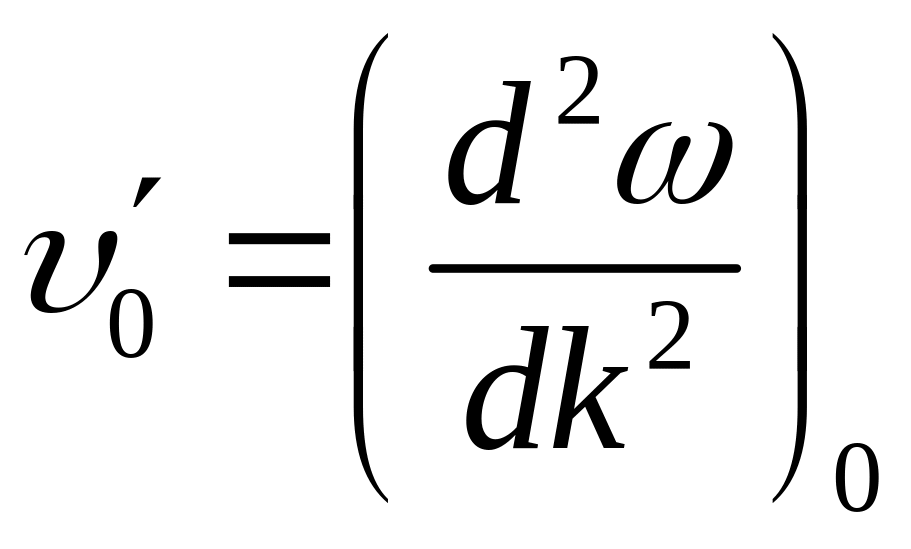Подставим (10.7) в (10.6) и ограничимся членами второго порядка малости. Тогда уравнение (10.5) примет вид
.
Далее выполним обратное фурье-преобразование
(10.8)
И в результате придем к линейному параболическому уравнению:
.
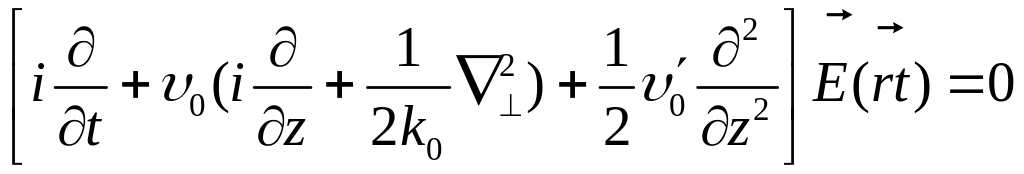(10.9)
Здесь
представляет собой медленно меняющуюся
амплитуду плоской монохроматической
волны с частотой
и волновым вектором
(в соответствии с преобразованием
(10.8);
;
ось
направлена вдоль вектора
.
Обобщим полученное уравнение для неоднородной среды. Часто неоднородную среду можно описать электрической проницаемостью, зависящей от координаты и времени . Необходимо лишь соблюсти требование: изменение параметров среды – ее плотности, температуры, населенности уровней и т.д. – должно происходить медленно, за период колебания волны или на расстояниях порядка длины волны, то есть эффекты временной и пространственной дисперсии должны быть несущественными. Для волновых пакетов, близких к плоским волнам, дисперсией всегда можно пренебречь, за исключением некоторых резонансных ситуаций (когда спектральная ширина “пакета” сравнивается с шириной резонансного уровня в среде). Поэтому диэлектрическую проницаемость неоднородной среды запишем как
,
где
- некоторое среднее значение диэлектрической
постоянной. Тогда вместо (10.5) будем иметь
,
(10.10)
где
первое слагаемое описывает поле в
однородной среде с диэлектрической
постоянной
,
а второе учитывает отклонение от
однородности в среде. Уравнение (9.10)
справедливо в случае
.
Обратное Фурье-преобразование приводит
нас к уравнению
.
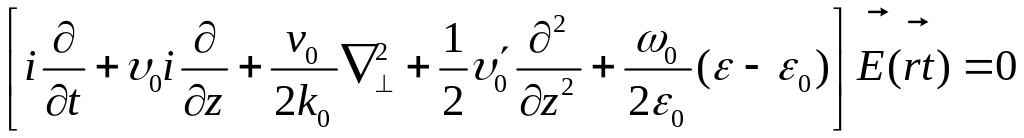(10.11)
Как видно из (10.8), получение параболический уравнений (10.9) и (10.11) с помощью фурье-преобразований сводится к заменам
,
,
.
Предположим, что световая волна линейно поляризована, тогда из (10.11) видно, что поляризация сохраняется при движении волны в среде. Поэтому выберем ось вдоль поляризации и будем рассматривать лишь величины поля. Далее в уравнении (10.10) перейдем к новой переменной
.
В этом случае (10.10) преобразуется в уравнение
,
(10.12)
в которое введены обозначения
;
;
;
.
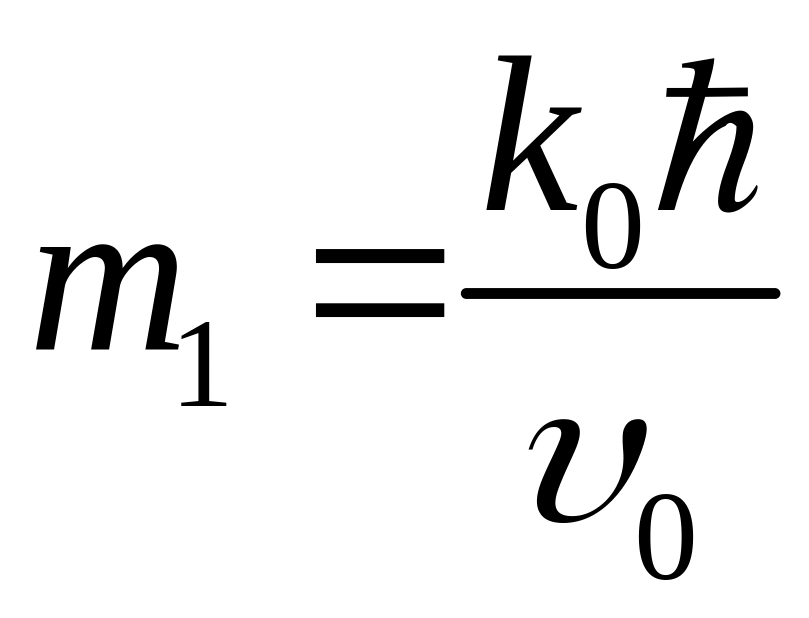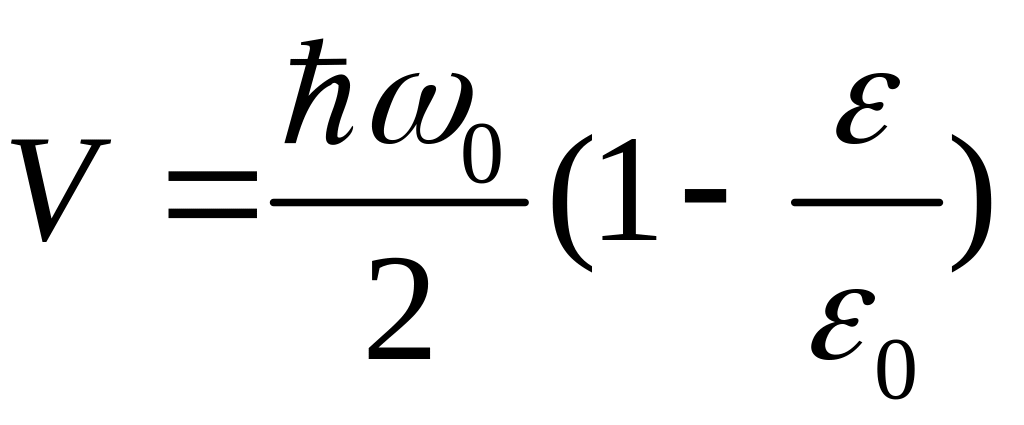(10.13)
Полученное уравнение есть уравнение Шредингера для описания частицы в потенциальном поле. Частица имеет различные массы (эффективный тензор масс) в зависимости от направления. Такие квазичастицы изучаются в разделе физики твердого тела и физики полупроводников для описания носителей тока в кристаллической решетке, экситонных и примесных состояний. Таким образом, амплитуда волнового пакета в неоднородной среде и волновая функция для частицы в потенциальном поле в квантовой механике аналогичны.
Теперь
нетрудно перейти к случаю нелинейных
сред, когда диэлектрическая проницаемость
зависит от электрического поля волны.
Поскольку огибающая волнового пакета
является функцией координат и времени,
то нелинейная среда будет неоднородной.
Поэтому в нелинейной среде параболическое
уравнение примет тот же вид (10.11) или
(10.12), где вместо
необходимо иметь
.
Например, для слаболинейной среды
зависимость диэлектрической проницаемости
от поля представлена как в (8.1), и поэтому
нелинейное параболическое уравнение
принимает форму:
.
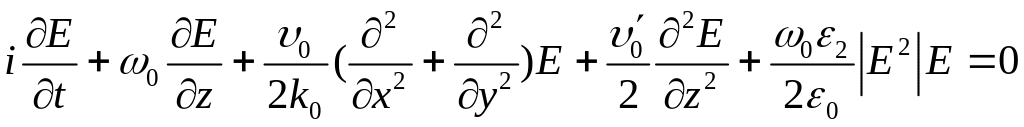(10.14)
Если воспользоваться обозначениями (10.13), то (10.14) можно представить в виде
,
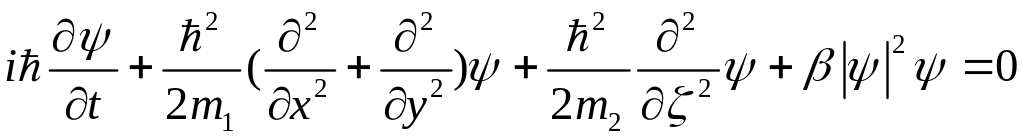(10.15)
где
.
В стационарном случае последнее уравнение
совпадает с уравнением Гинзбурга-Ландау
в феноменологической теории
сверхпроводимости [12].